Теория ядерных реакторов. Семинар к курсовому проекту по спецкурсу № 2

*
Тема занятия 2
Сечения взаимодействия нейтронов с ядрами, длина пробега нейтронов, коэффициент воспроизводства топлива

*
Понятие сечения
Ядерное эффективное сечение, эффективное сечение ядра, ядерное сечение реакции, микроскопическое сечение реакции — величина, характеризующая вероятность взаимодействия частицы с ядром.
Единица измерения эффективного сечения — барн (1 барн = 10-28 м²). С помощью известных эффективных сечений вычисляют скорости ядерных реакций или количества прореагировавших частиц.
Эта величина имеет физический смысл подобный смыслу сечения в классической механике, где эффективное сечение определяется как площадь поперечного сечения такой области пространства около частицы-мишени, при пересечении которой бомбардирующей частицей-точкой со 100 % вероятностью возникает взаимодействие.
Однако, ядра атомов и ядерные частицы (α-, β-, γ-частицы, нейтроны и другие частицы) обладают квантовыми свойствами и поэтому сечение реакции характеризует лишь вероятность взаимодействия частицы с ядром.

*
Понятие сечения
Эффективные сечения определяются не геометрическими размерами частиц и ядер, а их квантово-механическими (волновыми) свойствами.
При взаимодействии с ядрами область локализации взаимодействующей с ядром частицы имеет размер порядка дебройлевской длины волны λ и сечение взаимодействия ~π⋅λ2. Поскольку λ обратно пропорционально импульсу частицы, то сечение возрастает по мере уменьшения скорости частицы. Это общая тенденция зависимости сечения от скорости (энергии частицы).
При взаимодействии ядра-мишени и налетающей частицы возможно образование связанных состояний (составных ядер). Однако, для образования такого ядра необходимо чтобы энергия ядра-мишени и налетающей частицы соответствовала бы одному из энергетических состояний составного ядра.

*
Понятие сечения
Это обстоятельство приводит к сложной (резонансной) структуре взаимодействия частиц с ядрами. На рисунке показана зависимость сечения деления σf для 239Pu от энергии в эВ.

Длина пробега нейтронов
Длина свободного пробега нейтронов является случайной величиной и распределена по экспоненциальному закону с плотностью распределения
Эта функция нормирована на единицу. Поэтому средняя длина пробега нейтрона до первого взаимодействия с ядром определяется соотношением

*

Актиноиды
Нас в этой таблице интересуют некоторые актиноиды
В частности торий, протактиний, уран, нептуний и плутоний. Они участвуют в воспроизводстве топлива.

Воспроизводство ядерного топлива
Воспроизводство ядерного топлива - это процесс образования в реакторе вторичных делящихся нуклидов из нуклидов, которые не делятся на тепловых нейтронах. В реакторах, работающих на уране, помимо выгорания делящегося нуклида 235U при радиационном захвате нейтронов ядрами 238U (реакция (n, γ)) образуются ядра нового делящегося нуклида 239Pu. Затем, в результате последовательных захватов на 239Pu образуются также ядра 240Pu и 241Pu. Аналогично в ядерном реакторе, содержащем в активной зоне торий 232Th в качестве сырьевого нуклида, образуется новый делящийся нуклид 233U.
Таким образом, имеется возможность организовать в ядерных реакторах два цикла воспроизводства ядерного топлива, основанных на двух типах ядерных реакций: уран- плутониевый топливный цикл и торий – урановый топливный цикл.
*

Рассмотрим упрощённую схему взаимодействия, которая, строго говоря, не отвечает действительности, однако позволяет получить очень важное соотношение, связывающее скорость взаимодействия и эффективное сечение. Пусть на тонкую мишень (ядра мишени не перекрывают друг друга) падает перпендикулярно поверхности пучок монохроматических нейтронов. Плотность нейтронов в пучке есть n, нейтр/см3, a их скорость v, см/c. Будем рассматривать нейтроны как корпускулы (т. e. длина волны нейтрона много меньше радиуса ядра). В этом случае «столкновение» нейтрона c ядром произойдет только тогда, когда он попадет в плоскость сечения ядра. Если сечение ядра обозначить δ, то в 1 c c ядром будут сталкиваться те нейтроны, которые заключены в объеме vδ. Это число равно nvδ. Полное число взаимодействий («столкновений») в единцу времени в единице объема мишени, содержащей в 1 см3 N ядер,
R = δnvN (1)
*

Простая геометрическая трактовка сечения, использованная при выводе выражения, удовлетворительно согласуется c экспериментом только при больших энергиях нейтронов, когда сечения взаимодействия нейтронов c ядрами имеют значения, примерно равные геометрическому сечению ядра (10-24 см2 для тяжелым ядер). Подтверждением этого факта является подобие сечений для быстрых нейтронов при переходе от ядра к ядру и очень слабое их изменение c энергией. Сечения взаимодействия нейтронов других энергий сильно изменяются при переходе от ядра к ядру c изменением их энергии. Поэтому говорят об эффективном сечении взаимодействия нейтронов c ядрами, которое определяет вероятность протекания процесса и не связано c геометрическими размерами ядра. Большинство сечений ядерных реакций имеют значения от 10-27 до 10-23 см2, т. e. порядка геометрических сечений ядер. Однако есть реакции, сечения которых много больше геометрических сечений ядра (примерно 10-18 см2), a есть реакции (например, реакции под действием медленных заряженных частиц), имеющие сечения много меньше геометрических сечении ядер.
Будем облучать мишень, содержащую N, ядер i-го сорта в единице объема (в дальнейшем для N, будем использовать термин ядерная плотность), пучком нейтронов c плотностью n и скоростью v. Тогда Ri — число реакций i-го типа, происходящих в единице объема мишени в единицу времени, будет пропорционально N, и nv, т. e.
Ri = σiϳNinv (2)
Из сказанного выше и сопоставления выражений (2) и (1) ясно, что σiϳ имеет размерность площади и физический смысл эффективного сечения ядра:
σiϳ=Ri/(Ninv) (3)
Чаще используют термин ядерное или микроскопическое сечение реакции.
*

В зависимости от вида взаимодействия рассматривают различные сечения и вводят соответствующие обозначения. Сечения процессов, не приводящих к изменению структуры ядра, объединяют в сечение рассеяния σs. Оно включает в себя следующие сечения: σp— потенциального рассеяния; σr — резонансного рассеяния; σm —неупругого рассеяния. Итак, σs=σp+σr+σm. Для процессов, связанных только c упругим рассеянием, вводят сечение упругого рассеяния σs=σp+σr. Сечение образования составного (компаунд) ядра обозначают σcomp. Сечения различных каналов распада составного ядра, не связанные c появлением нейтронов, объединяют в сечение поглощения σa. Приведем обозначения сечений для наиболее характерных каналов распада составного ядра: σс — радиационного за-хвата (n, γ); σf — деления (п, f) ; σ2n— реакции (n, 2n) , σα —реакции (n, α).
Для рассмотрения всех процессов взаимодействия нейтрона c ядром вводят полное сечение σt. Оно равно сумме всех парциальных сечений. Используя ранее введенные обозначения, его можно представить в виде суммы только двух сечений
σt=σp+σcomp
Для подавляющего большинства ядер в интервале энергий (10-3-107) эВ
σt=σs+σα
*

МАКРОСКОПИЧЕСКИЕ СЕЧЕНИЯ
Макроскопическое сечение ∑iϳ i-го процесса для ϳ-го нуклида в среде можно определить как произведение i -го микроскопического сечения ядра этого нуклида σiϳ и ядерной плотности j-го нуклида Nϳ:
∑iϳ= Nϳ σiϳ (4)
Используя (3), можно дать другое определение макроскопического сечения ∑iϳ , — это число взаимодействий i-го типа в единицу времени в единице объема j-гo нуклида при единичном nv.
Ядерную плотность определяют по формуле
Nϳ=NAp/Mi (5)
Если вещество представляет собой гомогенную смесь различных ядер, то макроскопическое сечение смеси определяют, как сумму сечений
∑icм=∑∑iϳ
*

Ядерная плотность j-го компонента может быть легко определена, если задана его массовая концентрация c , и плотность смеси pcm:
*

При гетерогенном расположении материалов необходимо учитывать объемную долю, занятую данным веществом . Тогда ядерные плотности каждого вещества N , домножают на ωi:
Необходимо помнить, что в случае гетерогенного расположения материалов сечение не всегда определяют как сумму сечений (1.9.6), так как различные материалы находятся в разных условиях.
*

Ядерное топливо, содержащее в качестве делящегося компонента 235U, называют первичное ядерное топливо, ядерное топливо, содержащее в качестве делящегося компонента 239Pu или 233U, называют вторичное ядерное топливо.
Если вторичный делящийся нуклид отличается от выгорающего, то процесс называют конверсией (превращением), а реактор- конвертором. Если вторичный нуклид совпадает с первичным, то процесс называют воспроизводством или бридингом.
Интенсивность процесса воспроизводства ядерного топлива в реакторе характеризуется коэффициентом воспроизводства КВ, хотя при процессе конверсии урана в плутоний его было бы правильнее называть коэффициентом конверсии (КК). Существует несколько определений КВ.
Для характеристики процесса воспроизводства в данный момент времени (при данной глубине выгорания) вводится дифференциальный коэффициент воспроизводства, равный отношению скорости образования ядер вторичного топлива dNвт/dt к скорости выгорания ядер dNвыг/dt :
КВ, диф = (÷dNвт/dt ÷)/(÷dNвыг/dt÷) = dNвт/ dNвыг (5.9а)
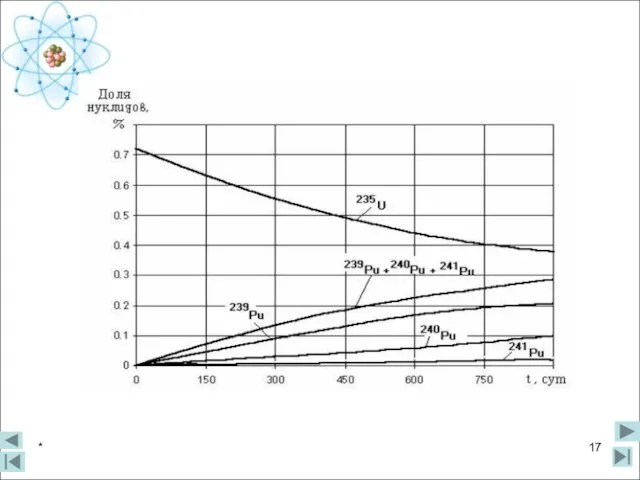
На рис. 5.2 приведены кривые накопления изотопов Pu и выгорания 235U в реакторе на природном уране с глубиной выгорания примерно ~ 4500 Мвт´сут/т=4,5Мвт´сут/кг. Видно, что дифференциальный КВ непрерывно изменяется в процессе выгорания топлива, поскольку представляет собой отношение производных двух кривых.
*

*