Содержание
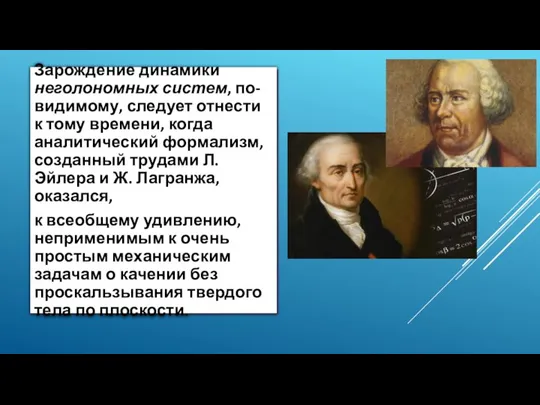
- 2. Зарождение динамики неголономных систем, по-видимому, следует отнести к тому времени, когда аналитический формализм, созданный трудами Л.
- 3. Только в 1894 г. в книге «Принципы механики, изложенные в новой связи» (через 106 лет после
- 4. . К настоящему времени динамика неголономных систем оформлена как самостоятельная часть общей динамики механических систем-находит широкое
- 5. Условия голономные и неголономные. Условия (они же ограничения), накладываемые на движение механической системы разделяют как потенциальные:
- 6. Условия голономные и неголономные. Задача учета кинематических связей в нелинейном виде не разработана, в линейном виде
- 7. Условия голономные и неголономные. Если дифференциальную связь (3) нельзя записать как полный дифференциал некоторой функции То
- 8. Метод составления уравнений динамики механической системы при наложении различных типов условий на переменные (2) а1 [
- 9. Методы составления уравнений динамики механической системы при наложении различных типов условий на переменные (2) а1 [
- 10. Однако, способ уменьшения числа переменных вводя кинематические условия как новые переменные давно предложен А. Пуанкаре и
- 11. Указанное выражение получается совершенно естественно при вычислении вариации интеграла действия Гамильтона. В современных обозначениях: dΩ =d[x1]⋀d[x]-d[H]⋀d[t]
- 12. НОВЫЙ МЕТОД Поскольку из этого дифференциального инварианта следует система уравнений движения - любой механической системы, а
- 13. В случае использования интегрального инварианта механики по Картану, введение ограничений на переменные механической системы (как голономные,
- 14. Применение нового метода к составлению уравнений динамики волнового твердотельного гироскопа ( по В.Ф. Журавлеву, Д.М. Климову)
- 15. L=1/2 ((v1+(R-w) Ω)2+(w1+v Ω)2)- 1/2 κ12 (wss+vs )2- -(1/2 ) δ12 (vs -w)2 при наложении условия
- 16. . Если пренебречь потенциальной энергией, то эффект инертных свойств упругой деформацией гибкого кольца следует из оставшейся
- 17. Анализ приближений условий нерастяжимости средней линии на основе НОВОЙ формы нерастяжимости: vs+R-w-> R Cos[Q],-ws-v-> R Sin[Q]
- 18. Эффект инертных свойств упругой деформацией гибкого кольца следует из уравнений кольца и в случае когда потенциальной
- 19. Уравнение динамики для переменных гибкого кольца эквивалентно : 1/2 d[Ω2 rψ2+Ω2 vψ2]-((R+r)2+v2) d[Ω2/2]=0 или ((R+r)2+v2) d[Ω2/2]=1/2
- 20. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Картан Э.Д. Интегральные инварианты М.: 1922 г. 2. Суслов Г.К. Теоретическая механика,
- 22. Скачать презентацию
















![Уравнение динамики для переменных гибкого кольца эквивалентно : 1/2 d[Ω2 rψ2+Ω2 vψ2]-((R+r)2+v2)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1067866/slide-18.jpg)

 Необыкновенные оптические явления
Необыкновенные оптические явления Konsultatsia_2 (1)
Konsultatsia_2 (1) Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью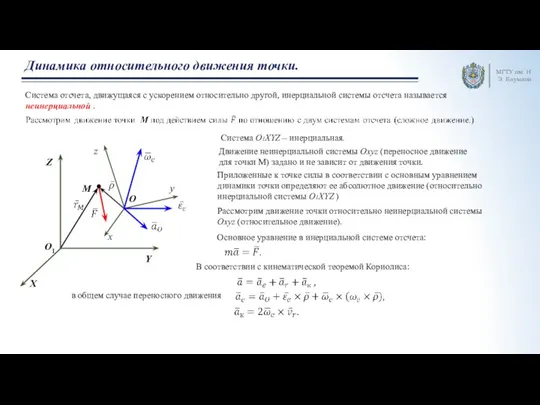 Динамика относительного движения точки. Лекция 2
Динамика относительного движения точки. Лекция 2 Решение задач
Решение задач Tema_4_Para_sil_i_moment_sil_otnositelno_tochki_Ploskaya_sistema_proizvolno_raspolozhennykh_sil
Tema_4_Para_sil_i_moment_sil_otnositelno_tochki_Ploskaya_sistema_proizvolno_raspolozhennykh_sil Постоянный электрический ток. Повторение
Постоянный электрический ток. Повторение История автомобилей
История автомобилей Что изучает физика. Наблюдения и опыты
Что изучает физика. Наблюдения и опыты Электричество. Постоянный электрический ток
Электричество. Постоянный электрический ток Расчёт расхода электроэнергии
Расчёт расхода электроэнергии Линзы. Глаз как оптическая система. Оптические приборы
Линзы. Глаз как оптическая система. Оптические приборы Самоіндукція. Індуктивність. Енергія магнітного поля
Самоіндукція. Індуктивність. Енергія магнітного поля Моделирование термодинамических ансамблей
Моделирование термодинамических ансамблей Уроки физики в 9 , 11 классах
Уроки физики в 9 , 11 классах Молекулярная физика. Основные положения МКТ
Молекулярная физика. Основные положения МКТ Сообщающиеся сосуды
Сообщающиеся сосуды Элемент Вольта
Элемент Вольта Работа и мощность
Работа и мощность Физика атомного ядра
Физика атомного ядра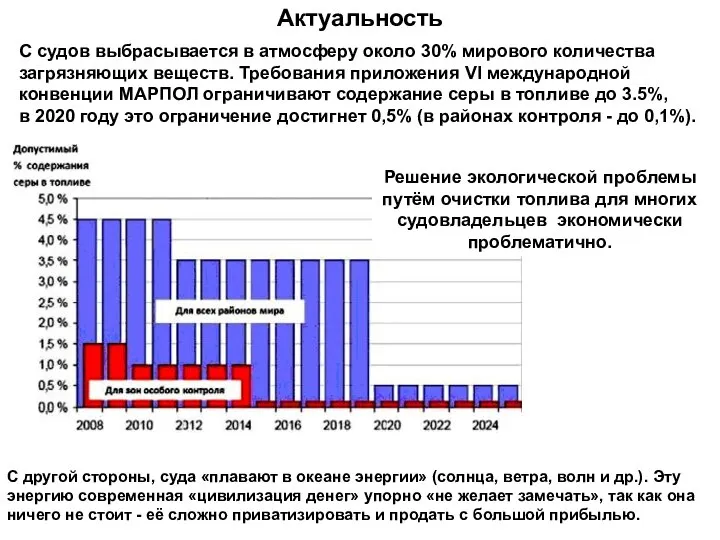 Поиск эффективных способов преобразования энергии морских волн в энергию поступательного движения судна
Поиск эффективных способов преобразования энергии морских волн в энергию поступательного движения судна Плазма и её использование
Плазма и её использование Физика сварочных процессов
Физика сварочных процессов Закон Ома для участка цепи. Расчет сопротивления проводника
Закон Ома для участка цепи. Расчет сопротивления проводника Методика измерения массовой концентрации общего фосфора и фосфора фосфатов в пробах питьевых, природных и сточных вод
Методика измерения массовой концентрации общего фосфора и фосфора фосфатов в пробах питьевых, природных и сточных вод Соединение конденсаторов
Соединение конденсаторов Мобильный телефон с точки зрения физики
Мобильный телефон с точки зрения физики Электрический ток в растворах и расплавах электролитов
Электрический ток в растворах и расплавах электролитов