Содержание
- 2. Учебные вопросы: №1 Метод Законов Кирхгофа; №2 Метод Контурных токов; №3 Метод наложения; №4 Эквивалентные преобразования
- 3. Сложные (разветвленные) цепи содержат большое число ветвей, соединенных между собой в узлах и образующих контуры. Ветвью
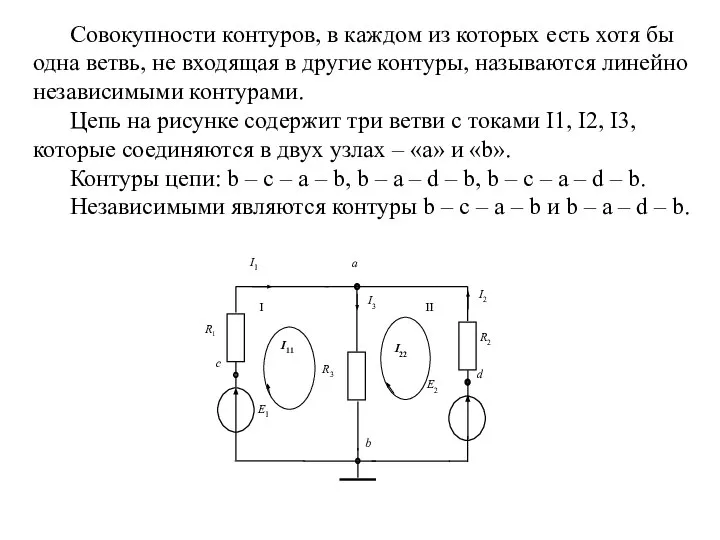
- 4. Совокупности контуров, в каждом из которых есть хотя бы одна ветвь, не входящая в другие контуры,
- 5. Расчеты разветвленных цепей основываются на двух законах Кирхгофа.
- 6. Первый закон Кирхгофа относится к узлам цепи: Алгебраическая сумма токов в узле равна нулю. Или сумма
- 8. Метод контурных токов При использовании метода контурных токов уравнения составляют только по второму закону Кирхгофа для
- 9. Метод контурных токов. Пример. Произвольно выбираем направления обхода контуров по часовой стрелке. Составляем систему уравнений по
- 10. Метод наложения Для линейных электрических цепей справедлив принцип наложения. Его физический смысл состоит в том, что
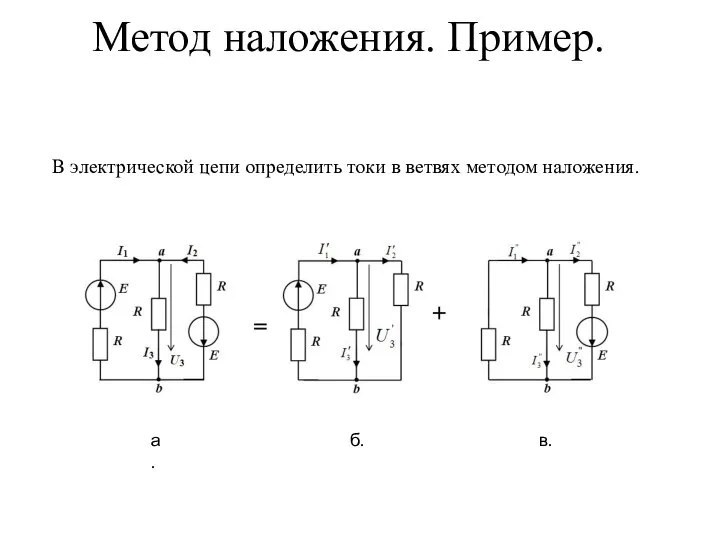
- 11. Метод наложения. Пример. В электрической цепи определить токи в ветвях методом наложения. а. б. в.
- 12. Метод наложения. Пример. 1. Определяем токи в схеме (рис. б) при действии только источника ЭДС Е1
- 13. B; Метод наложения. Пример. 2. Определяем токи (рис. в) при действии источника ЭДС Е2 (Е1 =
- 14. Метод наложения. Пример. 3. Определяем токи в исходной схеме как алгебраическую сумму частичных токов (рис. а):
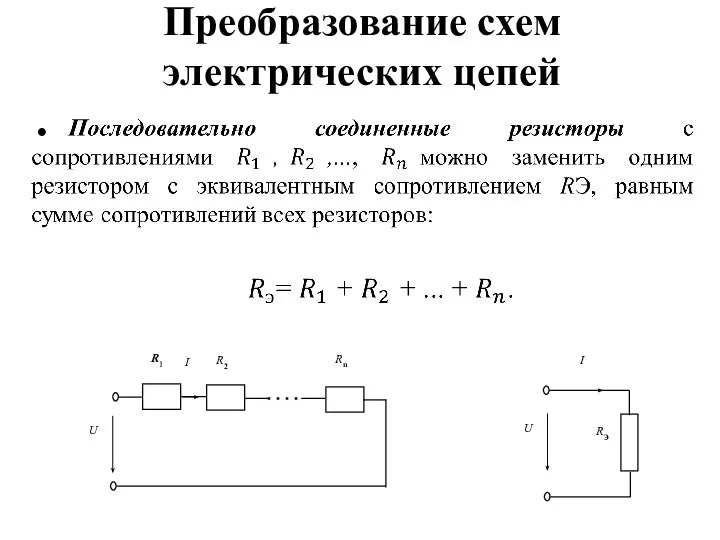
- 15. Преобразование схем электрических цепей
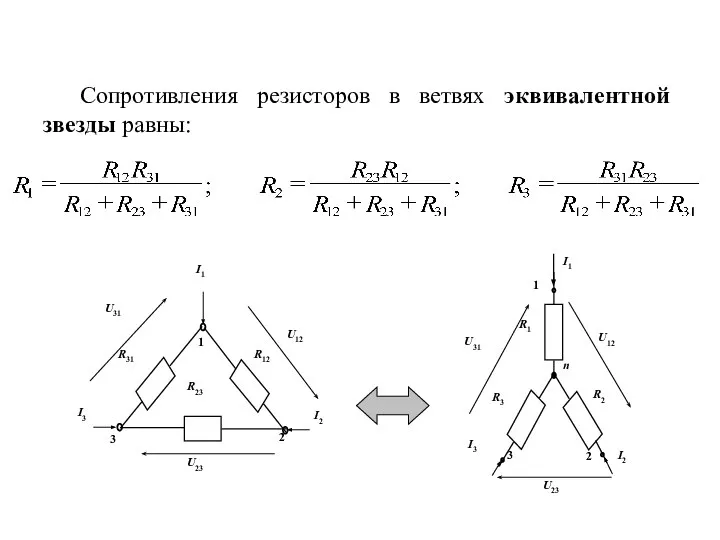
- 18. Сопротивления резисторов в ветвях эквивалентной звезды равны:
- 19. Рассмотрим преобразование “треугольника” в “звезду”. Для “треугольника” запишем уравнение баланса напряжений (второй закон Кирхгофа):
- 20. Напряжение между выводами a и b (разность потенциалов) в схеме “треугольник”: Напряжение между выводами a и
- 23. Скачать презентацию
















 Циклы углов и первый импульс как пророк. Циклы по цене и цели
Циклы углов и первый импульс как пророк. Циклы по цене и цели Иллюзии и Физика. Вечная Борьба
Иллюзии и Физика. Вечная Борьба История нанотехнологий. Лекция 2
История нанотехнологий. Лекция 2 Основные и дополнительные средства защиты в сетях напряжением выше 1000 в
Основные и дополнительные средства защиты в сетях напряжением выше 1000 в ШВЕЙНАЯ МАШИНА
ШВЕЙНАЯ МАШИНА Спектроскопические методы анализа
Спектроскопические методы анализа Технологическая планировка моторного участка ремонта автомобиля АРП
Технологическая планировка моторного участка ремонта автомобиля АРП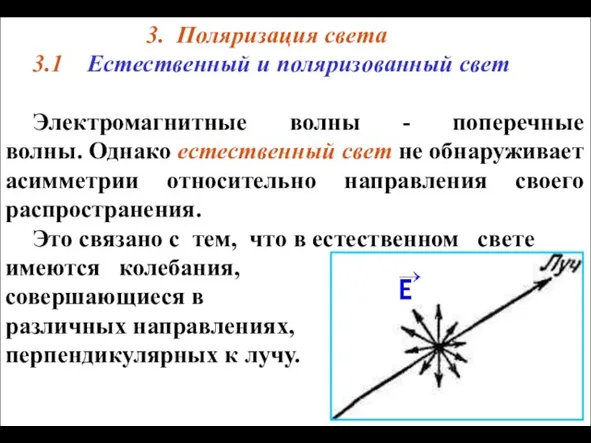 Поляризация света
Поляризация света Природа звука (1)
Природа звука (1) Отчет: Деятельностный подход к преподаванию физики, как средство повышения качества образования
Отчет: Деятельностный подход к преподаванию физики, как средство повышения качества образования Устройство и принцип работы дизельного двигателя
Устройство и принцип работы дизельного двигателя Презентация на тему Влияние электромагнитного поля на организм человека
Презентация на тему Влияние электромагнитного поля на организм человека  Презентация на тему Телескоп
Презентация на тему Телескоп  Простые механизмы, КПД простых механизмов
Простые механизмы, КПД простых механизмов Распространение теплоты в однородных материалах. Теплопроводность однослойной и многослойной плоских стенок. (Занятие 9)
Распространение теплоты в однородных материалах. Теплопроводность однослойной и многослойной плоских стенок. (Занятие 9) Презентация на тему Звуковые колебания и волны
Презентация на тему Звуковые колебания и волны  Принцип Гюйгенса-Френеля
Принцип Гюйгенса-Френеля Кинематика материальной точки
Кинематика материальной точки Производительность карбюраторного и инжекторного двигателя
Производительность карбюраторного и инжекторного двигателя Механическое движение. Скорость. Единицы скорости
Механическое движение. Скорость. Единицы скорости Расчет стоимости электрической энергии
Расчет стоимости электрической энергии Квантовая механика
Квантовая механика Операторы
Операторы Изменение агрегатного состояния веществ
Изменение агрегатного состояния веществ Организация участковой системы ведения путевого хозяйства на западно-сибирской железной дороге
Организация участковой системы ведения путевого хозяйства на западно-сибирской железной дороге Физика для химиков. День второй. Все еще термодинамика
Физика для химиков. День второй. Все еще термодинамика Испарение. Насыщенный пар и его свойства. Влажность воздуха
Испарение. Насыщенный пар и его свойства. Влажность воздуха Отчет о прохождении производственной практики
Отчет о прохождении производственной практики