Модели колебаний (лекция 7)

Затухающими являются колебания, происходящие в диссипативной колебательной системе. В реальной колебательной системе имеются силы сопротивления (трения), действие которых уменьшает энергию колебаний.
При небольших скоростях движения в среде
сила сопротивления пропорциональна скорости:
где r − коэффициент сопротивления среды, [r] = кг/с.
Знак минус в формуле показывает, что сила и скорость имеют противоположные направления.

Уравнение движения (второй закон Ньютона) при наличии квазиупругих сил и сил сопротивления имеет вид:
Обозначения: ;
β – коэффициент затухания колебаний; [β] = 1/с
ω0 – собственная циклическая частота колебаний системы (частота, с которой происходили бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0).

Дифференциальное уравнение свободных затухающих колебаний примет вид:
Общее решение этого уравнения имеет вид:
− циклическая частота затухающих колебаний.
Начальные амплитуда А0 и фаза α определяются из начальных условий: х(0) = х0; υ(0) = υ0.

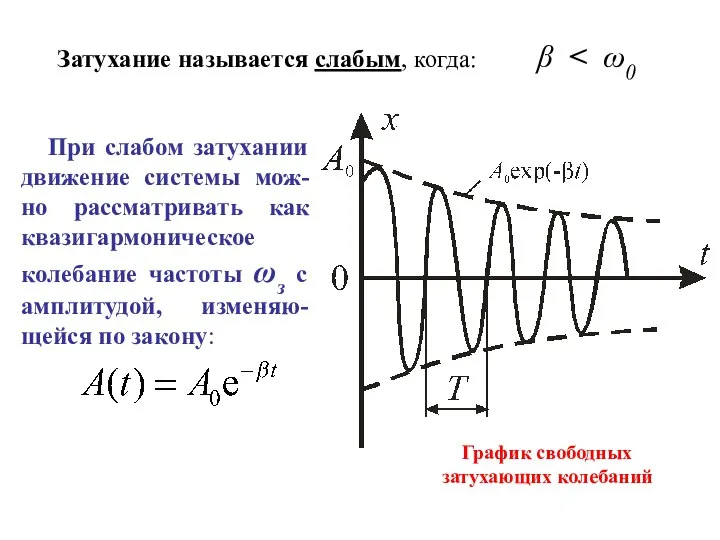
Затухание называется слабым, когда: β < ω0
При слабом затухании движение системы мож-но рассматривать как квазигармоническое колебание частоты ωз с амплитудой, изменяю-щейся по закону:
График свободных
затухающих колебаний

Характеристики затухания
1. Коэффициент затухания колебаний β характеризует скорость затухания колебаний:
2. Время релаксации τ – время, за которое амплитуда колебаний уменьшается в е ≈ 2,7 раз:
откуда βτ = 1, или:
Физический смысл коэффициента затухания колебаний:
это величина, обратно пропорциональная времени,
за которое амплитуда колебаний уменьшается в е раз.

3. Период затухающих колебаний:
4. Декремент затухания – отношение значений амплитуд, соответствующих моментам времени, отличающимся на период:
5. Логарифмический декремент затухания θ –
натуральный логарифм от декремента затухания:
θ

За время τ система успевает совершить число колебаний, равное:
Физический смысл логарифмического декремента затухания − это величина, обратная числу колебаний, совершаемых за время релаксации τ (за время уменьшения амплитуды в е раз):
6. Добротность Q системы – безразмерная величина, обрат-но пропорциональная потерям энергии в колебательной системе.
θ
Q = π/θ
Для идеальной системы (без затухания колебаний): Q → ∞

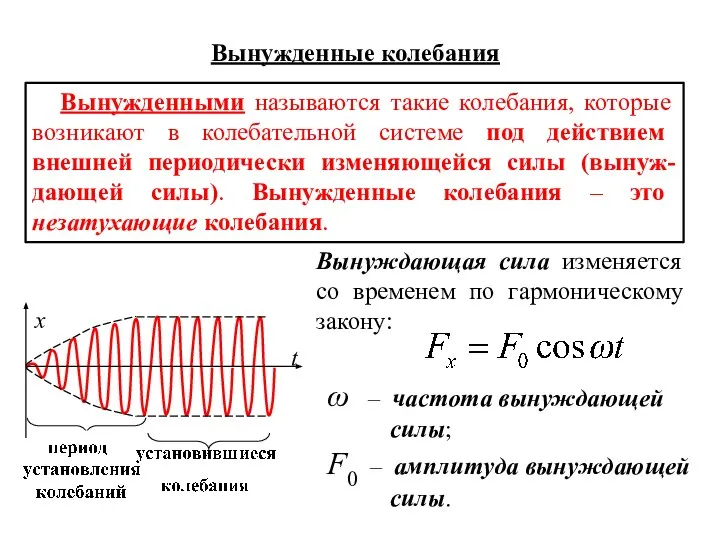
Вынужденные колебания
Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуж-дающей силы). Вынужденные колебания – это незатухающие колебания.
Вынуждающая сила изменяется со временем по гармоническому закону:
ω – частота вынуждающей
силы;
F0 – амплитуда вынуждающей
силы.

В уравнении движения (втором законе Ньютона) кроме квазиупругой силы и силы сопротивления среды учитываем вынуждающую силу:
Дифференциальное уравнение вынужденных колебаний:
Это неоднородное (правая часть отлична от нуля) дифференциальное уравнение второго порядка с постоянными коэффициентами.

Общее решение неоднородного уравнения равно сумме общего решения соответ-ствующего однородного уравнения, и частного решения данного неоднородного уравнения:
Первое слагаемое играет роль только при установлении колебаний. С течением времени из-за множителя e−βt роль этого слагаемого уменьшается. После установления колебаний первым слагаемым можно пренебречь, сохраняя лишь второе, которое описывает установившиеся вынужденные гармонические колебания с частотой, равной частоте вынуждающей силы:
Жан
Даламбер
(1717 – 1783)

Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы.
Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания ϕ также зависит от частоты вынуждающей силы.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к некоторому значению, называется резонансом, а соответствующая частота – резонансной частотой ωрез.
;

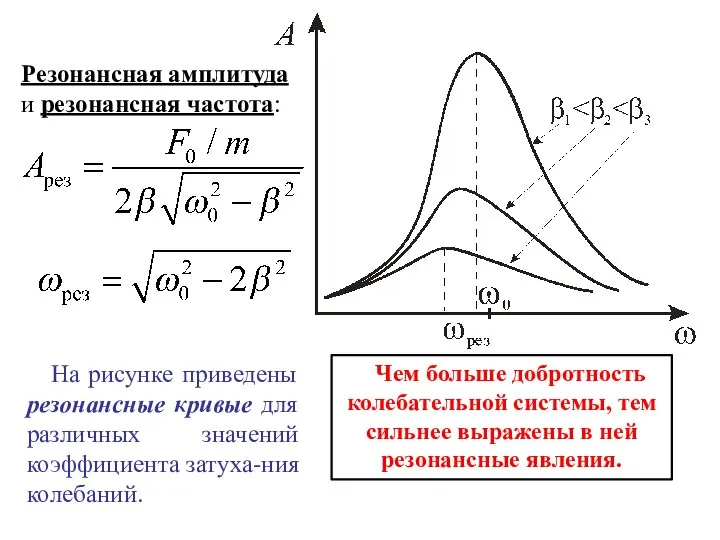
Резонансная амплитуда
и резонансная частота:
На рисунке приведены резонансные кривые для различных значений коэффициента затуха-ния колебаний.
Чем больше добротность колебательной системы, тем сильнее выражены в ней резонансные явления.