Молекулярная физика

Идеальный газ
Молекулы представлены как материальные точки
2. Между молекулами отсутствуют силы притяжения и отталкивания

Модель идеального газа была предложена в 1847 г. Дж. Герапатом
Эта модель является основой для МКТ
Модель идеального газа применяется для решения задач термодинамики газов и аэрогазодинамики
Все газы при н.у. Р = 1 атм. t = 0 °C ведут себя как идеальные

R = 8,31 Дж/моль⋅К – универсальная газовая постоянная
Уравнение состояния идеального газа
Уравнение Менделеева – Клапейрона:
k = 1,38⋅10-23 Дж/К – постоянная Больцмана

Три основных константы молекулярной физики
R = 8,31 Дж/моль⋅К – универсальная газовая постоянная
k = 1,38⋅10-23 Дж/К – постоянная Больцмана
NA = 6,02·1023 моль-1 – постоянная Авогадро

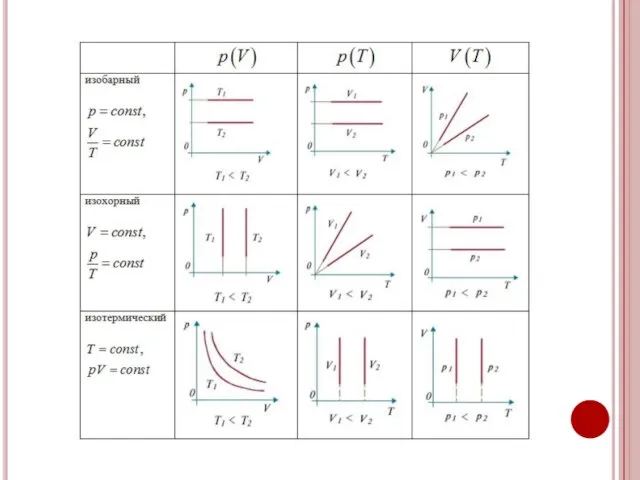
Изопроцессы в идеальных газах

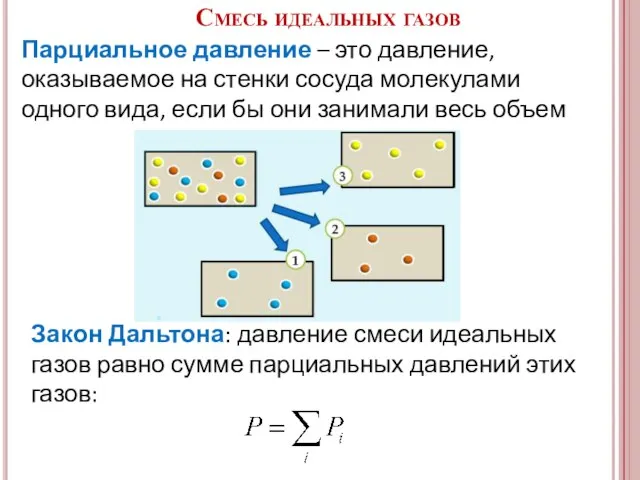
Парциальное давление – это давление, оказываемое на стенки сосуда молекулами одного вида, если бы они занимали весь объем
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений этих газов:
Смесь идеальных газов

– масса одной молекулы
– уравнение Клаузиуса – основное уравнение МКТ идеальных газов
Давление идеального газа на стенки сосуда
Давление газа на стенку сосуда определяется средним импульсом, передаваемым стенке молекулами газа при соударениях

T = t 0С + 273,15
1oС = 1 К
[К]
- средняя кинетическая энергия поступательного движения молекулы
Абсолютная температура - мера кинетической энергии поступательного движения молекул
Молекулярно-кинетический смысл температуры

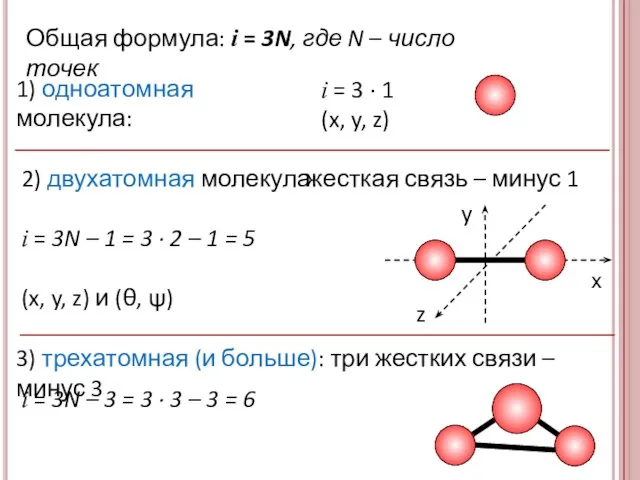
степени свободы молекулы
Степени свободы – число координат, определяющие положение тела в пространстве
Материальная точка i = 3 (x, y, z)
Твердое тело i = 6 (x, y, z) – задают центр масс
(θ, ψ, ϕ) – задают положение тела в пространстве
(x, y, z) – поступательные
(θ, ψ, ϕ) - вращательные

1) одноатомная молекула:
х
y
z
i = 3 · 1
(x, y, z)
i = 3N – 3 = 3 · 3 – 3 = 6
2) двухатомная молекула:
i = 3N – 1 = 3 · 2 – 1 = 5
(x, y, z) и (θ, ψ)
3) трехатомная (и больше): три жестких связи – минус 3
Общая формула: i = 3N, где N – число точек
жесткая связь – минус 1

- средняя кинетическая энергия молекулы
i - число степеней свободы
Средняя кинетическая энергия, приходящаяся при тепловом равновесии на одну любую степень свободы молекулы, равна ½·kT
Равномерное распределение кинетической энергии по степеням свободы молекулы