Содержание
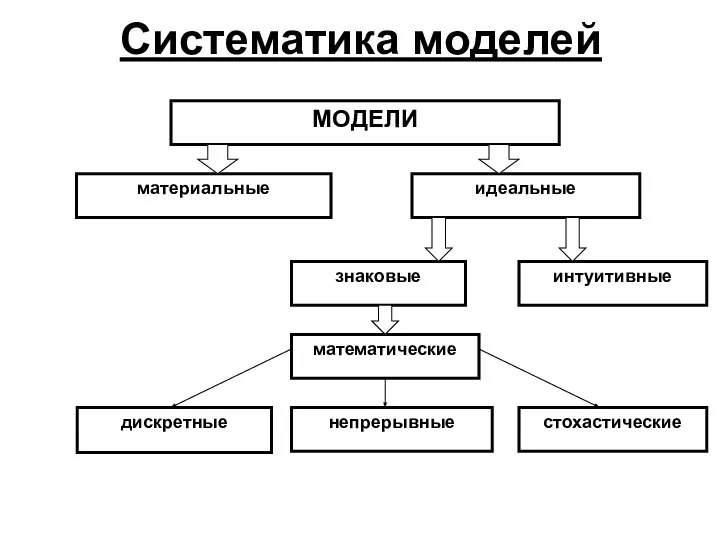
- 2. Систематика моделей МОДЕЛИ материальные идеальные знаковые интуитивные математические дискретные непрерывные стохастические
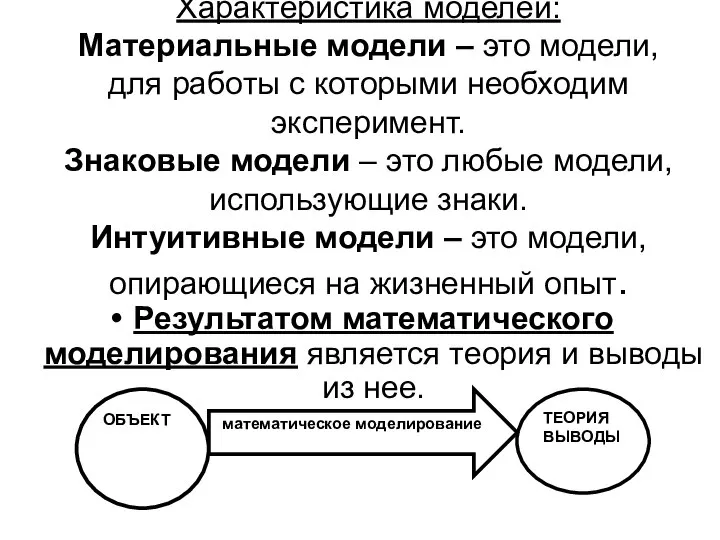
- 3. Характеристика моделей: Материальные модели – это модели, для работы с которыми необходим эксперимент. Знаковые модели –
- 4. Процесс моделирования: 1. Определение цели моделирования (что дано и что требуется найти). 2. Определение факторов, которые
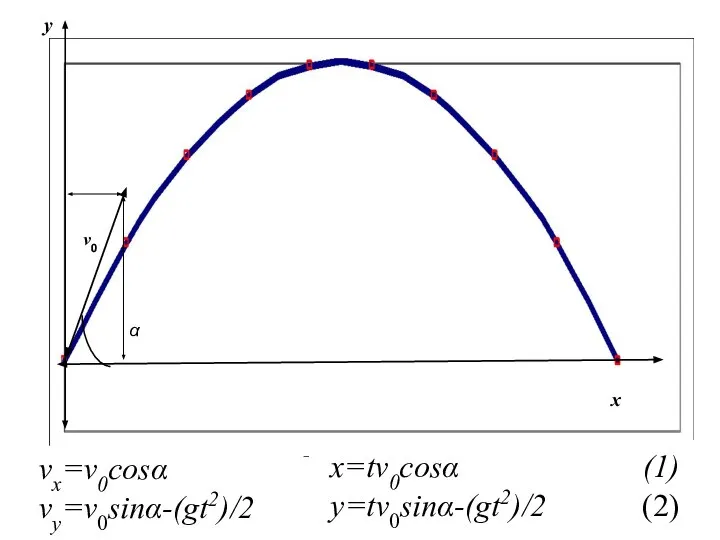
- 5. Задача баллистики. Задача: из катапульты бросают камень с начальной скоростью v0 под углом α к горизонту.
- 6. x y α v0 vx=v0cosα vy=v0sinα-(gt2)/2 x=tv0cosα (1) y=tv0sinα-(gt2)/2 (2)
- 7. Выражаем t из (1) и подставляем в (2). Получаем уравнение траектории: Чтобы определить дальность полета, нужно
- 8. Задача баллистики с учетом силы сопротивления воздуха. Из предположений модели исключаем предположение №4. Предположения модели: 1.
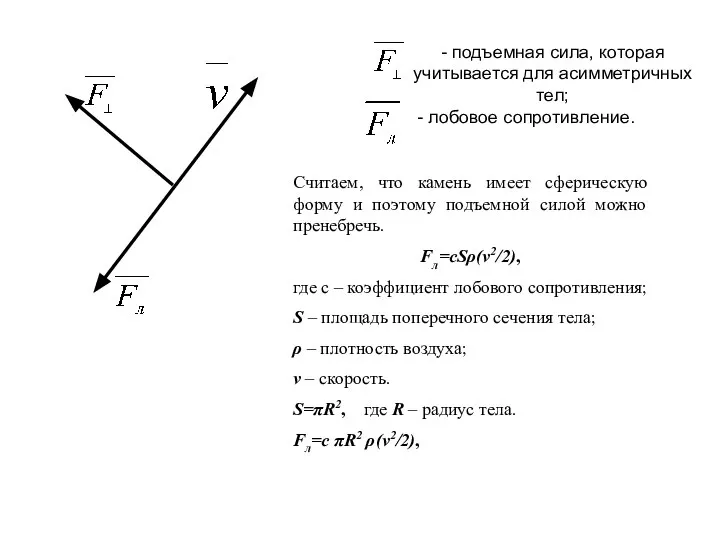
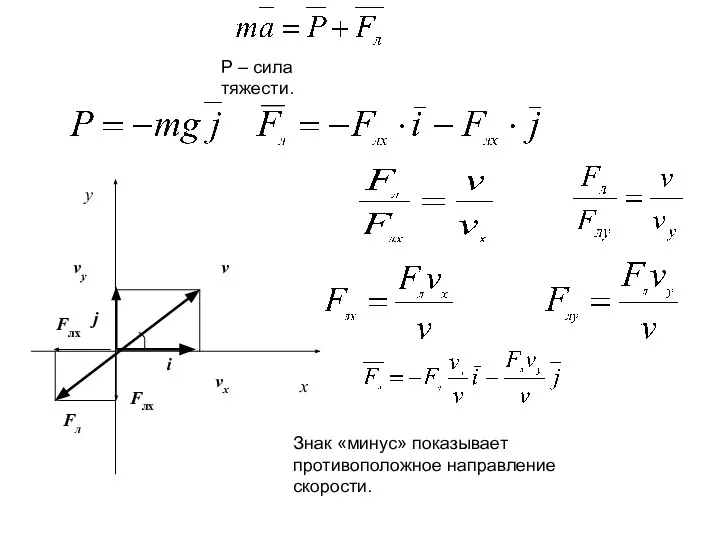
- 9. - подъемная сила, которая учитывается для асимметричных тел; - лобовое сопротивление. Считаем, что камень имеет сферическую
- 10. Знак «минус» показывает противоположное направление скорости. i j x y v Fл Fлx Fлx vy vx
- 11. Подставляем Fл в уравнение (*): Разделим обе части уравнения на m: Перейдем от этого уравнения к
- 12. x(t)≡x y(t)≡y vx=x’ vy=y’ ax=x’’ ay=y’’ Чтобы решить эту систему, нужно знать начальные условия. Начальные условия:
- 13. Начальные условия: U1(0)=0; U2(0)=v0cosα; U3(0)=0; U4(0)=v0sinα. Решением этой системы будут функции при заданных начальных условиях.
- 15. ТЕМА: КРАЕВАЯ ЗАДАЧА Постановка задачи. Снаряд летит с постоянной скоростью под углом α к горизонту. Цель
- 16. Система дифференциальных уравнений: Граничные условия (начальные условия, которые задаются на концах отрезка):
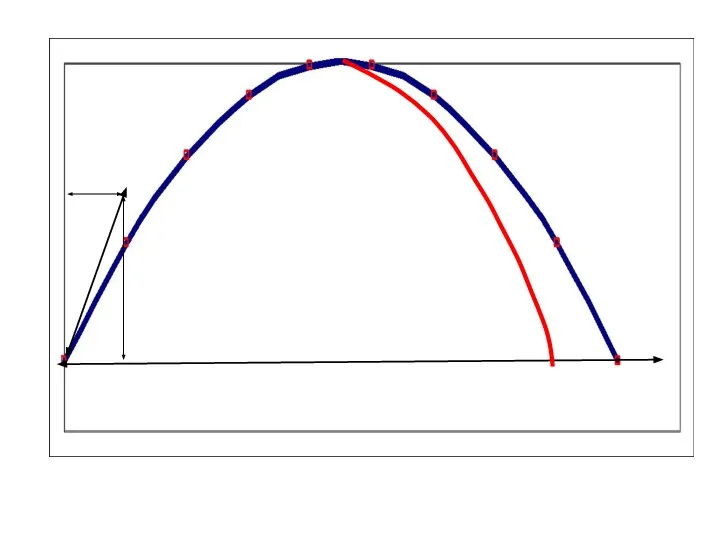
- 17. Дальность полета максимальна при α=45º. Мы можем решить задачу Коши при α =45º. Получим некоторую траекторию,
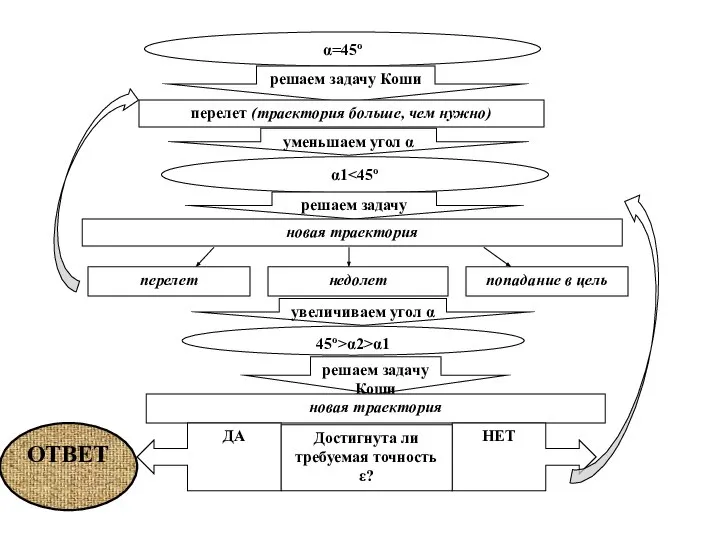
- 18. α=45º решаем задачу Коши перелет (траектория больше, чем нужно) уменьшаем угол α α1 решаем задачу Коши
- 19. где: где — вектор начальных условий, а — вектор правых частей. — вектор, содержащий решение, Задача
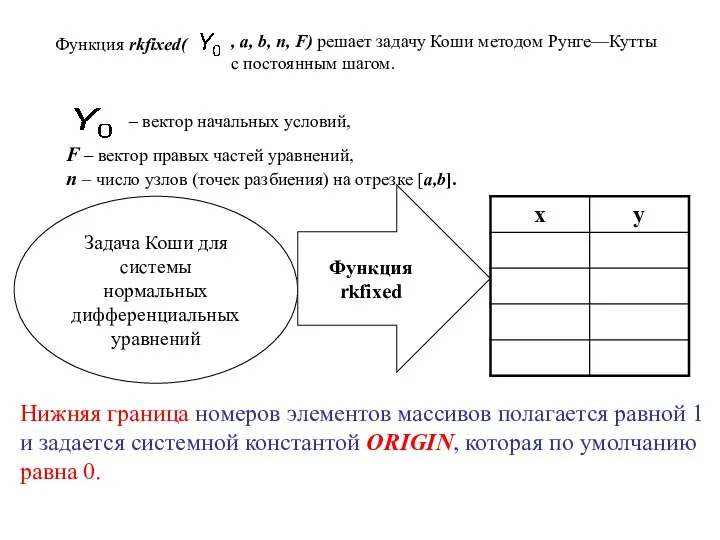
- 20. Задача Коши для системы нормальных дифференциальных уравнений РЕШЕНИЕ ЗАДАЧИ ? КАК ЭТО СДЕЛАТЬ В MATHCAD? Функция
- 21. Функция rkfixed( , a, b, n, F) решает задачу Коши методом Рунге—Кутты с постоянным шагом. –
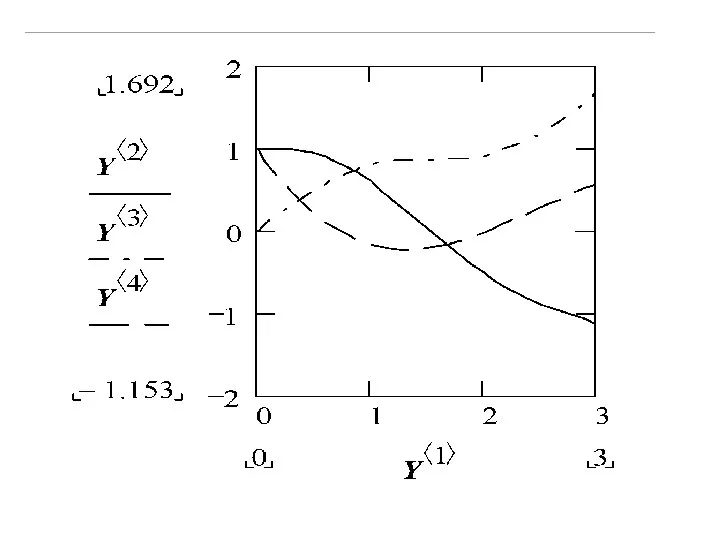
- 22. Пример. Решить систему дифференциальных уравнений на отрезке [0,3] с шагом 0.1, построить графики найденных функций. Решение
- 24. В этой модели учитывается один показатель: количество публикаций в данный момент. х(t)≡х; ПРЕДПОЛОЖЕНИЕ: скорость роста количества
- 25. Запишем дифференциальное уравнение: Решением уравнения такого вида является функция вида еt; et→∞; t→∞. ! Такую модель
- 26. Модель численности популяций. N(t) – численность популяции в момент времени t. Скорость v роста популяции прямо
- 27. Пример 3. Модель гонки вооружений Ричардсона. x(t)≡x – расходы на вооружение «зеленых»; y(t)≡y – расходы на
- 28. ПРЕДПОЛОЖЕНИЕ 3: Предположим, что у каждого государства могут быть какие-то претензии. Введем коэффициенты претензий r и
- 29. КОГДА ДОСТИГАЕТСЯ РАВНОВЕСИЕ? Точка равновесия достигается при следующем условии: x=(a/m)y+(r/m); x=(n/b)y-s/b; (a/m)y+r/m= (n/b)y-s/b; y(a/m-n/b)=-s/b-r/m.
- 30. Точка, в которой достигается равновесие, имеет следующие координаты: Каждая точка этой координатной плоскости характеризуется: 1. Координатами
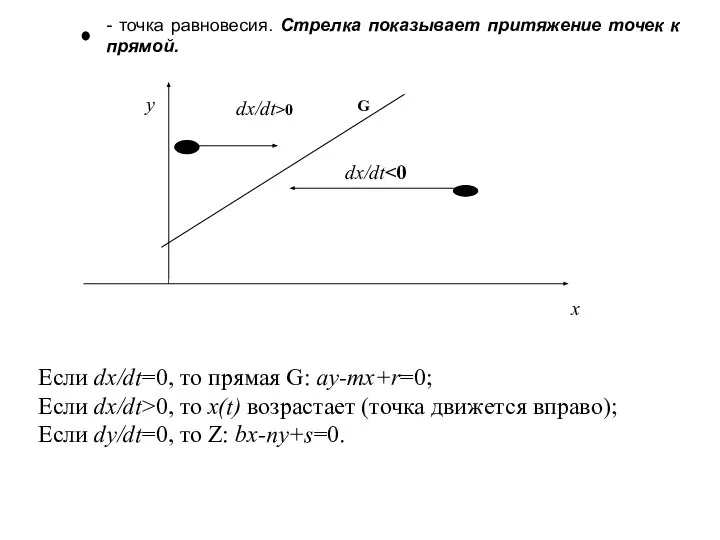
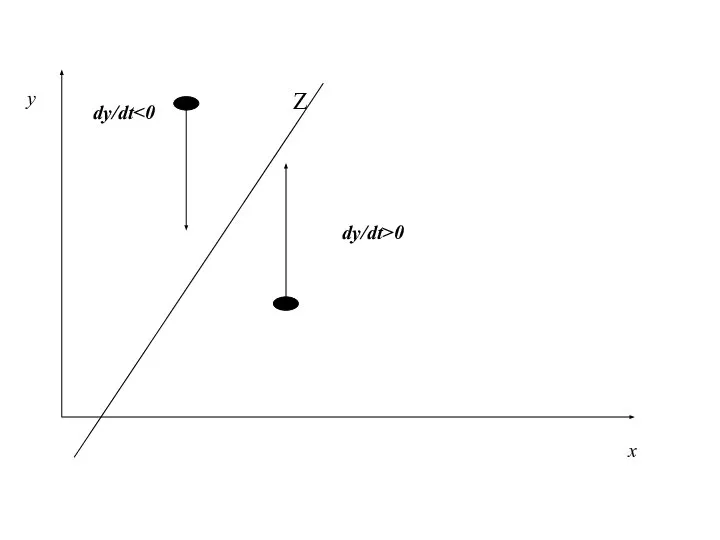
- 31. - точка равновесия. Стрелка показывает притяжение точек к прямой. Если dx/dt=0, то прямая G: ay-mx+r=0; Если
- 32. х y
- 33. Исследуем поведение системы в зависимости от начальных условий. В зависимости от коэффициентов m, n, r, s
- 34. Вариант 2. mn-ab>0; r, s x(t), y(t)≥0. Точка равновесия не достижима ни при каких начальных условиях.
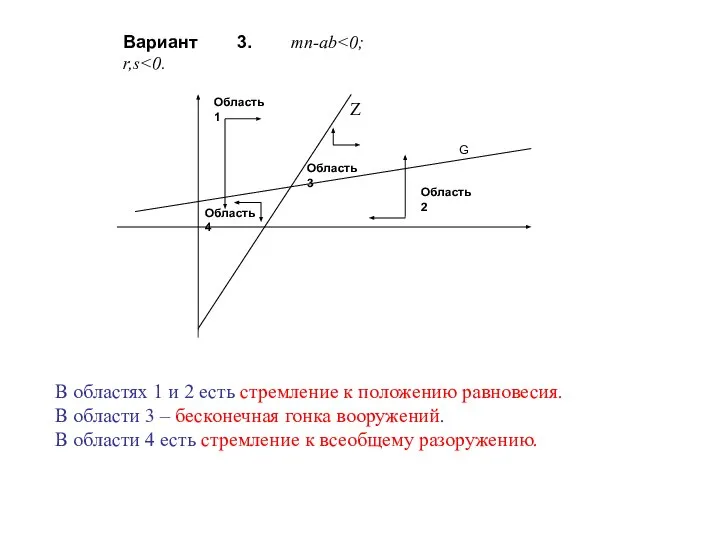
- 35. Вариант 3. mn-ab В областях 1 и 2 есть стремление к положению равновесия. В области 3
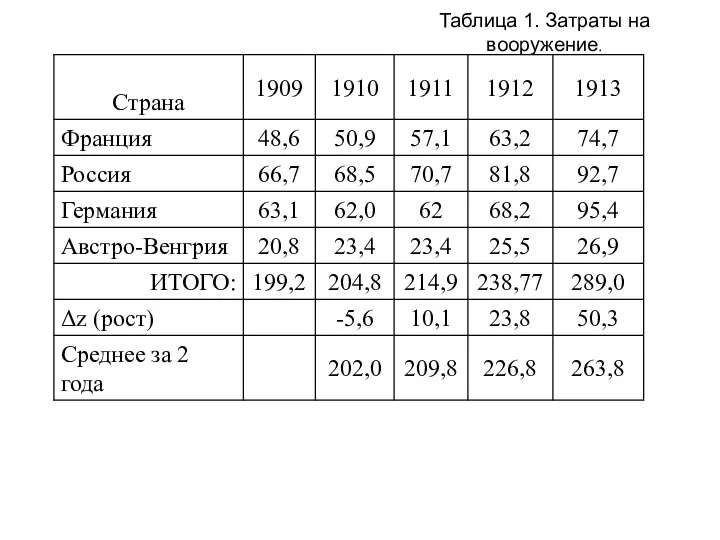
- 36. ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ делалась на реальных данных. Рассматривались 2 блока: х – Россия и Франция; у
- 37. Таблица 1. Затраты на вооружение.
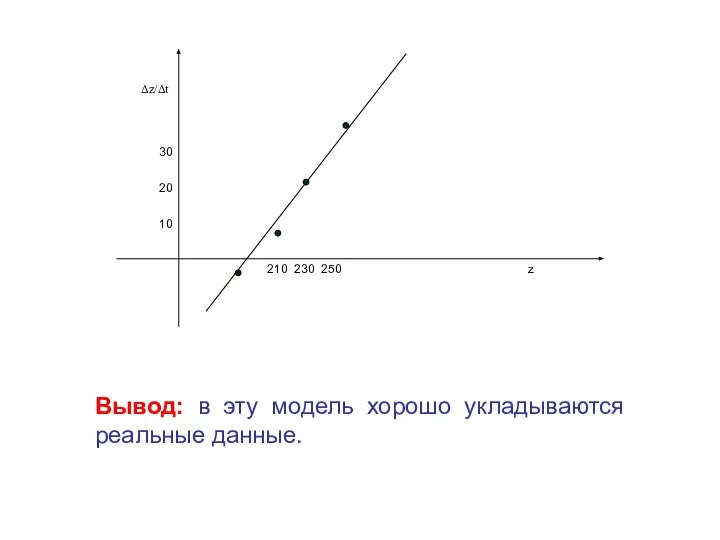
- 38. Δz/Δt z 10 230 250 210 20 30 Вывод: в эту модель хорошо укладываются реальные данные.
- 39. Моделирование прогиба балки
- 40. На свободный конец балки единичной длины и постоянной жесткости (ЕJ=1, Е – модуль Юнга , J
- 41. Прогиб балки описывается нелинейным дифференциальным уравнением : с граничными условиями: . с граничными условиями: .
- 42. Если известно φ(S), то декартовы координаты точек изогнутой оси балки можно определить из следующих соображений: малому
- 43. Решение задачи КОШИ для обыкновенного дифференциального уравнения odesolve(x,b,step), Обращение к функции имеет вид y:=odesolve(x,b) или y:=odesolve(x,b,step),
- 44. Решение в Mathcad
- 45. Применение метода конечных разностей дифференциальная задача сводится к решению системы алгебраических уравнений. Длина балки разбивается на
- 46. При для аппроксимации производной требуется значение угла φn+1 в несуществующем узле с номером n+1. Оно определяется
- 47. При малых прогибах балки можно считать и решать систему линейных уравнений относительно .
- 48. Решение уравнений в частных производных Уравнения в частных производных используются при моделировании разнообразных физических процессов: задачи
- 49. Общий вид дифференциального уравнения 2–го порядка с двумя независимыми переменными: где u≡u(x,y), неизвестная функция, х и
- 50. ТИПЫ уравнений в частных производных Тип уравнения определяется по виду коэффициентов и соотношениям между ними. Обычно
- 51. Рассмотрим дифференциальное уравнение в частных производных первого порядка: , u(t,x) – неизвестная функция двух независимых переменных
- 52. Уравнение Пуассона Это уравнение эллиптического типа, которое можно решить в Mathcad с помощью встроенной функции Уравнение
- 53. Функция multigrid (f, r) имеет два аргумента: f – имя матрицы, задающей правую часть уравнения; r
- 54. Пример 2. Решить уравнение Пуассона, если при , m = 32 , имеются два источника тепла
- 55. Аппроксимация частных производных функция двух переменных. Пусть область решения заменена сеткой, узлы сетки имеют координаты (i,j)
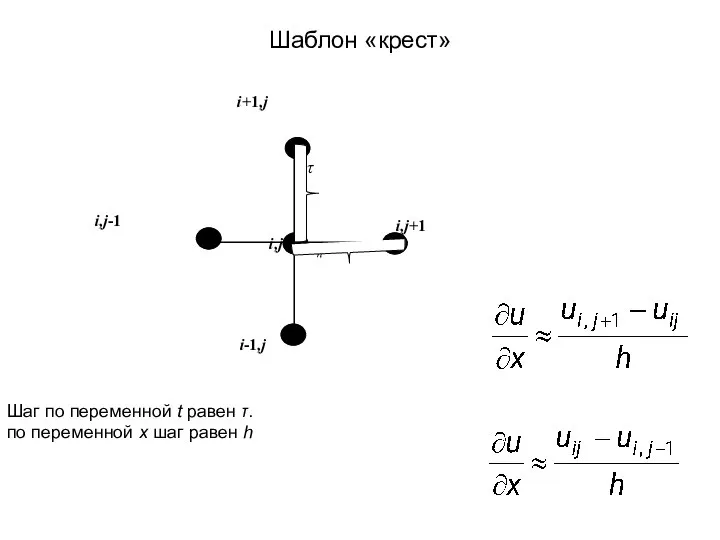
- 56. Шаблон «крест» Шаг по переменной t равен τ. по переменной x шаг равен h
- 57. По этому шаблону частные производные функции в узле (i,j) можно аппроксимировать следующим образом: ; ; ;
- 58. Дифференциальное уравнение в частных производных первого порядка: ,u(t,x) – неизвестная функция двух независимых переменных t, x;
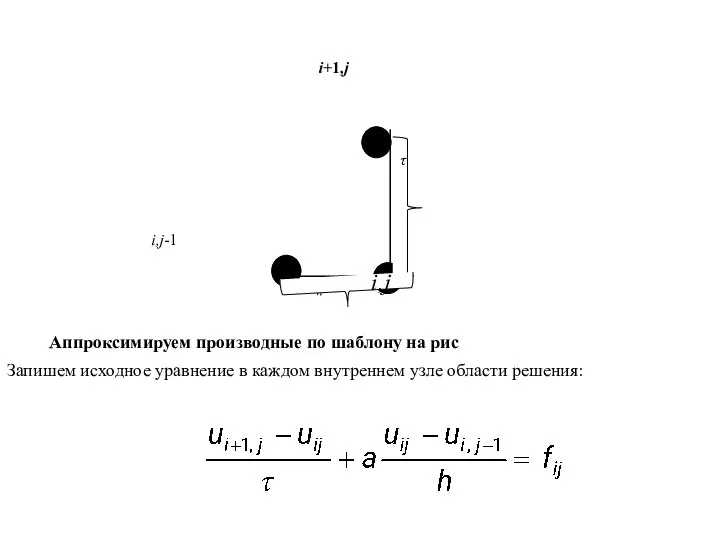
- 59. Аппроксимируем производные по шаблону на рис Запишем исходное уравнение в каждом внутреннем узле области решения:
- 60. Отсюда где i=0,1,2,…,n; j=0,1,2,…, m Вычисления идут по слоям. На нулевом слое u0j=φj (φi вычисляется как
- 61. Схема устойчива при 0≤τ≤h/a, при этом u(t,x), φ(х), ψ(t) должны быть дважды непрерывно дифференцируемы; f(х,t) имеет
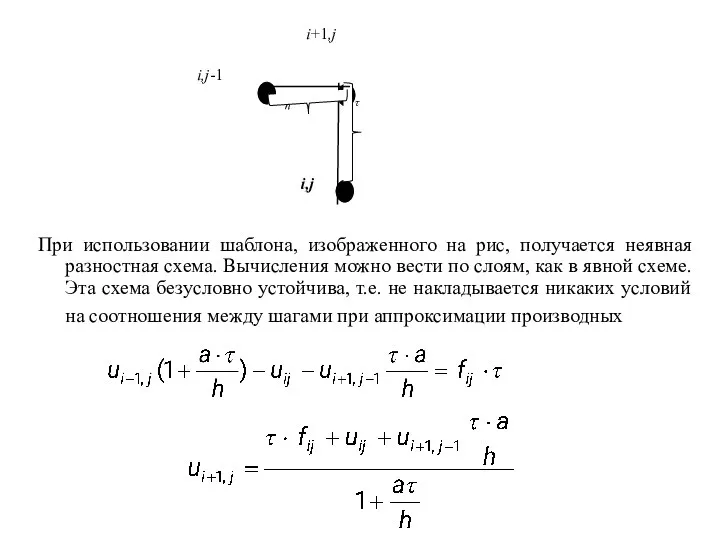
- 62. При использовании шаблона, изображенного на рис, получается неявная разностная схема. Вычисления можно вести по слоям, как
- 63. Пример.
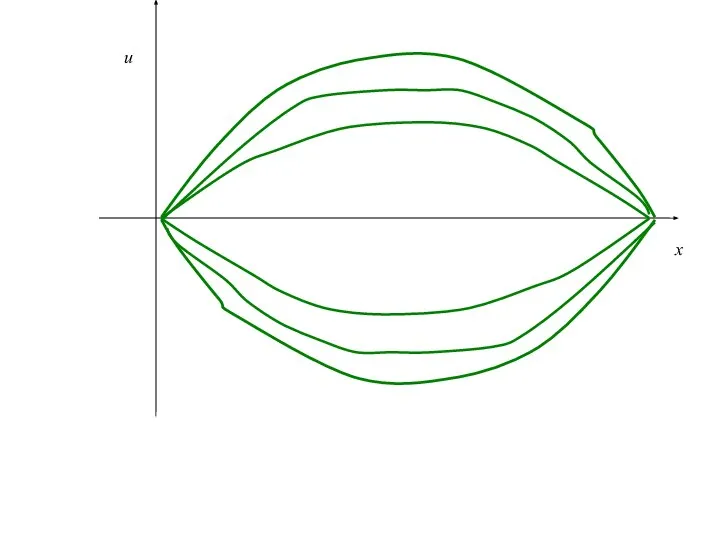
- 64. Уравнение колебания струны Рассмотрим одномерное волновое уравнение, которое описывает, например, свободное колебание струны из исходного неравновесного
- 65. x u
- 67. Скачать презентацию












![Пример. Решить систему дифференциальных уравнений на отрезке [0,3] с шагом 0.1, построить](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1023758/slide-21.jpg)














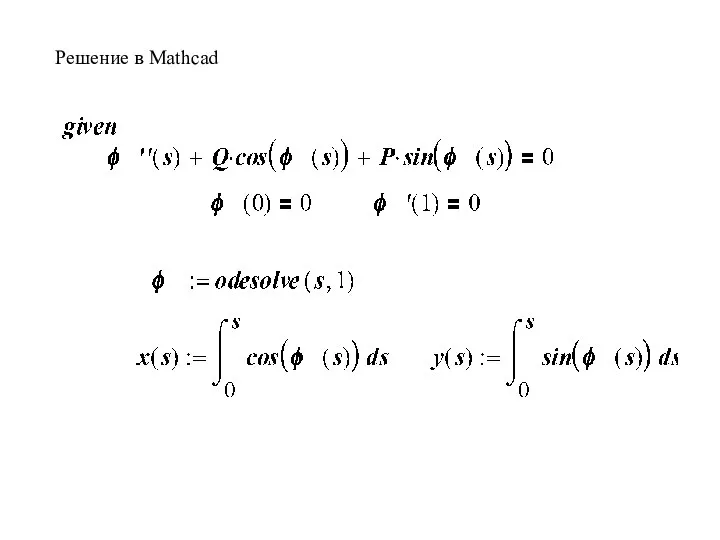















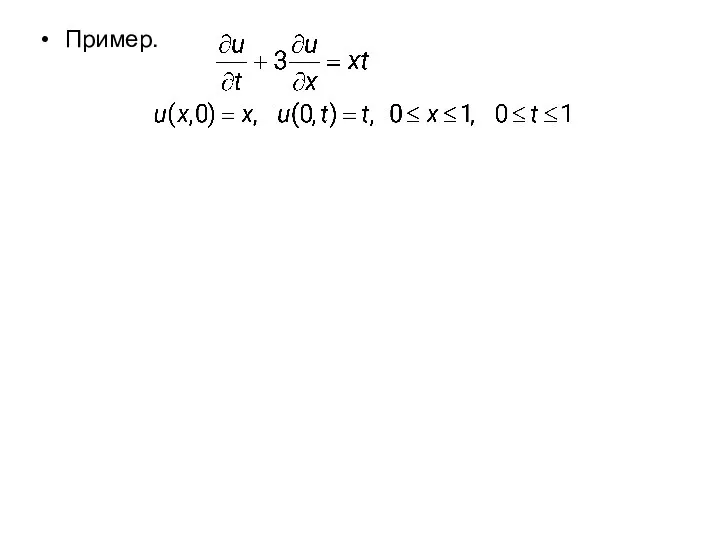

 Расчет направляющих. Анализ напряжений и деформаций направляющих в процессе работы ловителя
Расчет направляющих. Анализ напряжений и деформаций направляющих в процессе работы ловителя Занимательные опыты по физике
Занимательные опыты по физике Линзы. Оптика
Линзы. Оптика Заряды. Закон Кулона
Заряды. Закон Кулона Свердління отворів. Оброблення країв виробів
Свердління отворів. Оброблення країв виробів Il modello atomico di Schrödinger
Il modello atomico di Schrödinger Типовые соединения деталей машин
Типовые соединения деталей машин Вынужденные электромагнитные колебания
Вынужденные электромагнитные колебания Манометры
Манометры Решение задач репетиционного тестирования по физике, этап 1
Решение задач репетиционного тестирования по физике, этап 1 Основы аэродинамики
Основы аэродинамики sokhranenie_impulsa
sokhranenie_impulsa Лабораторные работы по курсу Математическое моделирование технических систем
Лабораторные работы по курсу Математическое моделирование технических систем Действие магнитного поля на проводник с током. Сила Ампера
Действие магнитного поля на проводник с током. Сила Ампера Курчатов Игорь Васильевич
Курчатов Игорь Васильевич Умная колонка на уроках физики
Умная колонка на уроках физики Обобщающий урок-соревнование по теме Электрические явления
Обобщающий урок-соревнование по теме Электрические явления Экспериментальные методы в радиофизике
Экспериментальные методы в радиофизике Электроэнергия. Гидроэлектростанция. Линия электропередач. Электролампа
Электроэнергия. Гидроэлектростанция. Линия электропередач. Электролампа Ядерные силы. Ядерные реакции
Ядерные силы. Ядерные реакции Классная физика. Квест-игра
Классная физика. Квест-игра Энергия системы неподвижных точечных зарядов
Энергия системы неподвижных точечных зарядов Презентация на тему Конвекция. Излучение
Презентация на тему Конвекция. Излучение  Популярные типы кузова автомобилей
Популярные типы кузова автомобилей Источники света. Распространение света
Источники света. Распространение света Цилиндрические зубчатые передачи. Лекции 8
Цилиндрические зубчатые передачи. Лекции 8 Разработкой технологии дефектации прибора системы зажигания автомобиля ГАЗ-2752 Газель
Разработкой технологии дефектации прибора системы зажигания автомобиля ГАЗ-2752 Газель Магнитное поле. Действие магнитного поля на проводник с током
Магнитное поле. Действие магнитного поля на проводник с током