Общий порядок построения эпюр Qx и Мх

При наличии распределенной нагрузки необходимо найти экстремальное значение Мх на этом участке, для чего надо знать, на каком расстоянии от точки начала действия распределенной нагрузки находится сечение с экстремальным значением Мх. Определяют это расстояние 2-мя способами:
- находят первую производную от выражения момента и приравнивают ее нулю: dМх/dх=0;
- определяют по эпюре Qх, рассматривая подобие треугольников.
Пример 5.1 Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной на рисунке 5.1,а, если F=10кН и l=4м.
Решение:
1. Определяем опорные реакции. Поскольку балка имеет ось симметрии относительно опор, то очевидно, что опорные реакции:
RA=RВ=F/2=5кН
2. Разбиваем балку на два участка ( и  )
3. Определяем поперечные силы Qх на каждом участке.

Участок  (0≤ х1 ≤ l/2)
Qх1 = RA = F/2 = 5кН
Участок  (l/2≤ х2 ≤ l)
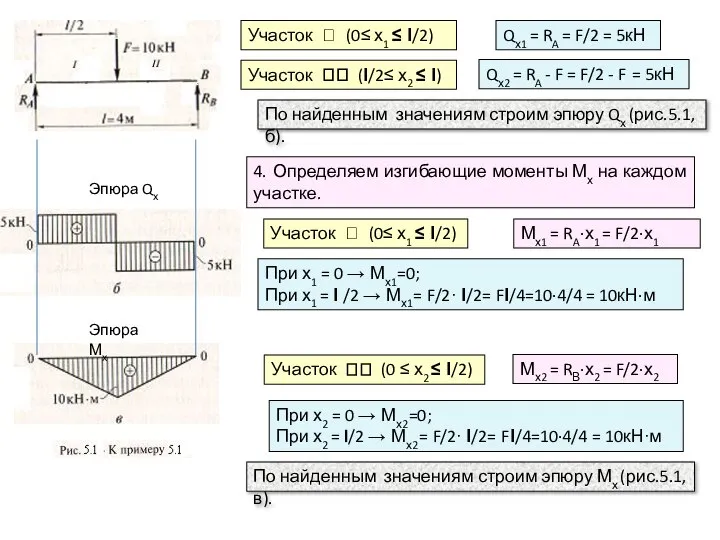
Qх2 = RA - F = F/2 - F = 5кН
По найденным значениям строим эпюру Qх (рис.5.1,б).
Эпюра Qх
4. Определяем изгибающие моменты Мх на каждом участке.
Участок  (0≤ х1 ≤ l/2)
Мх1 = RA∙х1 = F/2∙х1
Эпюра Мх
При х1 = 0 → Мх1=0;
При х1 = l /2 → Мх1= F/2∙ l/2= Fl/4=10∙4/4 = 10кН∙м
По найденным значениям строим эпюру Мх (рис.5.1,в).
Участок  (0 ≤ х2 ≤ l/2)
Мх2 = RВ∙х2 = F/2∙х2
При х2 = 0 → Мх2=0;
При х2 = l/2 → Мх2= F/2∙ l/2= Fl/4=10∙4/4 = 10кН∙м

Пример 5.2 Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной на рисунке 5.2,а, если F=5кН, l=4м, а=1м
Решение:
1. Определяем опорные реакции:
Проверка:
0≡0. Опорные реакции найдены правильно
2. Разбиваем балку на три участка ( - ). Для 3-го участка лучше рассматривать правую часть балки.
3. Определяем поперечные силы Qх на каждом участке.
Участок  (0≤ х1 ≤ а)
Qх1 = -F= -5кН-на всем участке
Участок  (а≤ х2 ≤ а + l/2)
Qх2 = - F+RA= -5+11,25 = 6,25кН

Участок  (0≤ х2 ≤ l/2)
Qх3 = - RВ= - 3,75кН
По найденным значениям строим эпюру Qх (рис.5.2,б).
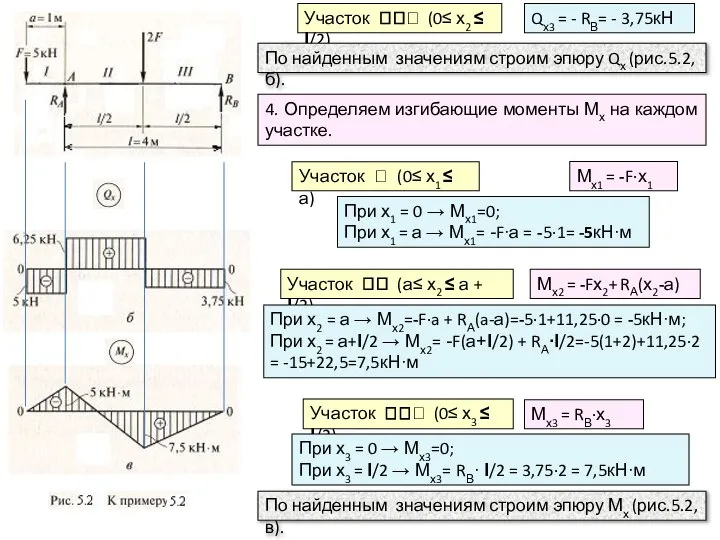
4. Определяем изгибающие моменты Мх на каждом участке.
Участок  (0≤ х1 ≤ а)
Участок  (а≤ х2 ≤ а + l/2)
Участок  (0≤ х3 ≤ l/2)
Мх1 = -F∙х1
При х1 = 0 → Мх1=0;
При х1 = а → Мх1= -F∙а = -5∙1= -5кН∙м
При х2 = а → Мх2=-F∙a + RА(a-а)=-5∙1+11,25∙0 = -5кН∙м;
При х2 = а+l/2 → Мх2= -F(а+l/2) + RА∙l/2=-5(1+2)+11,25∙2 = -15+22,5=7,5кН∙м
Мх2 = -Fх2+ RА(х2-а)
Мх3 = RВ∙х3
При х3 = 0 → Мх3=0;
При х3 = l/2 → Мх3= RВ∙ l/2 = 3,75∙2 = 7,5кН∙м
По найденным значениям строим эпюру Мх (рис.5.2,в).

Пример 5.3 Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной на рисунке 5.3,а, если q=10кН/м, l=3,5м.
Решение:
1. Определяем опорные реакции:
При определении опорных реакций удобнее заменить распределенную нагрузку сосредоточенной, величина которой равна произведению интенсивности нагрузки на длину участка ее приложения (l/2). Составляем уравнения равновесия (рис.5.3,а):
Проверка:
0≡0. Опорные реакции найдены правильно

2. Разбиваем балку на три участка ( - ).
3. Определяем поперечные силы Qх на каждом участке.
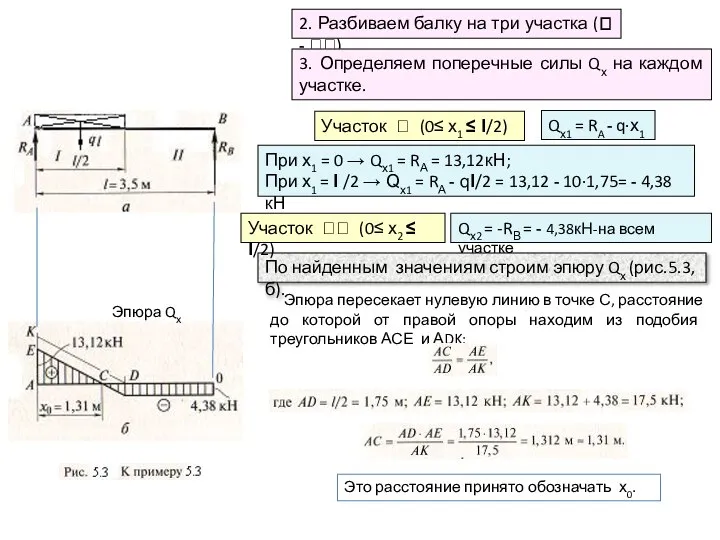
Участок  (0≤ х1 ≤ l/2)
Qх1 = RA - q∙х1
Qх2 = -RВ = - 4,38кН-на всем участке
По найденным значениям строим эпюру Qх (рис.5.3,б).
При х1 = 0 → Qх1 = RА = 13,12кН;
При х1 = l /2 → Qх1 = RА - ql/2 = 13,12 - 10∙1,75= - 4,38кН
Участок  (0≤ х2 ≤ l/2)
Эпюра Qх
Эпюра пересекает нулевую линию в точке С, расстояние до которой от правой опоры находим из подобия треугольников АСЕ и АDK:
Это расстояние принято обозначать х0.

4. Определяем изгибающие моменты Мх на каждом участке.
Участок  (0≤ х1 ≤ l/2)
Мх1 = RA∙х1 - q∙х12
Участок  (0≤ х2 ≤ l/2)
Мх2 = RВ∙х2
При х1 = 0 → Мх1 = 0;
При х1 = l /2 → Мх1 = RA∙l/2 – q∙(l/2)2 /2 = 13,12∙1,75-10∙1,752/2 = 22,96 - 15,31 = 7,65кН∙м
При х1 =х0 =1,31м → Мх1 = RA∙х0 - q∙х02/2 = 13,12∙1,31-10∙1,312/2 = 17,19 - 8,58 = 8,61кН∙м;
При х2 = 0 → Мх2 = 0;
При х2 = l /2 → Мх2= RВ∙l/2 = 4,38 ∙ 1,75 = 7,66кН∙м
Суммы моментов всех сил слева и справа получились примерно одинаковыми – 7,65 и 7,66кН∙м. Незначительное расхождение произошло из-за округления значений опорных реакций. Соединяем плавной кривой отложенные значения и получаем на участке AD параболу выпуклостью вниз (рис.5.3,в).
Эпюра Мх
По найденным значениям строим эпюру Мх (рис.5.3,в).

Проанализировав эпюры Qх и Мх с позиции их изменения по длине балки, можно сделать выводы

Для самостоятельного решения !
Задача 3. Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной на рис. 5.4 при заданных М и l . Исходные данные взять из таблицы 1 по последней цифре зачетной книжки.
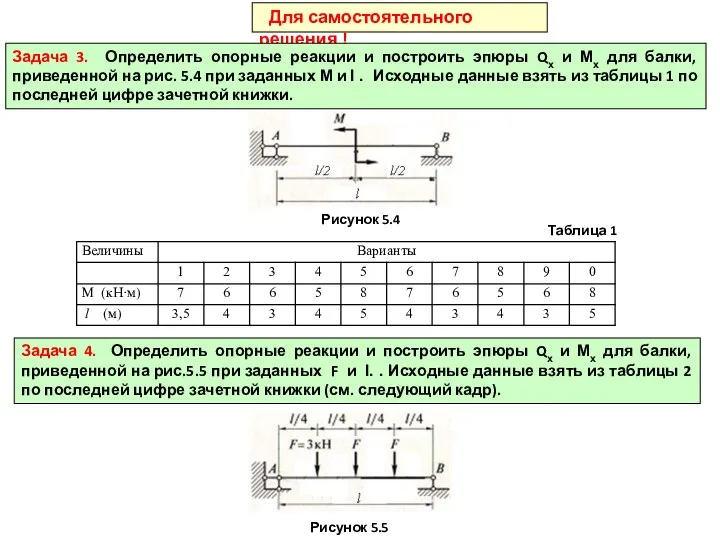
Рисунок 5.4
Рисунок 5.5
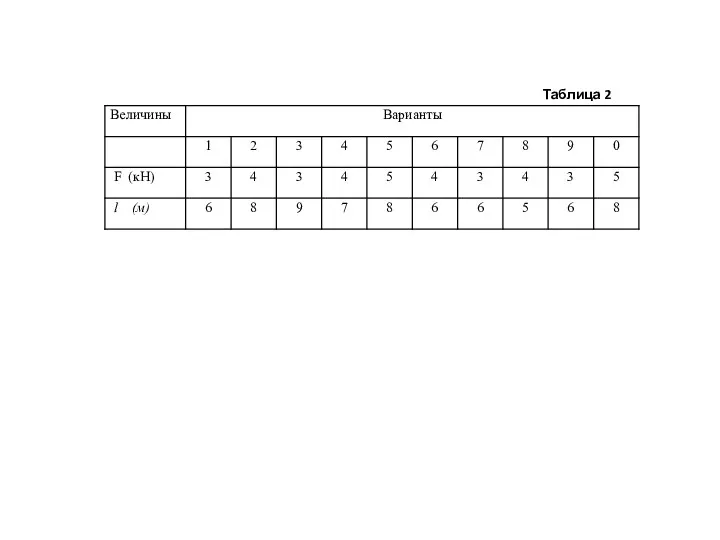
Задача 4. Определить опорные реакции и построить эпюры Qх и Мх для балки, приведенной на рис.5.5 при заданных F и l. . Исходные данные взять из таблицы 2 по последней цифре зачетной книжки (см. следующий кадр).
Таблица 1

Таблица 2

5.2 Построение эпюр способом «по характерным точкам»
1. Определяют опорные реакции.
2. Обозначают характерные точки.
3. Определяют значения Qх и Мх в характерных точках.
4. Точки, соответствующие полученным значениям, соединяют между собой. При этом необходимо учитывать следующее. В местах приложения сосредоточенных сил надо отыскивать два значения поперечной силы Qх (Qлев и Qправ ), которые отличаются друг от друга на величину сосредоточенной силы. Аналогично при построении эпюры изгибающих моментов в точке, где приложен внешний сосредоточенный момент, необходимо находить два значения Мх (Млев и Мправ ), которые отличаются друг от друга на величину внешнего момента.
5. Оба значения Qх (Qлев и Qправ ) и Мх (Млев и Мправ ) могут быть найдены при рассмотрении левой части балки, либо одно из значений находят, рассматривая левую часть балки, а второе – правую.