Содержание
- 2. Принято внешние силовые факторы называть вращающими или скручивающими моментами и обозначать М; внутренние усилия – крутящим
- 3. 6.2. Построение эпюр крутящих моментов Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих
- 4. Эпюра крутящих моментов – график изменения крутящих моментов по длине бруса. Во всех случаях эпюры внутренних
- 7. Скачать презентацию
Слайд 2 Принято внешние силовые факторы называть вращающими или скручивающими моментами и обозначать
Принято внешние силовые факторы называть вращающими или скручивающими моментами и обозначать

М; внутренние усилия – крутящим моментом Мk.
Крутящий момент - это внутренний момент, возникающий в сечении вала, равный сумме скручивающих (внешних) моментов, расположенных по одну сторону от сечения.
Прежде чем приступить к определению напряжений обратимся к рассмотрению результатов опытов на кручение вала круглого сечения. Впервые эти опыты были проведены Кулоном. Им были введены следующие гипотезы (допущения):
1. ось вала после деформации остается прямой;
2. все поперечные сечения вала остаются плоскими и после деформации;
3. радиусы поперечных сечений при деформации остаются прямыми;
4. расстояния между сечениями не изменяются;
5. все образующие вала поворачиваются на один и тот же угол;
6. каждое поперечное сечение поворачивается относительно друг друга на
некоторый угол, называемый углом закручивания.
Крутящий момент - это внутренний момент, возникающий в сечении вала, равный сумме скручивающих (внешних) моментов, расположенных по одну сторону от сечения.
Прежде чем приступить к определению напряжений обратимся к рассмотрению результатов опытов на кручение вала круглого сечения. Впервые эти опыты были проведены Кулоном. Им были введены следующие гипотезы (допущения):
1. ось вала после деформации остается прямой;
2. все поперечные сечения вала остаются плоскими и после деформации;
3. радиусы поперечных сечений при деформации остаются прямыми;
4. расстояния между сечениями не изменяются;
5. все образующие вала поворачиваются на один и тот же угол;
6. каждое поперечное сечение поворачивается относительно друг друга на
некоторый угол, называемый углом закручивания.
Слайд 36.2. Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо
6.2. Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо

знать значения внутренних крутящих моментов Mk в поперечных сечениях по длине вала.
Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В расчетах на прочность и жесткость при кручении знак крутящего момента значения не имеет, но для удобства построения эпюр принято правило:
Крутящий момент считают положительным, если при взгляде в торец отсеченной части бруса он стремится вращать сечение против хода часовой стрелки.
На основании метода сечений крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних
скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В расчетах на прочность и жесткость при кручении знак крутящего момента значения не имеет, но для удобства построения эпюр принято правило:
Крутящий момент считают положительным, если при взгляде в торец отсеченной части бруса он стремится вращать сечение против хода часовой стрелки.
На основании метода сечений крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних
скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
Слайд 4Эпюра крутящих моментов – график изменения крутящих моментов по длине бруса.
Во всех
Эпюра крутящих моментов – график изменения крутящих моментов по длине бруса.
Во всех

случаях эпюры внутренних усилий строят на осевой линии бруса. Величину силового фактора откладывают по нормали к оси.
M1= 180 Н∙м
M2= 150 Н∙м
M3= 450 Н∙м
M4= 120 Н∙м
- Предыдущая
a404a48b8f70a1fc0dcf692Следующая -
Условия для образования органа зрения
 Фундаментальные физические величины. Упражнения. Часть 2
Фундаментальные физические величины. Упражнения. Часть 2 Презентация урока физики в 8 классе «Параллельное соединение проводников ». Автор: Глазунова Лидия Ивановна, учитель физики МБО
Презентация урока физики в 8 классе «Параллельное соединение проводников ». Автор: Глазунова Лидия Ивановна, учитель физики МБО Электростатика. Сила Кулона
Электростатика. Сила Кулона Виды излучений. Источники света
Виды излучений. Источники света Основное оборудовние тепловых насосов
Основное оборудовние тепловых насосов Электрические машины. Вращающееся магнитное поле. Трехфазные асинхронные двигатели
Электрические машины. Вращающееся магнитное поле. Трехфазные асинхронные двигатели Сверхпроводимость. ВТСП структуры
Сверхпроводимость. ВТСП структуры Урок-конференция
Урок-конференция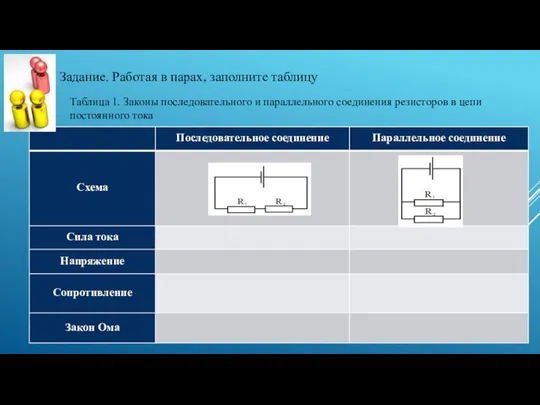 Закон Ома для последовательной электрической цепи переменного тока, содержащей активное и реактивное сопротивления
Закон Ома для последовательной электрической цепи переменного тока, содержащей активное и реактивное сопротивления Магнитное поле. Лекция 19. Закон Био-Савара-Лапласа. Теорема о циркуляции вектора магнитной индукции
Магнитное поле. Лекция 19. Закон Био-Савара-Лапласа. Теорема о циркуляции вектора магнитной индукции Ядерный реактор
Ядерный реактор Интегральные параметры переменного напряжения
Интегральные параметры переменного напряжения Двигуни внутрішнього згоряння
Двигуни внутрішнього згоряння Физика в картинках. Пирамиды в Гизе
Физика в картинках. Пирамиды в Гизе Что изучает физика
Что изучает физика Презентация на тему Электрические явления
Презентация на тему Электрические явления  Обратные задачи определения источника в уравнении теплопроводности
Обратные задачи определения источника в уравнении теплопроводности Ультразвук
Ультразвук Световое давление Урок для 11 класса.
Световое давление Урок для 11 класса. Изгиб. Основные понятия. Классификация видов изгибов
Изгиб. Основные понятия. Классификация видов изгибов Необходимость создания приемной антенно цифровой решетки для ультразвуковой безэховой камеры
Необходимость создания приемной антенно цифровой решетки для ультразвуковой безэховой камеры Параллельная работа одинаковых трубопроводов
Параллельная работа одинаковых трубопроводов قانون گاوس :کل شار الکتریکی که از یک سطح بسته عبور میکند،
قانون گاوس :کل شار الکتریکی که از یک سطح بسته عبور میکند، Основные понятия электродинамики
Основные понятия электродинамики Демонтаж тормозной системы автомобиля
Демонтаж тормозной системы автомобиля Презентация на тему Энергосбережение в быту (8 класс)
Презентация на тему Энергосбережение в быту (8 класс) 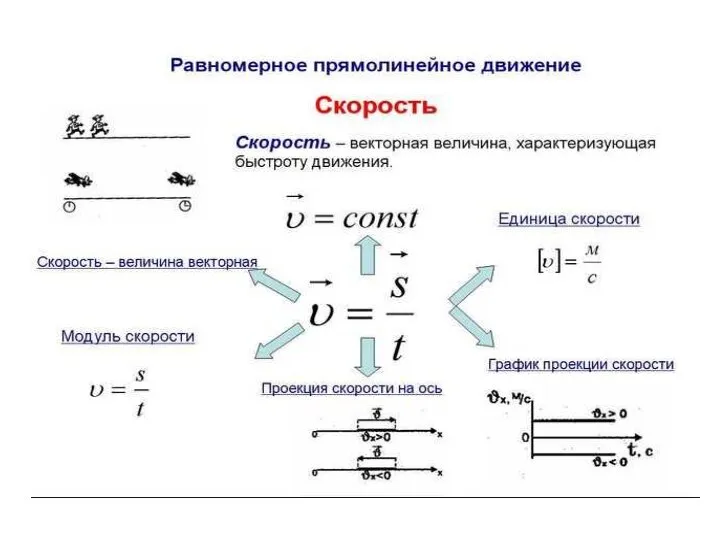 Равномерное прямолинейное движение
Равномерное прямолинейное движение Презентация по физике "Расчет стоимости электроэнергии. Электроприборы в быту. Техника электробезопасности" -
Презентация по физике "Расчет стоимости электроэнергии. Электроприборы в быту. Техника электробезопасности" -