Лекция 3 Электромагнитные переходные процессы электрических цепях

В электрической цепи может быть только электромагнитная энергия. Электромагнитная энергия имеет место при наличии электрического и магнитного полей. Запас энергии магнитного поля определяется током и потокосцеплением
( ), а электрического – напряжением и зарядом ( ). Следовательно, необходимым условием возникновения переходных процессов является наличие в электрической цепи индуктивностей и емкостей.
Переходные процессы вызываются любым изменением параметров элементов цепи: величин и фаз ЭДС, величин сопротивлений, индуктивностей и емкостей, конфигурации цепи и т.д. Наиболее часто переходные процессы вызываются коммутацией в цепи, происходящей при замыкании (рис. 1, а) или размыкании (рис. 1, б) выключателей.

Переходные процессы в электрических цепях являются быстро протекающими. Длительность их обычно не превышает долей секунды. Сравнительно редко переходные процессы продолжаются несколько секунд. Тем не менее, изучение переходных процессов необходимо. В результате переходных процессов деформируются по форме и амплитуде сигналы при прохождении их через усилители и другие устройства.

В промышленных электрических сетях возможно возникновение опасных для изоляции перенапряжений на отдельных участках цепи, увеличение амплитуд токов, которые могут в десятки раз превышать амплитуды токов установившегося режима, и т.д. Владение знаниями о природе переходных процессов позволяет предусмотреть мероприятия по предотвращению нежелательных явлений.

ЗАКОНЫ КОММУТАЦИИ И НАЧАЛЬНЫЕ УСЛОВИЯ
Для всех переходных процессов условимся, что момент t = 0 соответствует моменту коммутации. Тогда время t = 0– представляет собой момент времени непосредственно до коммутации, t = 0+ – непосредственно после коммутации.
Переход к новому режиму связан с изменением энергии в индуктивностях и емкостях цепи, которые не могут изменяться мгновенно. Энергия может изменяться только плавно, так как в противном случае мощность, равная производной энергии по времени, должна быть равна бесконечности, что физически невозможно. Поэтому размыкание индуктивности будет сопровождаться электрической дугой между контактами, в которой будет рассеиваться запасенная в индуктивности энергия. К аналогичному выводу приводит замыкание накоротко емкости.

Если исключить случаи размыкания индуктивности и замыкания накоротко емкости, то, считая, что коммутация происходит мгновенно, можно дугообразование не учитывать.
Первый закон (правило) коммутации.
Так как энергия, запасенная в индуктивности (WL = Ψ2/L, а Ψ = Li), мгновенно измениться не может, то при неизменной во времени индуктивности ток в ней не может измениться скачком. Т.е., ток через индуктивный элемент L непосредственно до коммутации iL(0 –) равен току через этот же индуктивный элемент непосредственно после коммутации iL(0+):
iL(0 –) = iL(0+) (1)

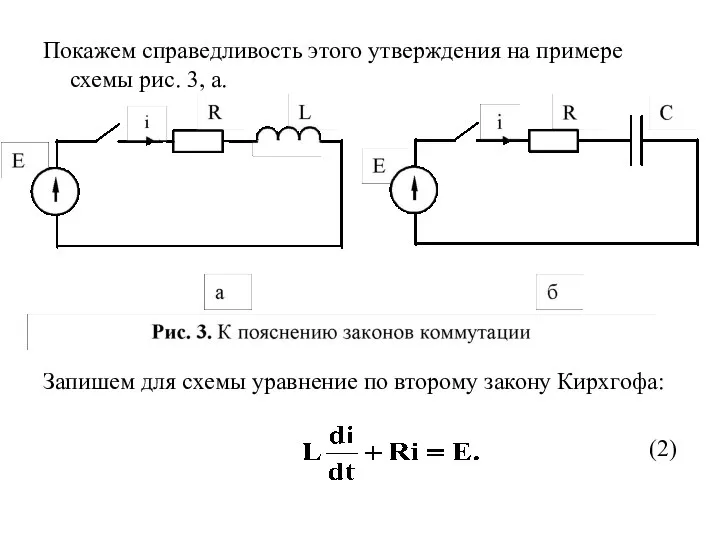
Покажем справедливость этого утверждения на примере схемы рис. 3, а.
Запишем для схемы уравнение по второму закону Кирхгофа:
(2)

Ток i и ЭДС Е могут принимать конечные (не бесконечно большие) значения.
Допустим, что ток i может измениться скачком. Скачок тока означает, что за бесконечно малый интервал времени Δt → 0 ток изменится на конечное значение Δi. При этом Δi/Δt → ∞ .
Если вместо в уравнение (2) подставить ∞, то его левая
часть не будет равна правой части и не будет соблюдаться второй закон Кирхгофа.
Допустим, что при переходных процессах второй закон Кирхгофа в цепи не действует, и рассмотрим выполнимость первого закона коммутации с энергетической точки зрения. При бесконечно большом напряжении и конечном изменении тока мгновенная мощность, выделяемая индуктивностью, будет равна бесконечности, что противоречит законам естествознания.

Ток через индуктивность не может изменяться скачком, но напряжение на индуктивности, равное , скачком измениться может. Это не противоречит второму закону Кирхгофа.
Энергия, запасенная в емкости (WС = q2/C, а q = Cu), мгновенно измениться не может, поэтому при неизменной во времени емкости напряжение на ней не может измениться скачком. Напряжение на емкости С непосредственно после коммутации uC(0+) равно напряжению на ней непосредственно до коммутации uC(0 –):
uC(0 –) = uC(0+) (3)
Справедливость этого утверждения доказывается аналогично тому, как это было сделано выше.
Рассмотрим цепь с конденсатором (рис. 3, б). По второму закону Кирхгофа:
, (4)

Так как то
(5)
Если допустить, что напряжение uC может измениться скачком, то
и левая часть выражения (5) не будет равна правой части.
При скачкообразном изменении напряжения происходит скачкообразное изменение энергии, что может быть только при бесконечно большой мощности. В природе такого быть не может.

Следовательно, допущение о возможности скачкообразного изменения напряжения на конденсаторе также противоречит законам естествознания. Однако ток через конденсатор,
равный может изменяться скачком, поскольку это
не противоречит второму закону Кирхгофа.

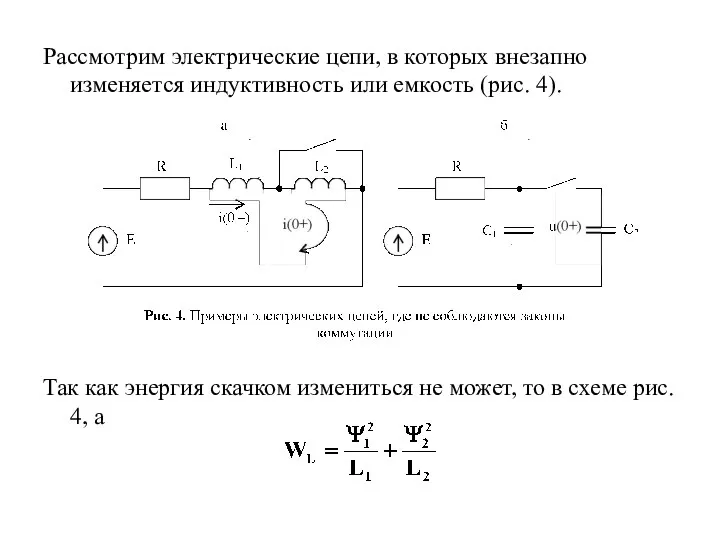
Рассмотрим электрические цепи, в которых внезапно изменяется индуктивность или емкость (рис. 4).
Так как энергия скачком измениться не может, то в схеме рис. 4, а

При неизменных во времени индуктивностях сумма потокосцеплений до и после коммутации должна остаться неизменной. Поэтому
(1а)
Аналогично, в схеме рис. 4, б имеем:
Откуда (3а)
Уравнения (1а) и (3а) отражают обобщенные первый и второй законы коммутации. Согласно первому обобщенному закону коммутации: потокосцепление в электрической цепи не может измениться скачком; согласно второму: электрический заряд в электрической цепи не может измениться скачком. Т.е., потокосцепление и заряд до коммутации равны соответственно потокосцеплению и заряду после коммутации.

Следует отметить, что обобщенные законы коммутации справедливы только для идеализированных электрических цепей, в которых индуктивности и емкости не имеют резистивных элементов. В действительности каждая индуктивная катушка имеет активное сопротивление, а каждая емкость – активную проводимость. Кроме того, проводники, соединяющие эти элементы, всегда имеют активное сопротивление, и обязательно коммутации в таких цепях будут сопровождаться электрической дугой. Поэтому в действительности при коммутации выполняются законы, выраженные уравнениями (1) и (3). Но такой переходный процесс можно рассматривать как состоящий из двух стадий: первая очень короткая, в результате которой устанавливаются одинаковые токи в последовательно включенных индуктивностях и напряжения на параллельно включенных емкостях; и вторая по времени на порядки большая, определяемая изменением энергии в цепи. Ввиду несоразмерности времен первой стадией переходного процесса пренебрегают, а токи через индуктивности и напряжения на емкостях определяют из (1а) и (3а).

Независимые и зависимые, нулевые и ненулевые начальные условия.
Под начальными условиями (или начальными значениями) понимают значения токов и напряжений в схеме непосредственно после коммутации – при t = 0+.
Ранее было установлено, что токи через индуктивные элементы и напряжения на конденсаторах в момент времени непосредственно после коммутации равны своим значениям в момент времени непосредственно до коммутации. Остальные величины, такие как напряжения на индуктивных элементах и резисторах, токи через конденсаторы и резисторы могут изменяться скачком, и поэтому их значения после коммутации чаще всего отличаются от значений до коммутации. Поэтому принято выделять послекоммутационные начальные условия, которые принято называть начальными условиями.

С этой целью значения токов в ветвях, содержащих индуктивные элементы, и значения напряжений на конденсаторах берут равными тем значениям, которые они имели до коммутации при t = 0 –, а остальные токи и напряжения после коммутации при t = 0+ находят из уравнений Кирхгофа, поскольку часть слагаемых в них известна.
Значения токов через индуктивные элементы и напряжений на конденсаторах, известных из докоммутационного режима, условимся называть независимыми начальными значениями.
Значения остальных токов и напряжений при t = 0+ в схеме после коммутации, которые определяются по независимым начальным значениям из законов Кирхгофа, будем называть зависимыми начальными значениями.

Неизменности токов через индуктивности и напряжений на емкостях в момент коммутации можно использовать для определения токов и напряжений в цепи непосредственно после коммутации. Для этого достаточно в схеме замещения индуктивности заменить источниками токов, а емкости – источниками ЭДС. В результате этого в схеме исключаются индуктивности и емкости и остаются одни сопротивления. Это очень упрощает расчет, особенно если в цепи действуют не постоянные источники электрической энергии.

Пример. В цепи (рис. 5а) действует постоянная ЭДС Е = 100 В. Сопротивления соответственно равны: R1 = 15 Ом; R2 = 10 Ом. До коммутации весь ток в цепи протекает через индуктивность: i3 = 4 А. Чтобы рассчитать начальные условия, заменим индуктивность источником тока, равным 4 А, а емкость закоротим, так как напряжение на ней до коммутации равно нулю. На рис. 5, б Схема для расчета послекоммутационных токов и напряжений изображена.

При нулевых начальных условиях токи в индуктивных элементах и напряжения на конденсаторах начнут изменяться с нулевых значений, при ненулевых условиях – с тех значений, которые они имели непосредственно до коммутации.
При нулевых начальных условиях, когда uC(0 –) = 0 и iL(0 –) = 0, индуктивность непосредственно после коммутации можно представить разрывом цепи, а емкость сопротивлением, равным нулю.

ПРИНУЖДЕННЫЕ И СВОБОДНЫЕ СОСТАВЛЯЮЩИЕ ТОКОВ И НАПРЯЖЕНИЙ
Выражение (2) представляет собой уравнение, записанное по второму закону Кирхгофа для схемы рис. 3, а при замкнутом ключе. Решением этого дифференциального уравнения будет величина тока, протекающего в рассматриваемой цепи.
Общее решение линейного дифференциального уравнения есть сумма частного решения неоднородного уравнения и общего решения однородного уравнения. Частное решение уравнения электрической цепи определяется только действием источников электрической энергии и не учитывает запасенные энергии в индуктивностях и емкостях. Частное решение уравнения (2) равно E/R (Е – постоянная ЭДС) – величина тока, установившегося в цепи по окончании переходного процесса.

Однородное уравнение получается из исходного, если его правую часть приравнять нулю. Решение однородного уравнения определяется только изменением запасенной энергии в электрической цепи, т.е., энергиями в индуктивностях и емкостях. В нашем случае однородное уравнение имеет вид:
. (6)
Решением однородного уравнения является показательная функция вида А еpt.
Постоянные А и р не зависят от времени. Без вывода дадим их значения для рассматриваемого примера: А = –E/R и р = – R/L. Следовательно, решение уравнения (2) запишется так:
, (7)

где E/R – частное решение неоднородного уравнения (2);
– общее решение однородного уравнения (2).
Частное решение неоднородного дифференциального уравнения называют принужденной составляющей тока (напряжения), а полное решение однородного уравнения – свободной составляющей. Применительно к рассмотренному примеру принужденная составляющая тока iпр = E/R, а свободная составляющая
Полный ток в цепи равен сумме принужденной и свободной составляющих тока:
i =iпр+iсв. (8)

Принужденная составляющая тока (напряжения) физически представляет собой составляющую, изменяющуюся с той же частотой, что и действующие в схеме источники электрической энергии. Если в схеме действует принуждающая синусоидальная ЭДС частоты ω, то принужденная составляющая любого тока и любого напряжения является соответственно синусоидальным током (синусоидальным напряжением) той же частоты ω.
Принужденные составляющие в цепи синусоидального тока определяются с помощью символического метода. Если в схеме действует источник постоянной ЭДС, то принужденный ток есть постоянный ток и находят его с помощью методов, рассмотренных в первой части ТОЭ.

В линейных электрических цепях свободные составляющие токов и напряжений затухают во времени по показательному закону ept.
Так, в рассмотренном примере . С увеличением
времени t множитель е–R/L быстро уменьшается. Название «свободная» объясняется тем, что эта составляющая есть решение уравнения, свободного от вынуждающей силы (однородного уравнения без правой части). С физической точки зрения свободные составляющие токов и напряжений определяются изменением запасенной энергии в цепи – магнитного поля в индуктивностях и электрического поля – в емкостях.

Принужденные и свободные составляющие токов и напряжений во время переходного процесса являются только расчетными компонентами, сумма которых дает действительные величины. Полный ток ветви является тем током, который в действительности протекает по ветви при переходном процессе. Точно так же, полное напряжение – это напряжение, которое в действительности имеется между некоторыми точками электрической цепи при переходном процессе.

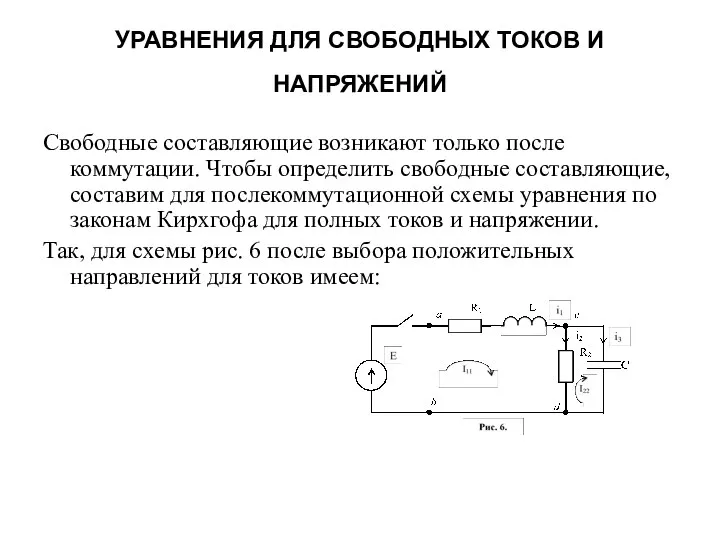
УРАВНЕНИЯ ДЛЯ СВОБОДНЫХ ТОКОВ И НАПРЯЖЕНИЙ
Свободные составляющие возникают только после коммутации. Чтобы определить свободные составляющие, составим для послекоммутационной схемы уравнения по законам Кирхгофа для полных токов и напряжении.
Так, для схемы рис. 6 после выбора положительных направлений для токов имеем:

Принужденные и свободные составляющие токов и напряжений во время переходного процесса являются только расчетными компонентами, сумма которых дает действительные величины. Полный ток ветви является тем током, который в действительности протекает по ветви при переходном процессе. Точно так же, полное напряжение – это напряжение, которое в действительности имеется между некоторыми точками электрической цепи при переходном процессе.

В этих уравнениях i1, i2 и i3 – полные токи. Каждый из них состоит из свободного и принужденного токов. Для того чтобы от этой системы уравнении перейти к уравнениям для свободных токов, «освободим» систему от вынуждающих ЭДС (в нашем случае от ЭДС Е) и вместо i1 запишем i1св, вместо i2 – i2св и т. д. В результате получим:

(9)
Нулевые значения правой части системы уравнений (9) свидетельствуют о том, что в схеме замещения для свободных токов и напряжений отсутствуют источники электрической энергии.
В схеме замещения для свободных токов и напряжений отсутствуют только величины ЭДС и токов источников электрической энергии, а ветви с внутренними сопротивлениями источников остаются. Внутреннее сопротивление источника ЭДС равно нулю, а источника тока – бесконечности. Поэтому источник ЭДС в схеме замещается сопротивлением, равным нулю, а ветвь с источником тока исключается.
Для свободных токов и напряжений любой электрической цепи соблюдаются первый и второй законы Кирхгофа.

АЛГЕБРАИЗАЦИЯ СИСТЕМЫ УРАВНЕНИЙ ДЛЯ СВОБОДНЫХ ТОКОВ
Уравнение для каждой свободного тока можно представить в виде iсв = Аеpt.
Постоянная интегрирования А для каждого свободного тока своя. Показатели же затухания р одинаковы для свободных токов ветвей. Физически это объясняется тем, что вся цепь охвачена единым (общим) переходным процессом и характер изменения составляющих полной энергии цепи (в индуктивностях и емкостях) повторяет характер изменения полной энергии.
Запишем производную от свободного тока:

Следовательно, производную от свободного тока можно заменить на piсв, а свободное напряжение на индуктивном элементе L – на Lpсв. Найдем интеграл от свободного тока:
Постоянная интегрирования взята здесь равной нулю, так как свободные составляющие не содержат не зависящих от времени слагаемых.
Следовательно, интеграл от свободного тока можно заменить на iсв/p, а свободное напряжение на конденсаторе
на

После подстановки полученных значений в уравнения (9) получим систему алгебраических уравнений относительно свободных составляющих токов i1cв, i2cв и i3cв:
(10)
Переход от системы линейных дифференциальных уравнений к системе алгебраических уравнений называют алгебраизацией системы дифференциальных уравнений для свободных токов. Можно сказать, что система (10) есть результат алгебраизации системы дифференциальных уравнений (9).

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ
Число алгебраических уравнений равно числу неизвестных свободных токов. Положим, что р известно и решим систему (10) относительно i1cв, i2cв и i3cв.
где D – определитель системы:

Определитель Δ1 получим из выражения для Δ, заменив элементы первого столбца столбцом свободных членов системы (10) и т. д.
Так как правая часть системы (10) всегда нулевая, то в каждом определителе Δ1, Δ2 и Δ3 один из столбцов будет состоять из нулей.
Известно, что если в определителе один из столбцов состоит из нулей, то этот определитель равен нулю. Следовательно, Δ1 = 0, Δ2 = 0, Δ3 = 0.

Из физических соображений ясно, что каждый из свободных токов не может быть равен нулю, ибо в этом случае не будут выполнены законы коммутации. Однако, если
то
Следовательно, свободные токи могут быть не равны нулю только в том случае, когда определитель системы
Δ = 0 (11)

Таким образом, определитель D алгебраизованной системы уравнений должен равняться нулю.
Уравнение Δ = 0 называют характеристическим уравнением. Единственным неизвестным в нем является р.
Характеристическое уравнение составляется для послекоммутационной схемы.
Решение для свободного тока берется в экспоненциальном виде Aept. Если характеристическое уравнение имеет не один корень, а несколько, например n, то для каждого свободного тока (напряжения) нужно взять сумму

СОСТАВЛЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ ПУТЕМ ИСПОЛЬЗОВАНИЯ ВЫРАЖЕНИЯ ДЛЯ ВХОДНОГО СОПРОТИВЛЕНИЯ ЦЕПИ НА ПЕРЕМЕННОМ ТОКЕ
Уравнения состояния электрической цепи записывается не только через уравнения Кирхгофа. Отсутствие в схеме замещения для определения свободных контурных токов и напряжений в узлах источников электрической энергии является причиной того, что частные определители, составленные для контурных токов и узловых напряжений, равны нулю. Следовательно, ненулевые значения контурных токов и напряжений в узлах могут быть только тогда, когда главный определитель будет равен нулю. Покажем это на примере уравнений контурных токов. Определитель системы уравнений для определения контурных токов схемы изображенной на рис. 6, запишется как:

Характеристическое уравнение будет таким же, как и полученное из системы уравнений, составленных по законам Кирхгофа.
Можно получить характеристическое уравнение, взяв за основу не метод контурных токов, а метод узловых потенциалов. В этом случае следует приравнять нулю определитель матрицы узловых проводимостей, полагая при составлении матрицы один из узлов схемы заземленным.

Характеристическое уравнение для определения р часто составляют более простым способом, чем рассмотренные. С этой целью разрывают любую ветвь и составляют выражение входного сопротивления двухполюсника на переменном токе, обозначив его как Z(jω), заменяют в нем jω на p [получают Z(p)] и приравнивают Z(p) нулю. Сопротивление, приравненное Z(p) называется операторным.
Уравнение Z(p) = 0 совпадает с характеристическим, полученным через уравнения, составленные на основании законов Кирхгофа, контурных токов, узловых напряжений и др.
Еще раз подчеркнем, что при составлении характеристического уравнения ветви с внутренними сопротивлениями источников остаются.

ОПРЕДЕЛЕНИЕ СТЕПЕНИ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Степень характеристического уравнения равна числу независимых начальных условий. Как правило, это суммарное количество индуктивностей и емкостей схемы замещения электрической цепи. Это позволяет в какой-то мере контролировать расчет.
Однако в некоторых случаях число независимых начальных условий может оказаться меньше суммарного количества индуктивностей и емкостей. Например, схема на рис. 7,а содержит три индуктивных элемента и один емкостный.

Составим характеристическое уравнение для этой схемы, записав выражение для операторного входного сопротивления:

Характеристическое уравнение будет иметь вид:
и имеет третью степень, несмотря на то, что в схеме четыре реактивных элемента. Объясняется это тем, что ток в одной из индуктивностей дополняет до нуля алгебраическую сумму токов узла, созданного тремя индуктивностями, и не является независимым. Поэтому из четырех начальных условий, определяемых количеством индуктивностей и емкостей, три являются основными и одно – неосновным.
На одно независимое условие будет меньше количества емкостей в электрической цепи, изображенной на рис 7, б, так как напряжение на одной из емкостей дополняет до нуля алгебраическую сумму напряжений контура, созданного из четырех емкостей.

Не увеличится степень характеристического уравнения, если в схеме имеются последовательно или параллельно включенные индуктивности или емкости, которые можно заменить одной эквивалентной. Поэтому при определении степени характеристического уравнения следует, во-первых, произвести замену последовательно и параллельно включенных индуктивностей, емкостей соответственно эквивалентными, во-вторых, выделить узлы, все ветви которых имеют индуктивности, и контуры, состоящие только из емкостей. Степень характеристического уравнения будет меньше суммы индуктивностей и емкостей на суммарное количество таких узлов и контуров.

СВОЙСТВА КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Число корней характеристического уравнения равно степени этого уравнения, которая в свою очередь равна числу независимых начальных условий. Если характеристическое уравнение представляет собой уравнение первой степени, то оно имеет один корень, если второй степени – два корня и т. д. Уравнение первой степени имеет всегда отрицательный действительный (не мнимый и не комплексный) корень.
Уравнение второй степени может иметь:
два действительных неравных отрицательных корня;
два действительных равных отрицательных корня;
два комплексно–сопряженных корня с отрицательной действительной частью.

Уравнение третьей степени может иметь:
три действительных неравных отрицательных корня; три действительных отрицательных корня, из которых два равны друг другу;
три действительных равных отрицательных корня;
один действительный отрицательный корень и два комплексно-сопряженных с отрицательной действительной частью.
Действительные части корней характеристических уравнений всегда отрицательные, Так как свободный процесс, описываемый слагаемыми вида Аеpt, происходит в цепи, не содержащей источников энергии. Следовательно, свободные токи должны затухать во времени, и действительная часть показателя экспоненты р обязана быть отрицательной.

ЗАВИСИМОСТЬ ХАРАКТЕРА ПЕРЕХОДНОГО
ПРОЦЕССА ОТ ЧИСЛА КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Характер свободного процесса при одном корне
Когда характеристическое уравнение имеет один корень, свободный ток описывается выражением
(14)
где р = – а зависит только от параметров цепи, А — от параметров цепи, ЭДС и момента включения. Характер изменения iCB при А >0 показан на рис. 8.
За интервал времени t = τ = 1/а функция Aе–at уменьшится в е раз.
Величину τ = 1/а = 1/|р| называют постоянной времени цепи; Постоянная времени зависит только от вида и параметров пассивных элементов цепи, но не зависит от величин ЭДС и источников тока. Так, для цепи рис. 3a τ = L/R, для цепи рис. 3 б, τ = RС и т.д.

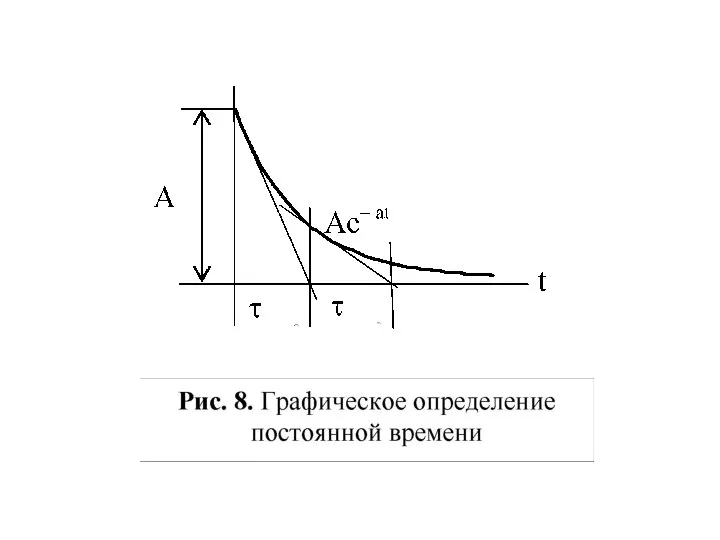
Название «постоянная времени» отражает постоянство подкасатель­ной к экспоненте в любой момент времени: подкасательная к экспоненте е–t/τ численно равна τ (см. рис. 6).
Переходный процесс практически заканчивается за время, равное 5τ. Действительно, через τ свободная составляющая уменьшится до 0,368 от значения при t = 0, через 2τ – до 0,135, через 3τ – до 0,05, через 4τ – до 0,018, через 5τ – до 0,00674. Поэтому полная картина расчетов переходных процессов в электрической цепи с несколькими индуктивностями и емкостями получается, если время расчета примерно равно пятикратной максимальной постоянной времени, получаемой как tmax = 1/|рmin|.

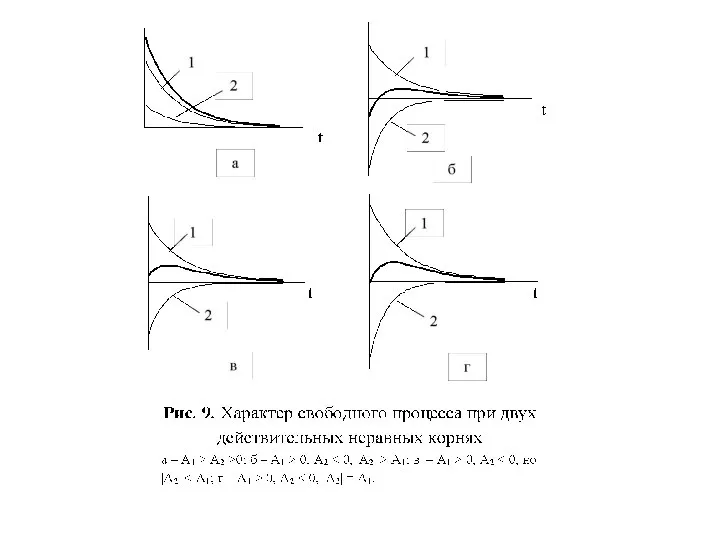
Характер свободного процесса
при двух действительных нерав­ных корнях
Пусть p1 = – a, p2 = – b (для определенности положим b >а). Тогда
(15)
Характер изменения свободного тока при различных по значению и знаку постоянных интегрирования A1 и A2, качественно иллюстрируется кривыми рис. 9, а – г; кривая 1 представляет собой функцию A1е–at, кривая 2—функцию A2е–bt, результирующая кривая получена путем суммирования ординат кривых 1 и 2. Для рис. 9, а A1 > A2 >0; для рис. 9, б A1 > 0, A2 < 0, |A2| > A1; для рис. 9, в A1 > 0, A2 < 0, но |A2| < A1; для рис. 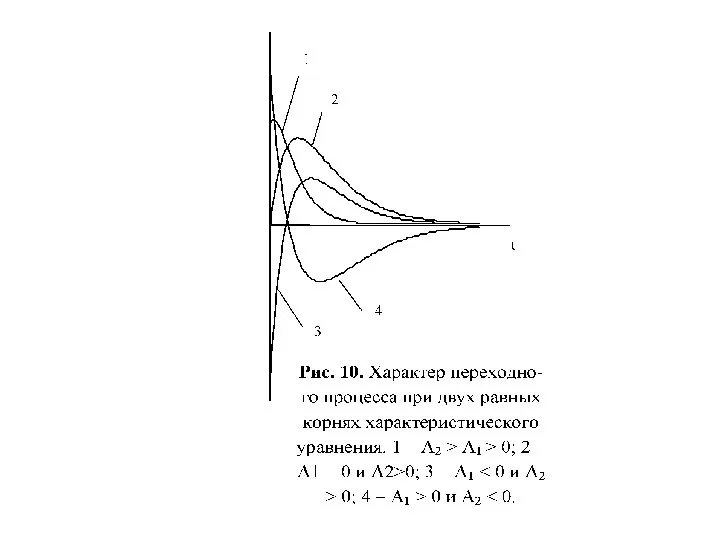9, г A1 > 0, A2 < 0, |A2| = A1.

Характер свободного процесса при двух равных корнях
Общее решение однородного дифференциального уравнения с равными корнями записывается как
(16)
На рис. 10 построены несколько кривых, показывающих возможный характер изменения функции при различных значениях постоянных интег­рирования, а также при равенстве нулю одной из постоянных.
Кривая 1 построена при А2 > А1 > 0; кривая 2 — при А1 = 0 и А2 > 0; кривая 3— при А1 < 0 и А2 > 0; кривая 4 — при А1 > 0 и А2 < 0.

Характер свободного процесса при двух комплексно – сопряженных корнях
Комплексные корни всегда являются попарно сопряженными. Так, если р1 = – δ + jω0t, то р2 = – δ – jω0t.
Соответствующее этим слагаемым решение имеет вид:
(17)
где