Операторы

Операторы
В квантовой физике многие физические величины могут квантоваться, т.е. в некоторых случаях они принимают лишь дискретные значения. Для математического описания таких величин не пригодны обычные непрерывные функции, используемые в классической теории. Квантовая теория использует более общие математические методы, основой которых являются операторы.

Операторы
Оператор − это математический символ, определяющий совокупность действий, которые надо провести над заданной функцией U для получения некоторой другой функции V. В общем случае будем обозначать оператор символом , изображая его действие на некоторую функцию U в виде произведения . В итоге оператор определяется соотношением:
Наибольший практический интерес представляют линейные операторы, удовлетворяющие условию:
C1 и C2 − произвольные постоянные

Операторы
Самосопряженный линейный оператор должен удовлетворять соотношению:
− оператор, комплексно – сопряженный
Операторы можно складывать, вычитать и перемножать по правилам обычной алгебры. Однако при перемножении нельзя менять порядок сомножителей.

Собственное значение оператора
В ряде случаев воздействие оператора на некоторую функцию U(x) эквивалентно умножению этой функции на постоянную L. Эта постоянная и называется собственным значением оператора
функция U(x), удовлетворяющая этому соотношению, называется собственной функцией данного оператора

Собственное значение оператора
В случае линейного дифференциального оператора уравнение
является линейным дифференциальным уравнением. Известно, что такое уравнение для заданных граничных условий имеет ненулевые решения лишь при определенных значениях L. Эти постоянные и являются собственными значениями оператора.
Дифференциальный оператор, как правило, имеет множество собственных значений и собственных функций. Совокупность всех собственных значений образует спектр, который может быть как сплошным, так и дискретным.

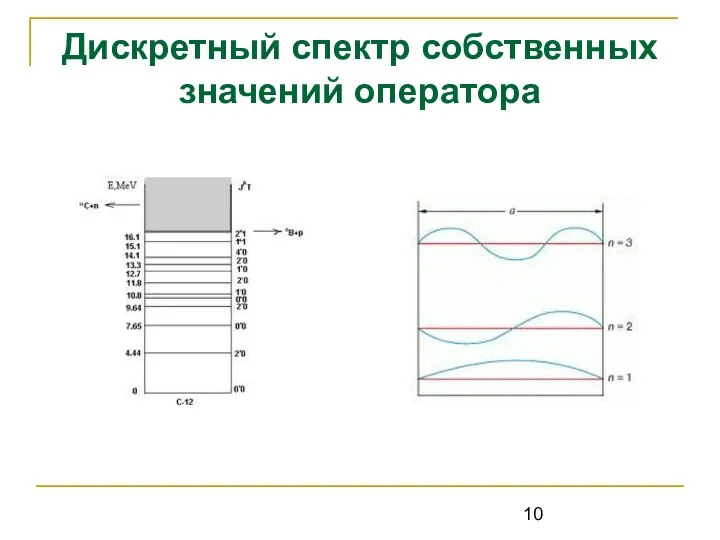
Дискретный спектр собственных значений оператора
С примером дискретного спектра встречаемся, решая, например, задачу о движении частицы между двумя отражающими плоскостями (или о модах планарного оптического волновода).
Пусть частица движется вдоль оси х между плоскостями х=0 и x=a. Полагаем, что потенциальная энергия U частицы при 0

Дискретный спектр собственных значений оператора
при (0 ≤ x < a)
В точках x=0; x=a функция ψ обращается в 0 (поскольку стенки − идеально отражающие, то вероятность нахождения на них частицы равна нулю). Решение этого уравнения ищем в виде:
где

Исходя из граничных условий
Дискретный спектр собственных значений оператора
найдем:
A = 0;
где n=1, 2, 3, … Тогда:
Таким образом, полная энергия частицы в данной задаче может принимать лишь дискретные значения Wn, соответствующие различным значениям n. Эти значения образуют бесконечный ряд дискретных энергетических уровней. При переходе частицы из одного состояния в другое, ее энергия должна меняться скачком, т.е. в данной ситуации имеет место квантование энергии.

Дискретный спектр собственных значений оператора

Гармонический осциллятор
Любая система, совершающая гармонические колебания с малой амплитудой вблизи состояния устойчивого равновесия (атом в молекуле, электрон в атоме, математический маятник и т.д.) представляет собой гармонический осциллятор.
Рассмотрим частицу с массой m, смещенную на некоторое малое расстояние относительно положения устойчивого равновесия. На частицу действует возвращающая упругая сила. Считая, что частица движется вдоль прямой, уравнение ее движения можно записать в виде:

Гармонический осциллятор
Здесь x – отклонение частицы от положения равновесия;
- упругая сила, возвращающая ее в это положение;
α – величина, называемая коэффициентом упругости.
Решение уравнения
при α=const:

в вещественной форме имеет вид:
Видим, что в указанных условиях частица совершает около положения равновесия гармонические колебания с частотой, определяемой только физическими параметрами m и α:
Гармонический осциллятор

Гармонический осциллятор
Модель гармонического осциллятора применима к любой системе, совершающей гармонические колебания с малой амплитудой вблизи состояния устойчивого равновесия (атом в молекуле, электрон в атоме, математический маятник и т.д.).
Покажем, что энергия осциллятора в силовом поле не может принимать любые значения, она оказывается квантованной.

Гармонический осциллятор
Полная энергия осциллятора в силовом поле, как отмечалось, равна:
где
Потенциальная энергия U связана с действующей на частицу силой F соотношением:
В нашем одномерном случае:

Гармонический осциллятор
Интегрируя это соотношение, найдем U:
Полагая С=0 (константа интегрирования в каждой конкретной задаче определяется начальными условиями), получим:
И найдем полную энергию осциллятора

Гармонический осциллятор
Состояние гармонического осциллятора с точки зрения квантовой теории характеризуется волновой функцией ψ, удовлетворяющей уравнению Шредингера:

Гармонический осциллятор
Решение этого уравнения хорошо исследовано. Оно является конечным и однозначным (как отмечалось, волновая функция должна отвечать таким условиям) на интервале при дискретных значениях постоянной W:
где n = 0, 1, 2,… – любое целое число.

Гармонический осциллятор
Так, энергия гармонического осциллятора, находящегося в поле потенциальных сил, может принимать только дискретные значения и при изменении его состояния изменяется скачком на величину, кратную энергии кванта hω.
Наименьшая величина энергии гармонического осциллятора:
Она называется нулевой энергией гармонического осциллятора.