Содержание
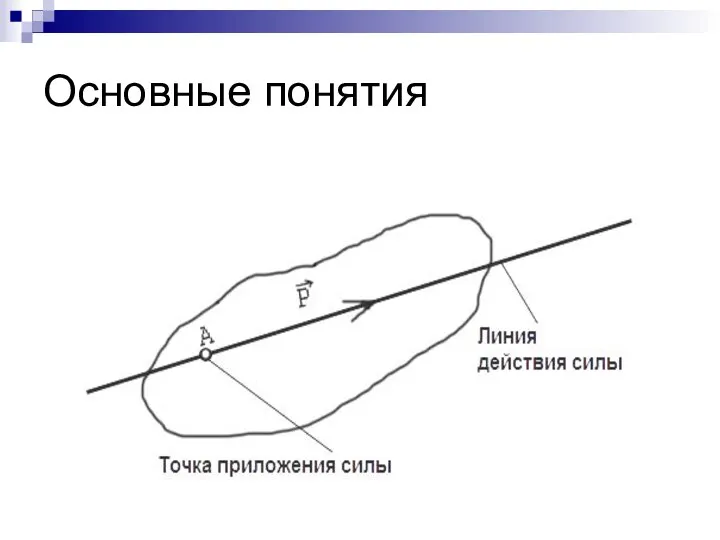
- 2. Основные понятия
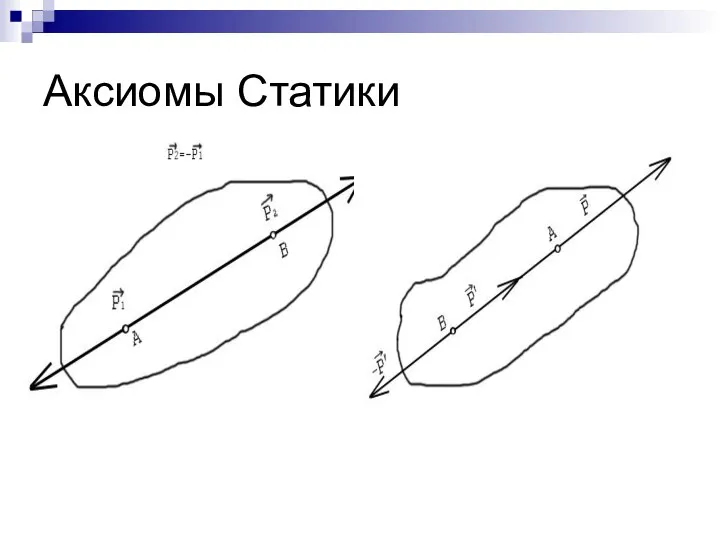
- 3. Аксиомы Статики
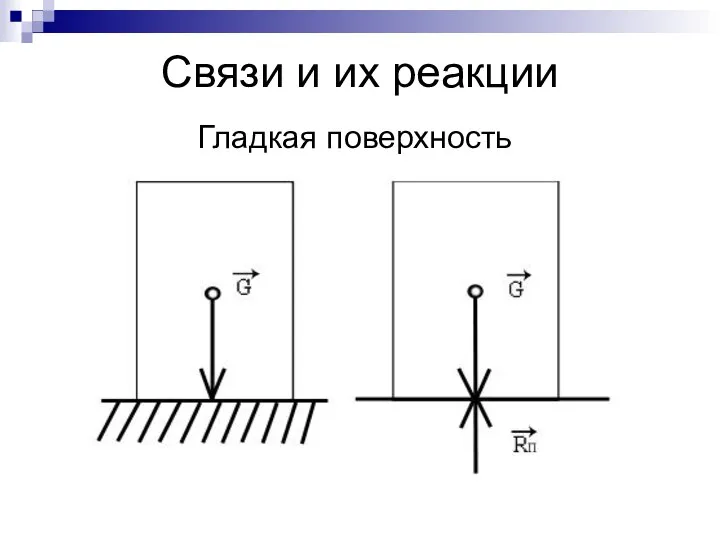
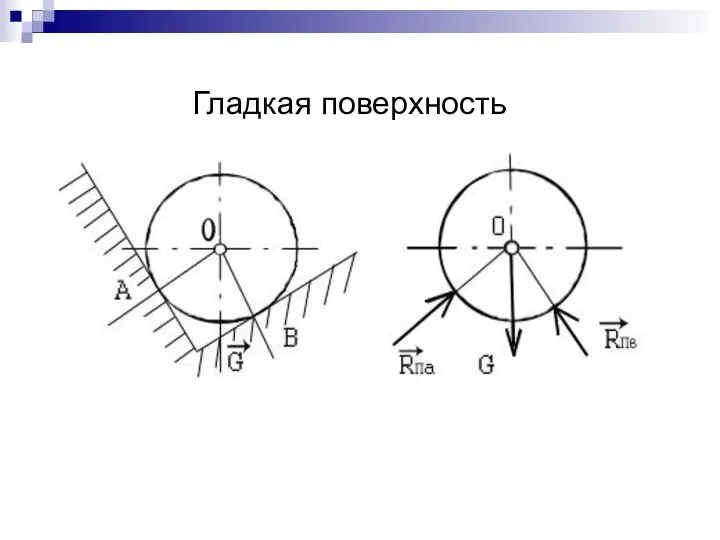
- 5. Связи и их реакции Гладкая поверхность
- 6. Гладкая поверхность
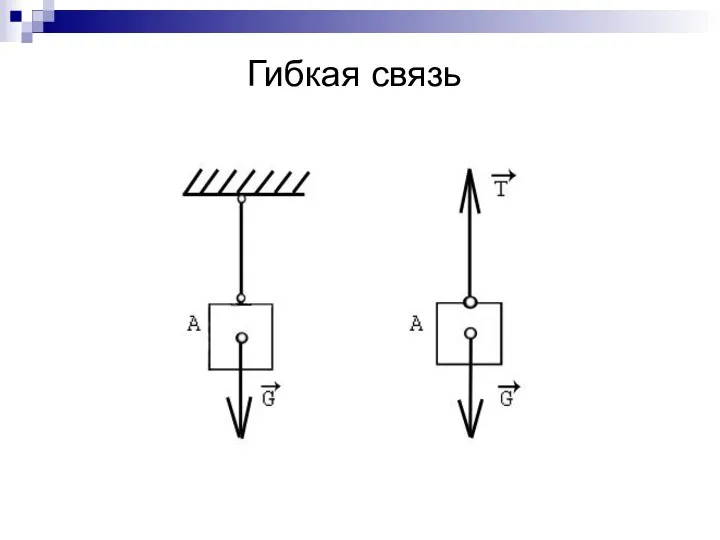
- 7. Гибкая связь
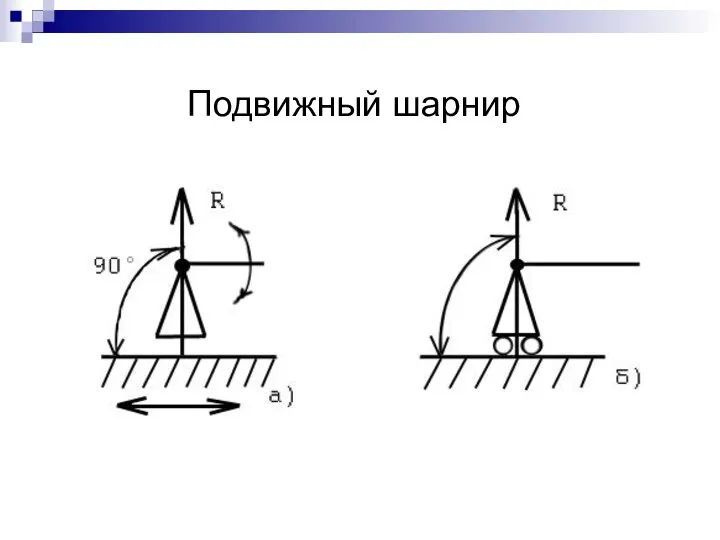
- 8. Подвижный шарнир
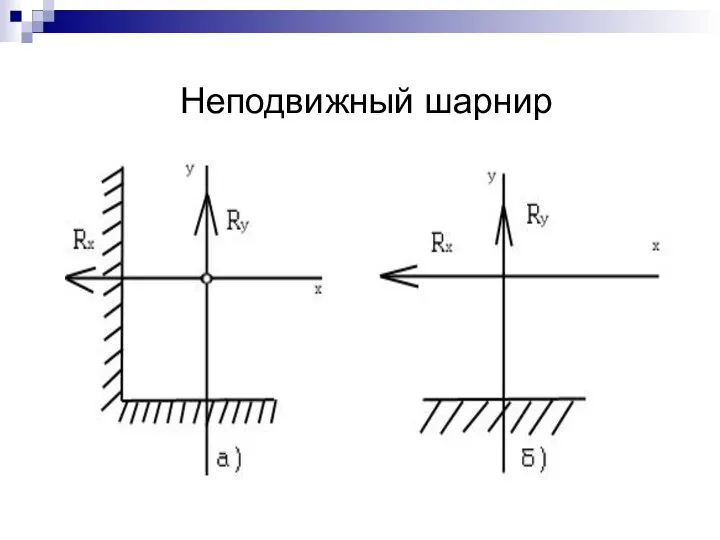
- 9. Неподвижный шарнир
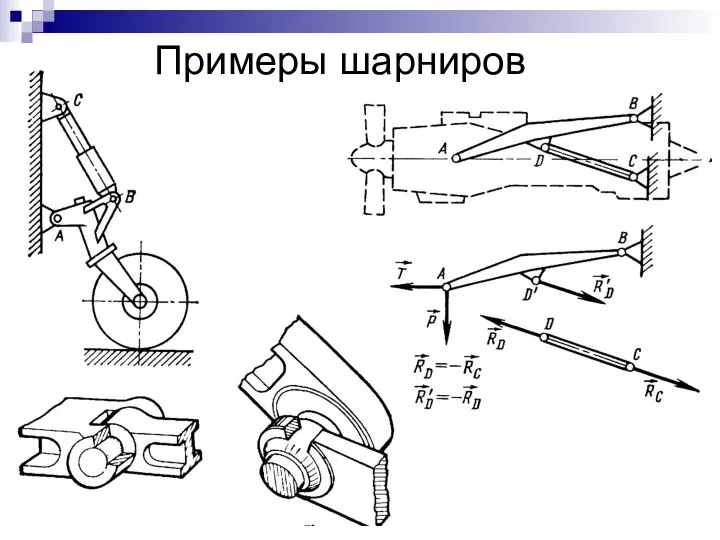
- 10. Примеры шарниров
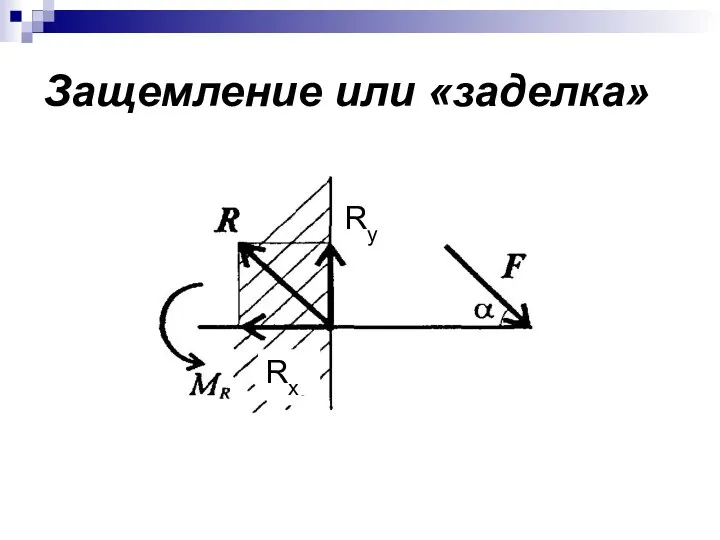
- 11. Защемление или «заделка» Ry Rx
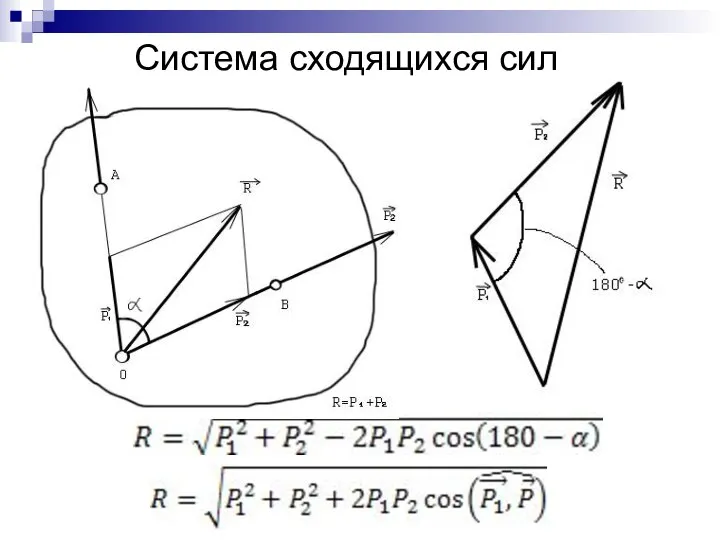
- 12. Система сходящихся сил
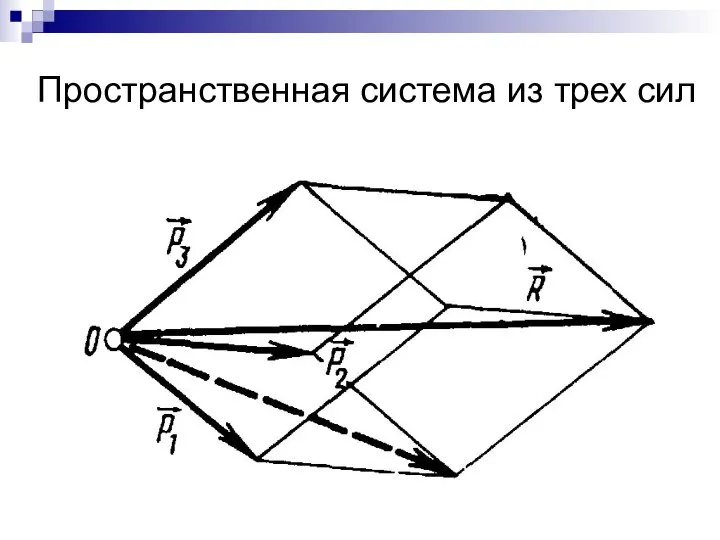
- 13. Пространственная система из трех сил
- 15. Равновесие системы сходящихся сил
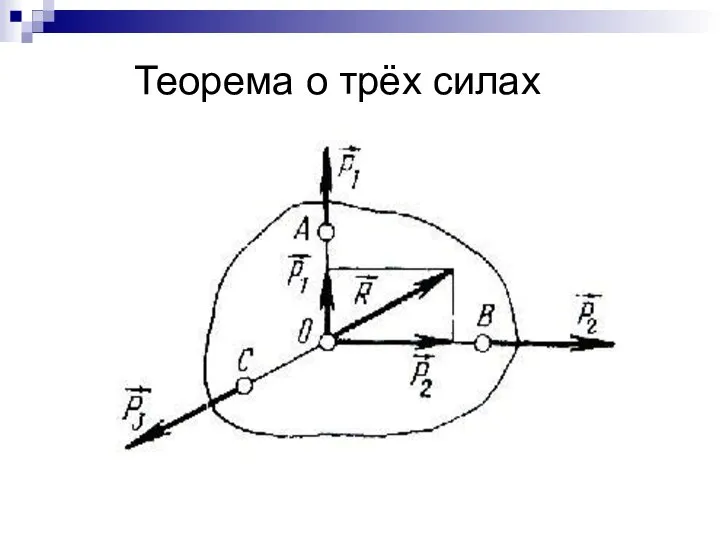
- 16. Теорема о трёх силах
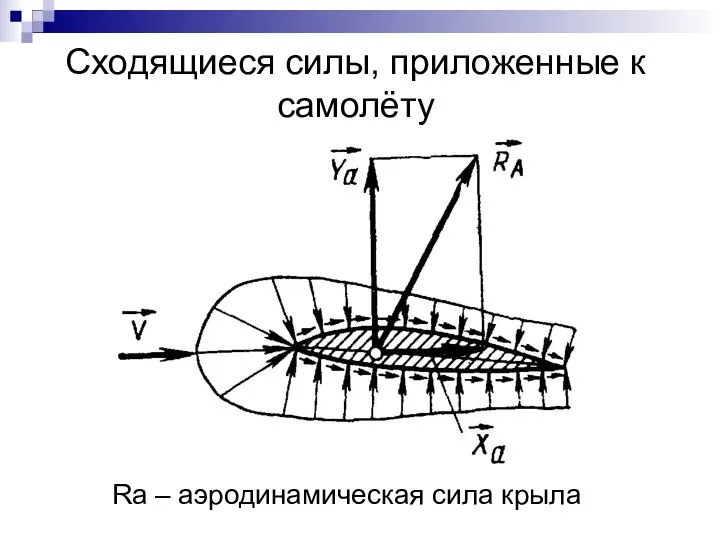
- 17. Сходящиеся силы, приложенные к самолёту Ra – аэродинамическая сила крыла
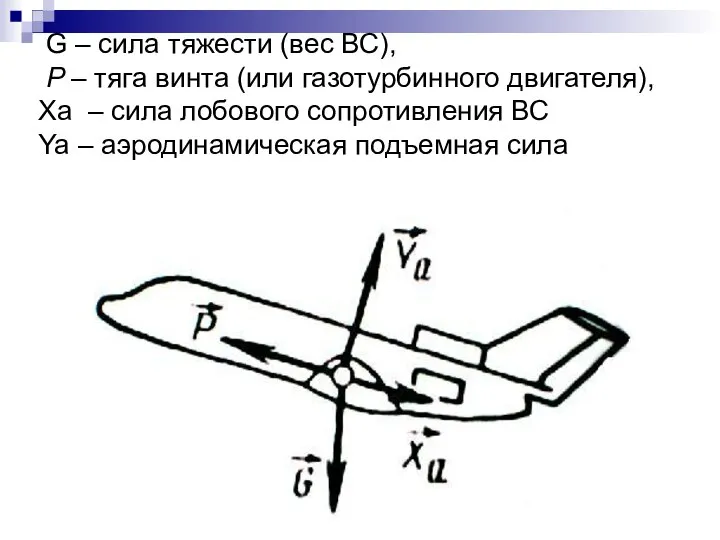
- 18. G – сила тяжести (вес ВС), P – тяга винта (или газотурбинного двигателя), Xa – сила
- 19. Теорема Вариньона о моменте равнодействующей сходящейся системы сил
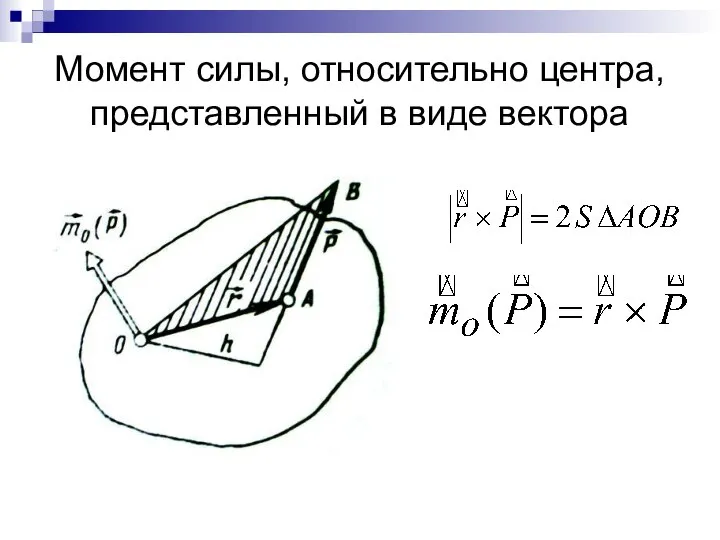
- 20. Момент силы, относительно центра, представленный в виде вектора
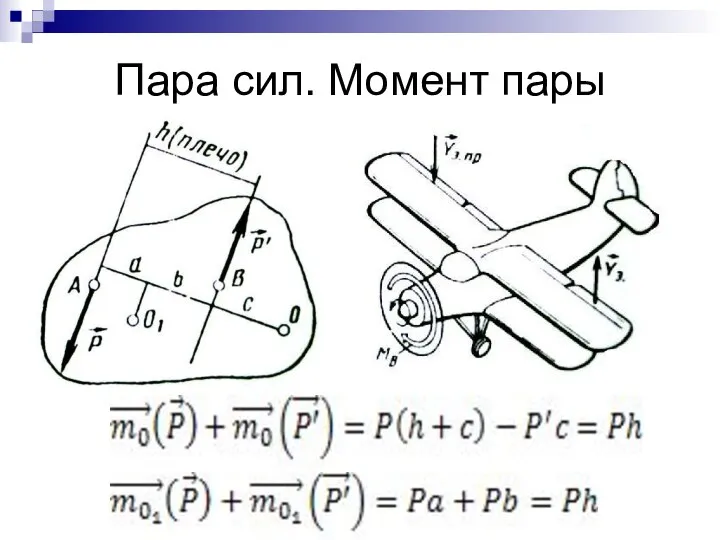
- 22. Пара сил. Момент пары
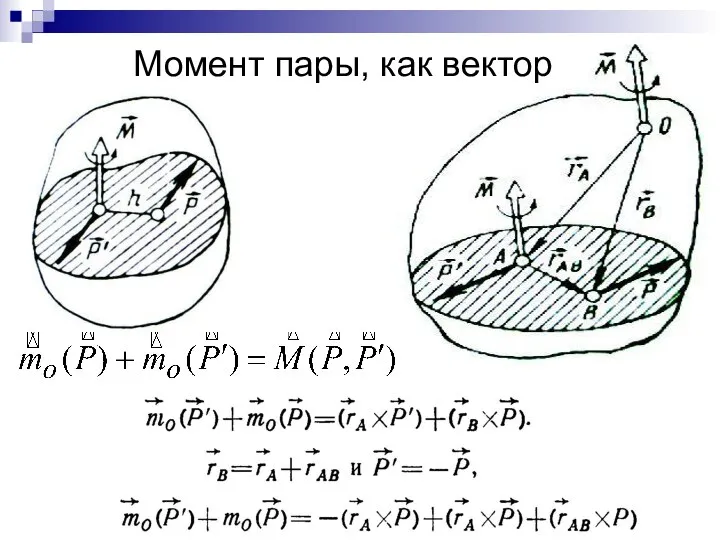
- 23. Момент пары, как вектор
- 24. Сложение пар. Равновесие тела под действием системы пар
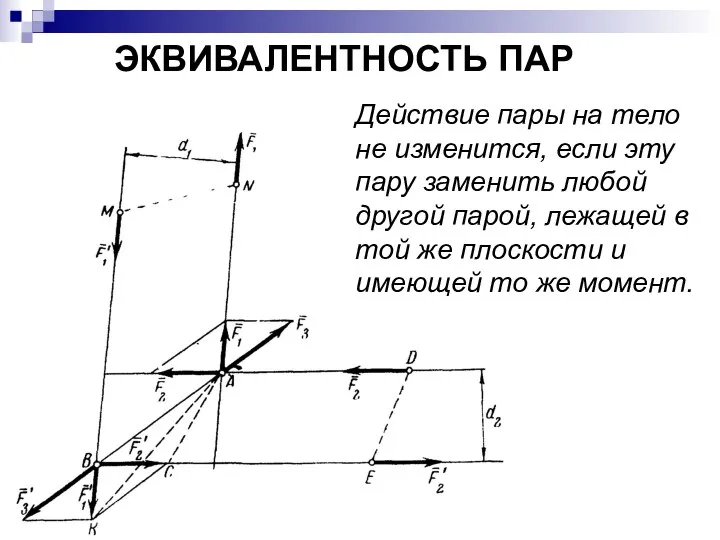
- 25. ЭКВИВАЛЕНТНОСТЬ ПАР Действие пары на тело не изменится, если эту пару заменить любой другой парой, лежащей
- 26. Свойства пары сил: 1. Действие пары на тело не изменится, если переместить пару в другое положение
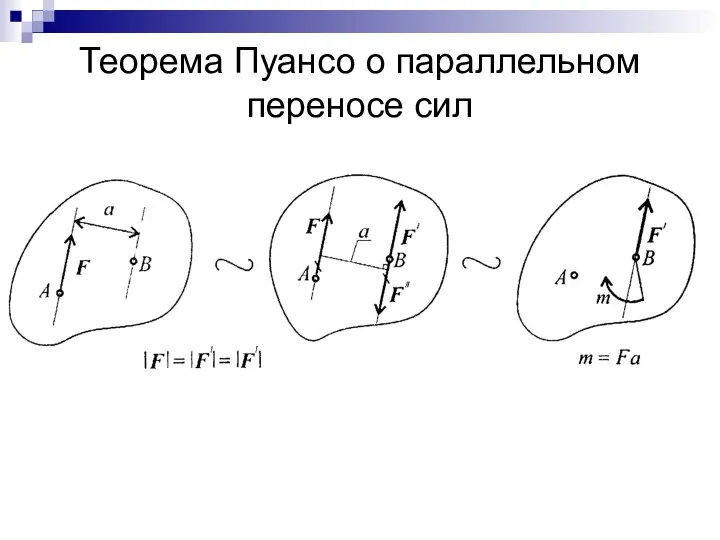
- 27. Теорема Пуансо о параллельном переносе сил
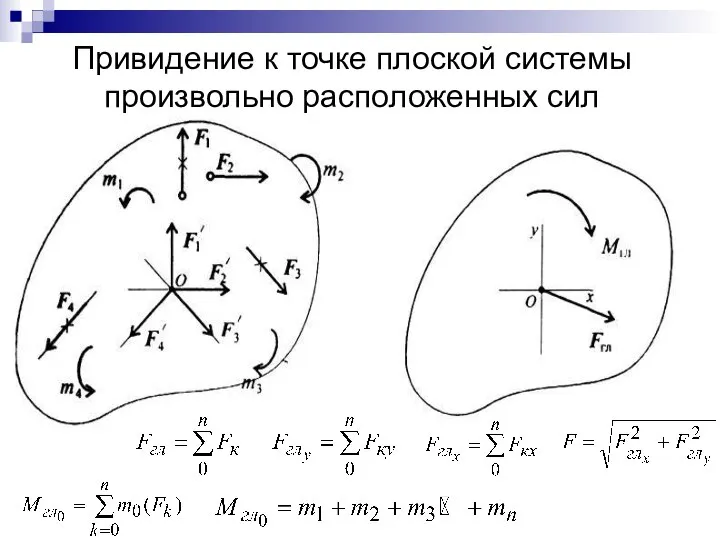
- 28. Привидение к точке плоской системы произвольно расположенных сил
- 29. Точку приложения равнодействующей можно определить по формуле где d – расстояние от выбранной точки приведения до
- 31. Основная форма уравнения равновесия:
- 32. Теорема Вариньона о моменте равнодействующей произвольной плоской системы сил
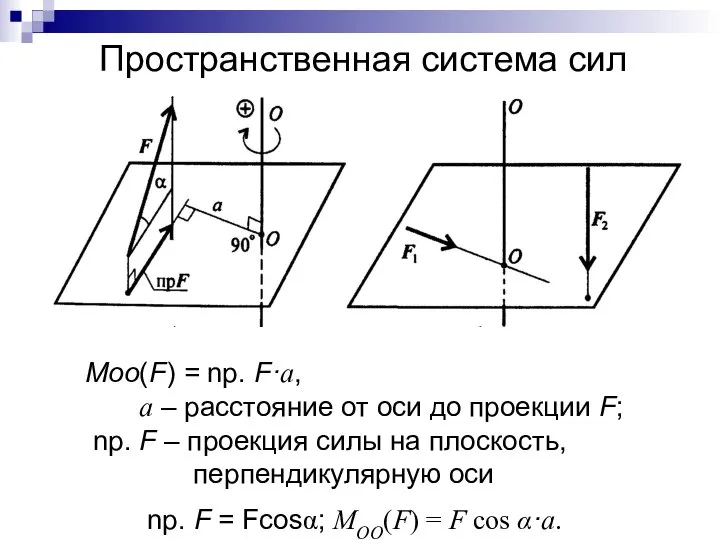
- 33. Пространственная система сил Moo(F) = np. F·a, a – расстояние от оси до проекции F; np.
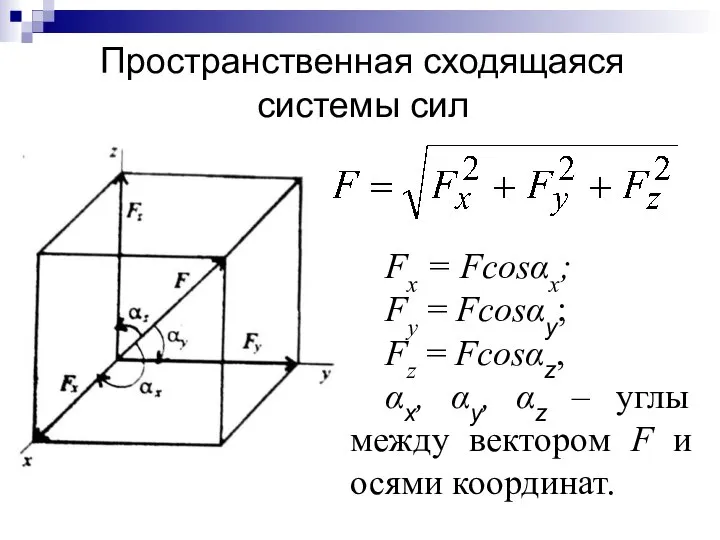
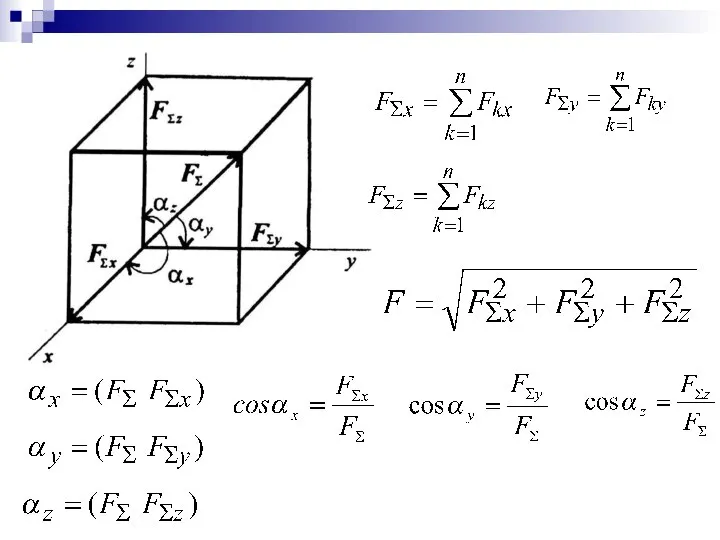
- 34. Пространственная сходящаяся системы сил Fx = Fcosαx; Fy = Fcosαy; Fz = Fcosαz, αx, αy, αz
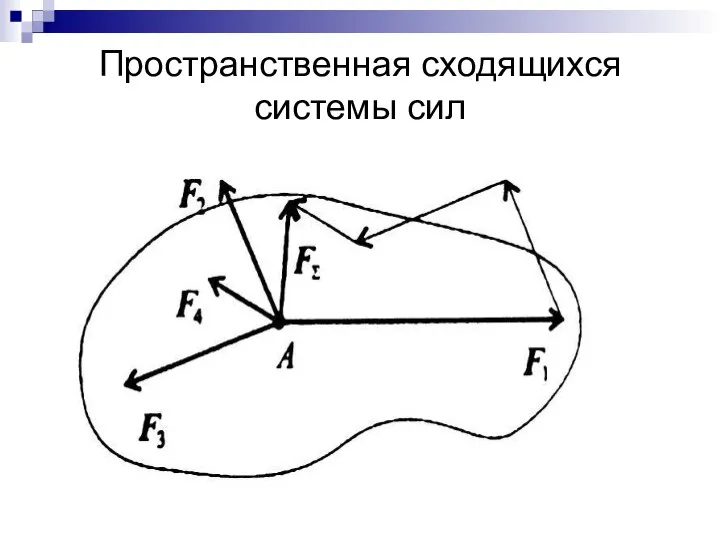
- 35. Пространственная сходящихся системы сил
- 36. .
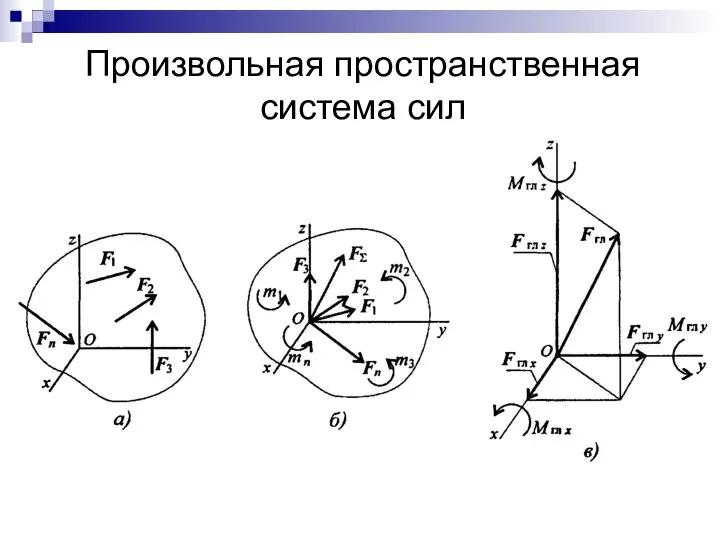
- 37. Произвольная пространственная система сил
- 39. Уравнения равновесия пространственной системы сил
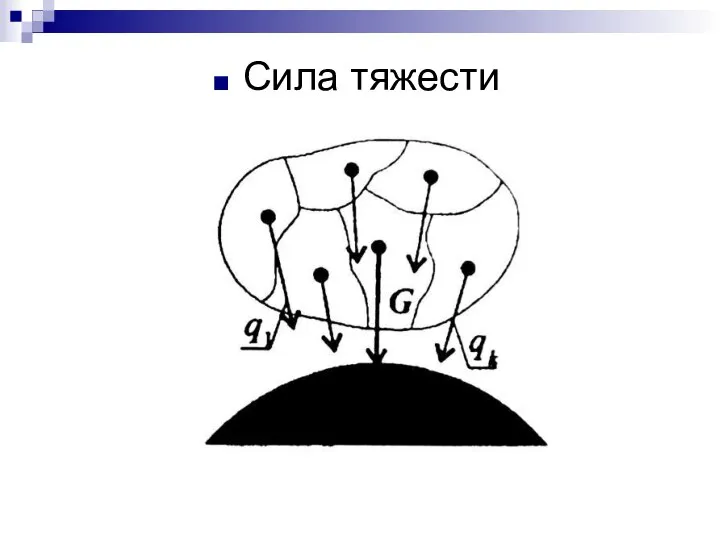
- 40. Сила тяжести
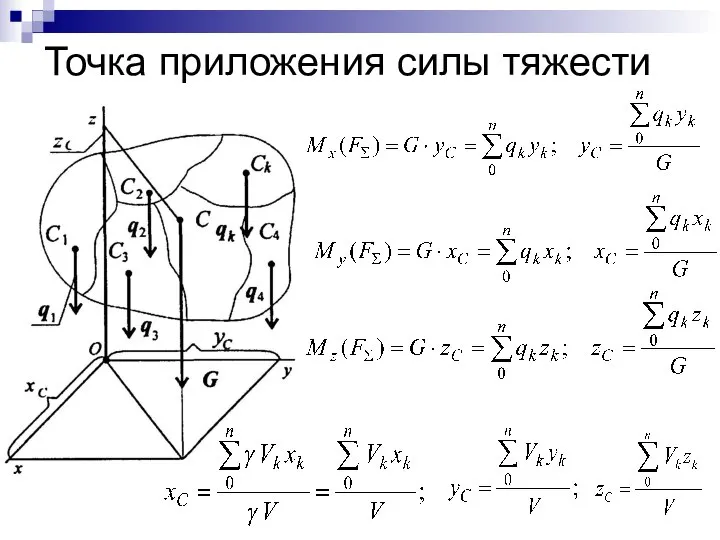
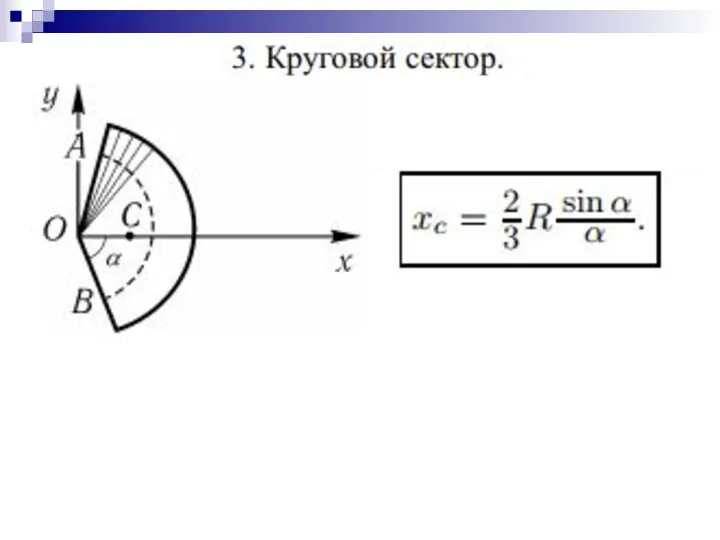
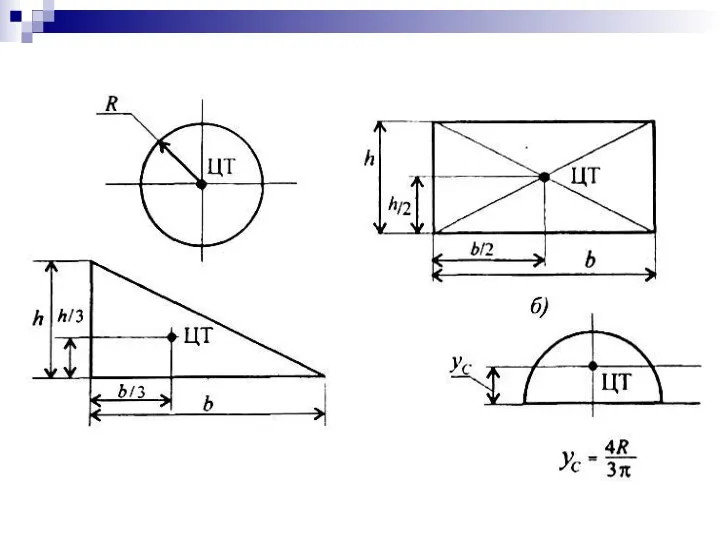
- 41. Точка приложения силы тяжести
- 42. Для плоских тел: V = Ah, где А – площадь фигуры, h – ее высота Определение
- 46. При решении задач используются следующие методы: 1) Аналитический (интегрированием)
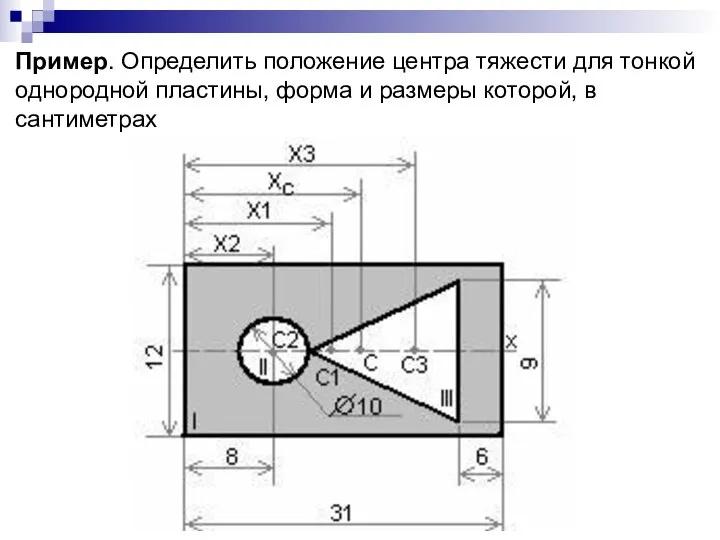
- 47. Пример. Определить положение центра тяжести для тонкой однородной пластины, форма и размеры которой, в сантиметрах
- 48. Решение. Данную фигуру представляем состоящей из трех простых фигур: 1 – прямоугольник, 2 – круга, 3
- 49. Координаты центра тяжести простых фигур: х1=31/2=15,5 см, х2=8см, х3=31-6-12/3=21см, где 12/3 – расстояние от центра тяжести
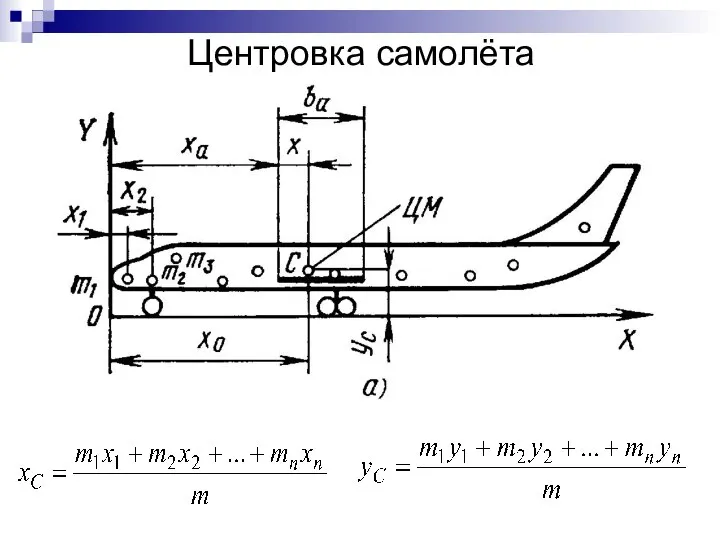
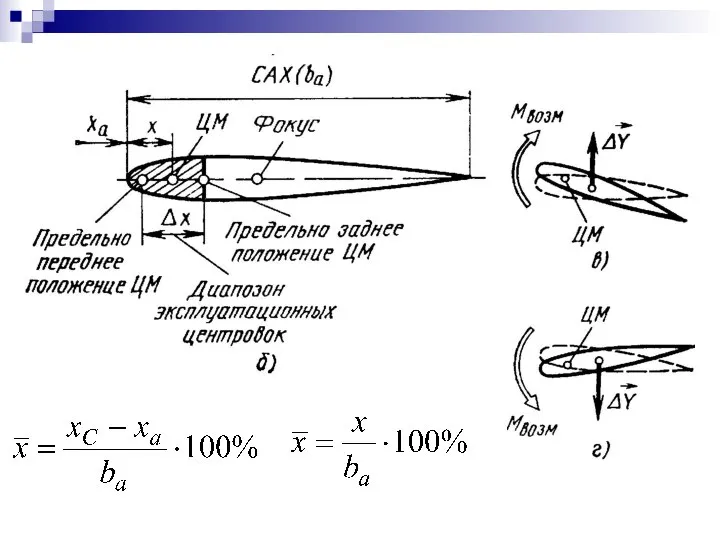
- 50. Центровка самолёта
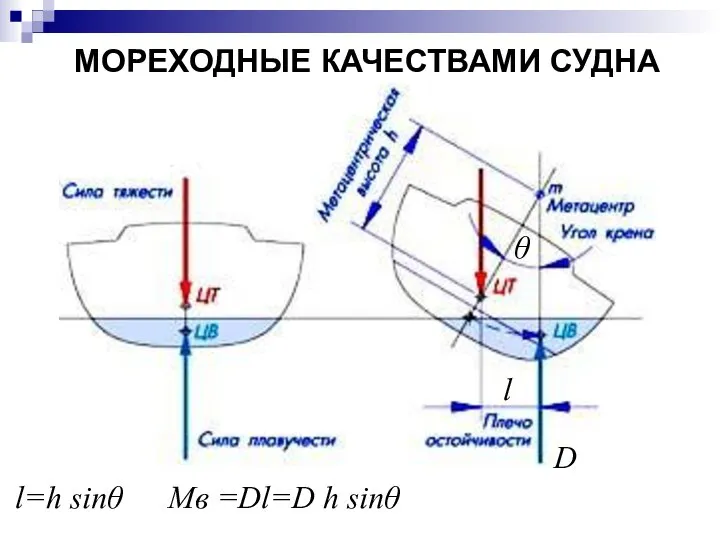
- 52. МОРЕХОДНЫЕ КАЧЕСТВАМИ СУДНА l θ l=h sinθ Mв =Dl=D h sinθ D
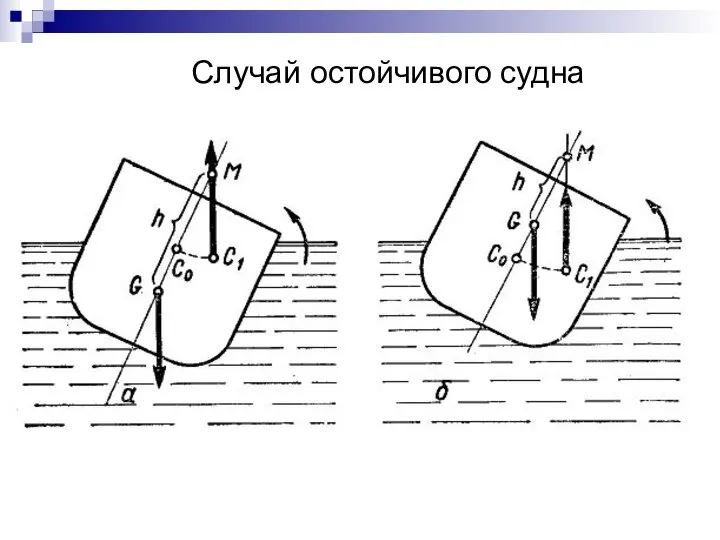
- 54. Случай остойчивого судна
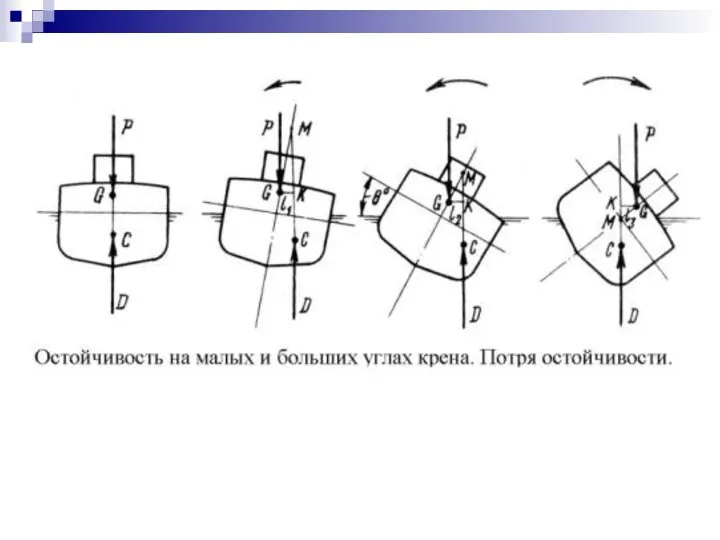
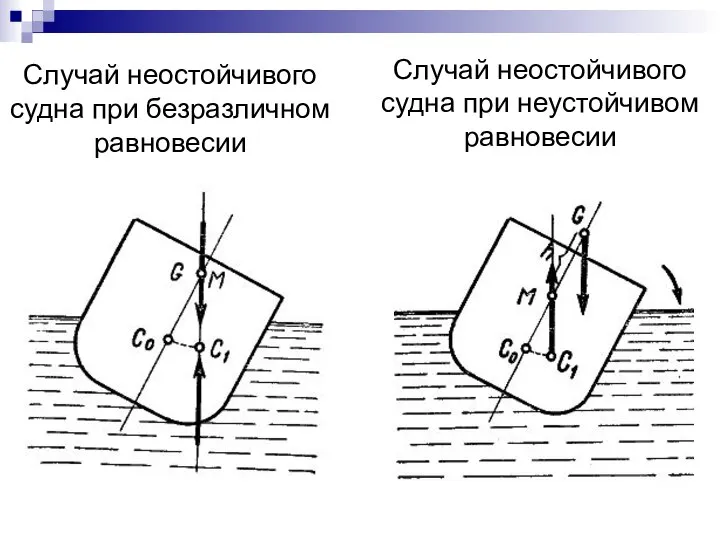
- 55. Случай неостойчивого судна при безразличном равновесии Случай неостойчивого судна при неустойчивом равновесии
- 56. Для классической яхты “Contessa 32” потеря остойчивости наступает только при крене 155°
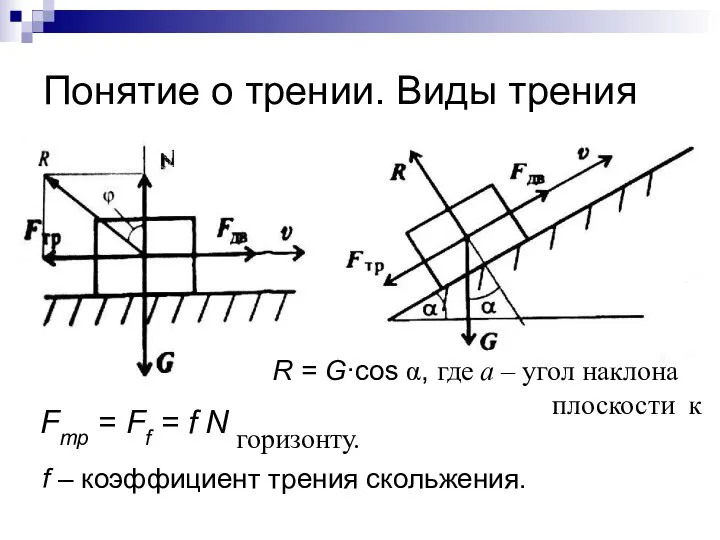
- 57. Понятие о трении. Виды трения Fтр = Ff = f N, f – коэффициент трения скольжения.
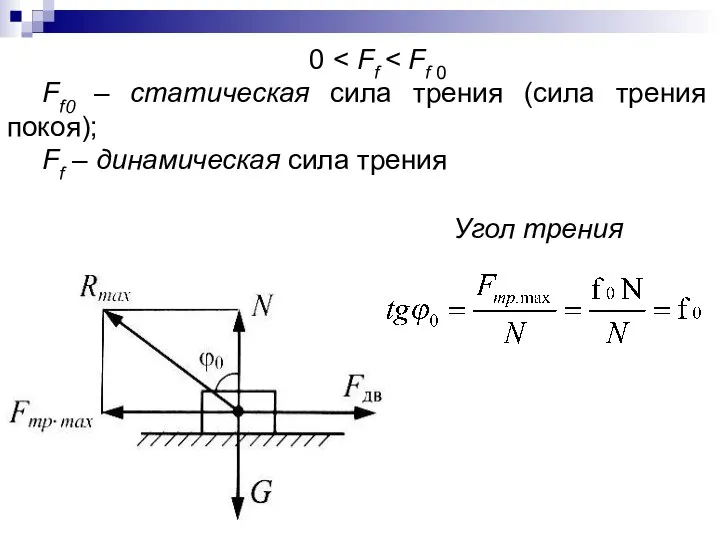
- 58. 0 Ff 0 – статическая сила трения (сила трения покоя); Ff – динамическая сила трения Угол
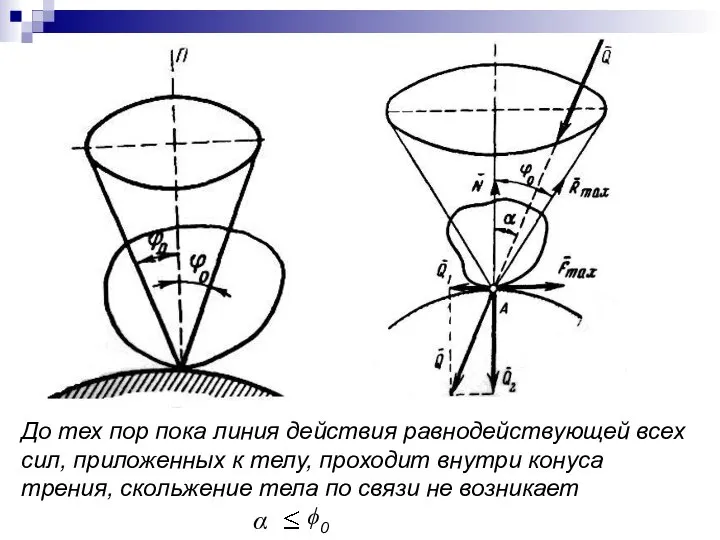
- 59. . До тех пор пока линия действия равнодействующей всех сил, приложенных к телу, проходит внутри конуса
- 61. Скачать презентацию


















 Момент силы
Момент силы 21 061
21 061 Крылья России
Крылья России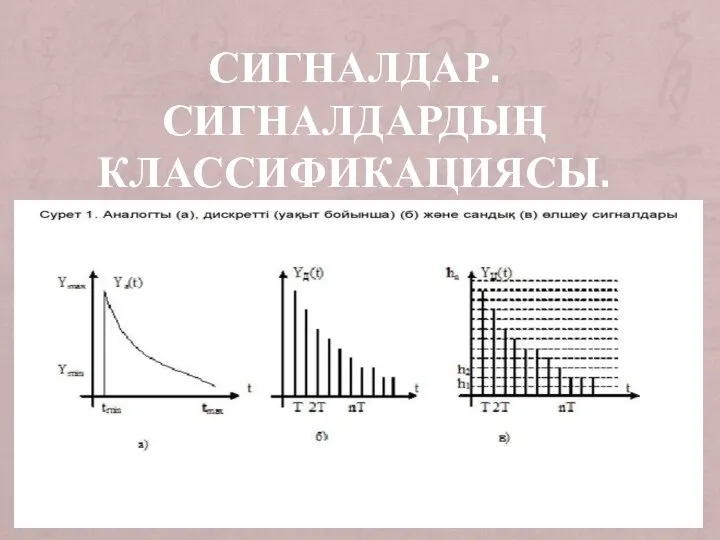 Сигналдар. Сигналдардың классификациясы
Сигналдар. Сигналдардың классификациясы Неравновесные состояния и необратимые процессы. Броуновское движение
Неравновесные состояния и необратимые процессы. Броуновское движение 1435976
1435976 Спектроскопия упруго-рассеянных электронов на отражение
Спектроскопия упруго-рассеянных электронов на отражение Релятивистский закон сложения скоростей
Релятивистский закон сложения скоростей Электромагнитные индукции
Электромагнитные индукции Прозрачный люминесцентный солнечный концентратор
Прозрачный люминесцентный солнечный концентратор Назначение основных размеров опор и определение нагрузок, действующих на опоры
Назначение основных размеров опор и определение нагрузок, действующих на опоры Трансмиссия автомобиля
Трансмиссия автомобиля Презентация на тему Свет. Прямолинейное распространение света
Презентация на тему Свет. Прямолинейное распространение света  Типы соединений потребителей тока
Типы соединений потребителей тока Решение задач на тепловые процессы
Решение задач на тепловые процессы Презентация на тему Создание вечного двигателя
Презентация на тему Создание вечного двигателя  Lektsia_2
Lektsia_2 Презентация по физике "Механика.Система отсчета.Путь и перемещение.Средняя скорость" -
Презентация по физике "Механика.Система отсчета.Путь и перемещение.Средняя скорость" -  Общее по электрическим машинам
Общее по электрическим машинам Способы изготовление байдарки
Способы изготовление байдарки Электромагнитная индукция
Электромагнитная индукция Теоретическая механика. Кинематика. (Часть 2)
Теоретическая механика. Кинематика. (Часть 2) Мир без денег – это возможно?
Мир без денег – это возможно? Работа совершаемая при термодинамических процессах. Количество теплоты. Теплоемкость
Работа совершаемая при термодинамических процессах. Количество теплоты. Теплоемкость Решение задач репетиционного тестирования по физике, этап 1
Решение задач репетиционного тестирования по физике, этап 1 Закон сохранения импульса
Закон сохранения импульса Напряженность электростатического поля
Напряженность электростатического поля Закон сохранения энергии
Закон сохранения энергии