Определение кинематических параметров движения

Расчетные формулы для определения параметров движения
Движение точки, поступательное движение тела:
1)Равномерное движение
аt =0 , v = const
S=v∙t, ( а = aп = при криволинейном движении)
2) Неравномерное движение
S = f (t) , (где t3 и степень выше, скорость и ускорение
определяются через производные)
V = S′ , at = V′ = S″ ,
Полное ускорение:
3) Равнопеременное движение
v ≠ const. аt = const аt > 0 -равноускоренное
аt < 0 - равнозамедленное

Параметры вращательного движения:
φ — угол поворота тела, угловое перемещение φ = f(t), [φ] = рад;
Один полный оборот: 2π, тогда число оборотов тела можно определить:
2) ω — угловая скорость, [ω] = рад/с, в общем случае определяется:
ω = φ‘ –угловая скорость есть первая производная от углового перемещения по времени.
Еще одна характеристика скорости вращения - частота вращения п, измеряется в оборотах в минуту, [об/мин]
Угловая скорость и частота вращения связаны зависимостью:
3) Угловое ускорение ε, [ε] = рад/с2, в общем случае определяется
ε = ω' = φ'' – первая производная угловой скорости или вторая производная углового перемещения.

Виды вращательного движения
1) Равномерное вращение (угловая скорость постоянна):
ω = const.
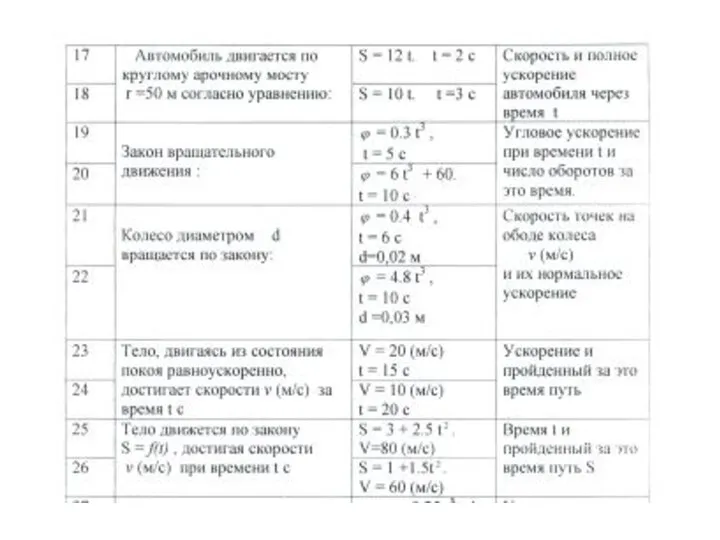
Уравнение (закон) равномерного вращения в данном случае имеет вид:
φ = ωt.
2) Неравномерное вращение , когда φ = f(t), ( t в третьей степени и выше).
Угловая скорость и угловое перемещение определяются через производные:
ω = φ‘ ; ε = ω' = φ''
3) Равнопеременное вращение (угловое ускорение постоянно):
ε = const.
- при ускоренном движении — ε > 0, угловая скорость будет все время возрастать.
- при замедленном движении — ε < 0, угловая скорость убывает.
где ω0 — начальная угловая скорость, рад/с
ω – угловая скорость в данный момент времени (конечная), рад/с
ε – угловое ускорение, рад/с2

Скорости и ускорения точек вращающегося тела
Тело вращается вокруг точки О.
Параметры движения точки А, расположенной на расстоянии r а от оси вращения (рис.).
Путь точки A: SA = φrА
Линейная скорость точки A: vA = ωrА
Ускорения точки A: atA = εrА — касательное;
апA = ω2 rА — нормальное,
где rА — радиус окружности, траектории точки А.

2.
Задача 1. Задача Задано уравнение движения точки S = 22t — 4t2 ,определить скорость и касательное ускорение в начале движения и касательное ускорение конце 5 секунды движения.
Задача 2. Тело вращалось равноускорено из состояния покоя и сделало 360 оборотов за 2 мин. Определить угловое ускорение.
Решение
_______

Задача 3. Маховое колесо вращается равномерно со скоростью 120 об/мин (рис. ). Радиус колеса 0,3 м. Определить скорость и полное ускорение точек на ободе колеса
Решение:
vA = ωrА
Угловая скорость
Касательное ускорение точки A atA = 0, т.к. atA = εrА , а ε=0 - равномерное вращение;
Нормальное ускорение точки А аnA = ω2rA
апA = (12,56)2 • 0,3 = 47,3м/с2.
Полное ускорение точек на ободе колеса:
______
______

3. Отчет .Задача