Слайд 4К выводу основного уравнения статики атмосферы
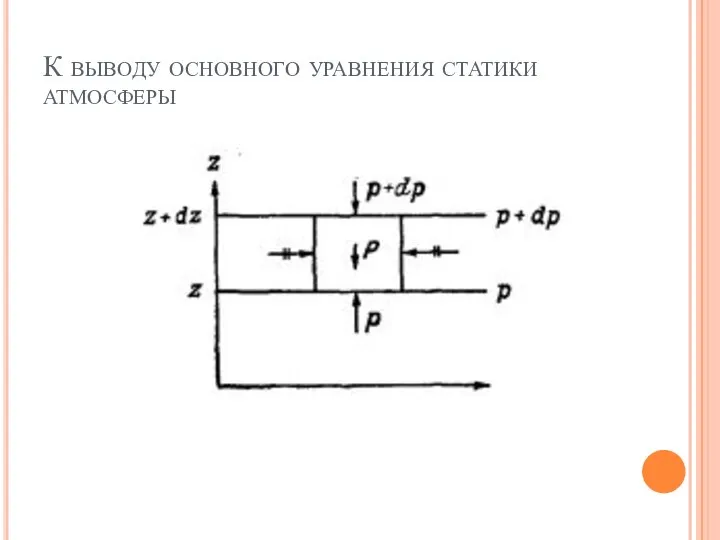
Слайд 6Сумма проекций сил, действующий на выделенный объем воздуха
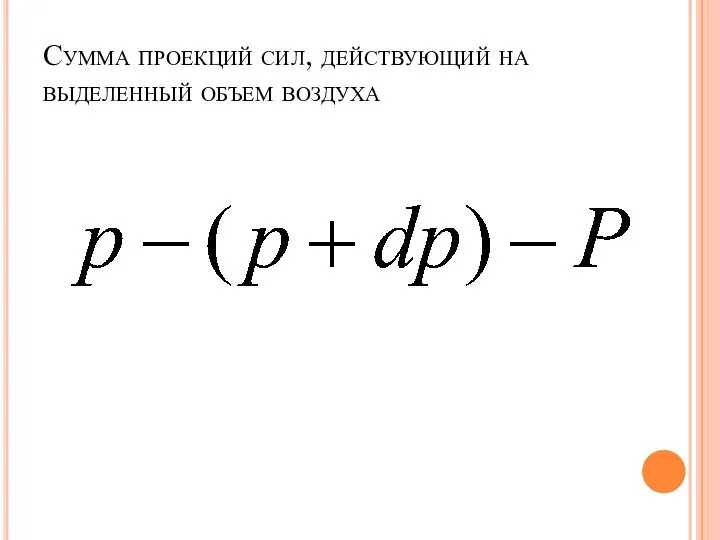
Слайд 9Основное уравнение статики атмосферы выражает условия равновесия двух сил: вертикального градиента давления

и силы тяжести
Слайд 11Выводы из основного уравнения статики
Вывод №1.
Если dz>0, то dp<0
В атмосфере давление всегда

убывает с увеличением высоты
Слайд 12Вывод №2.
Вес вертикального столба воздуха
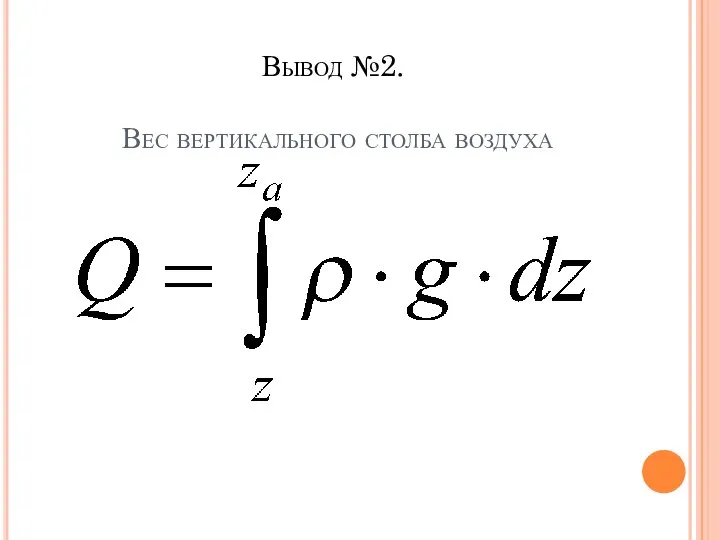
Слайд 13Вывод №2. атмосферное давление или давление воздуха, на каждом уровне равно весу
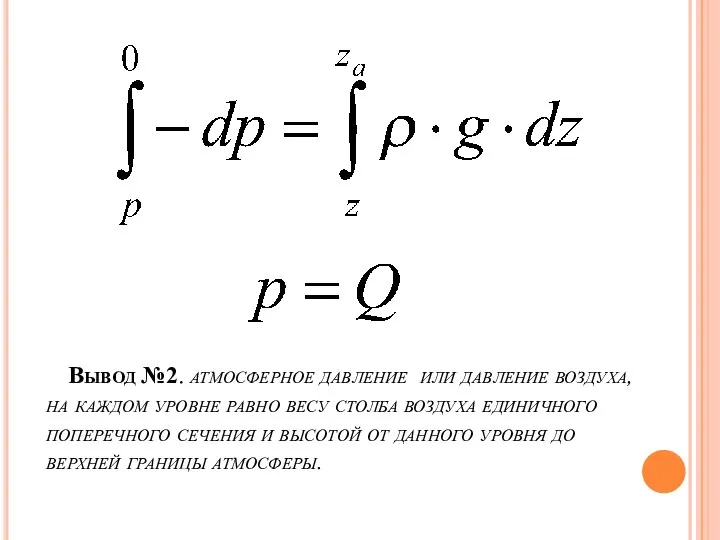
столба воздуха единичного поперечного сечения и высотой от данного уровня до верхней границы атмосферы.
Слайд 14Вывод №3.
При увеличении высоты на одно и то же значение относительно

некоторой изобарической поверхности понижение давления в более холодной воздушной массе больше, чем в теплой массе, т.е. в холодной массе давление убывает с высотой быстрее, чем в более теплой воздушной массе.
Слайд 16Интегралы основного уравнения статики, полученные при различных предположениях относительно изменения температуры и

плотности воздуха с высотой называются барометрическими формулами.
Слайд 19Уравнение состояния влажного воздуха:
P = ρRсTв
где виртуальная температура:
Tв = T(1+0,608s)

Слайд 25Величина обратная барической ступени, вертикальный барический градиент – падение давления на единицу

прироста высоты: – (dp/ dz), единица измерения гПа/100 м.
Всю атмосферу можно представить пронизанной системой изобарических поверхностей, огибающих земной шар. Эти поверхности пересекаются с уровнями под очень малыми углами.
Слайд 26Высота расположения изобарических поверхностей:
1000 гПа – над уровнем моря,
700 гПа –

3 км,
500 гПа – 5 км,
300 гПа – 9 км,
200 гПа – 12 км,
100 гПа – 16 км,
50 гПа – 20 км.
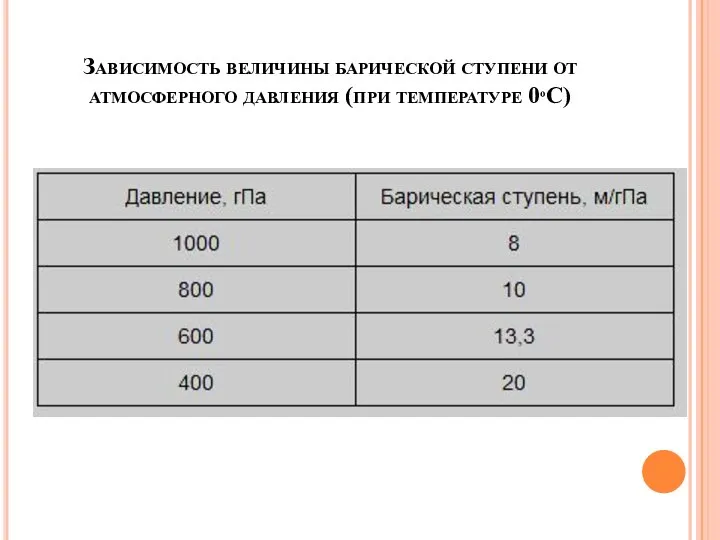
Слайд 27Зависимость величины барической ступени от атмосферного давления (при температуре 0ºС)
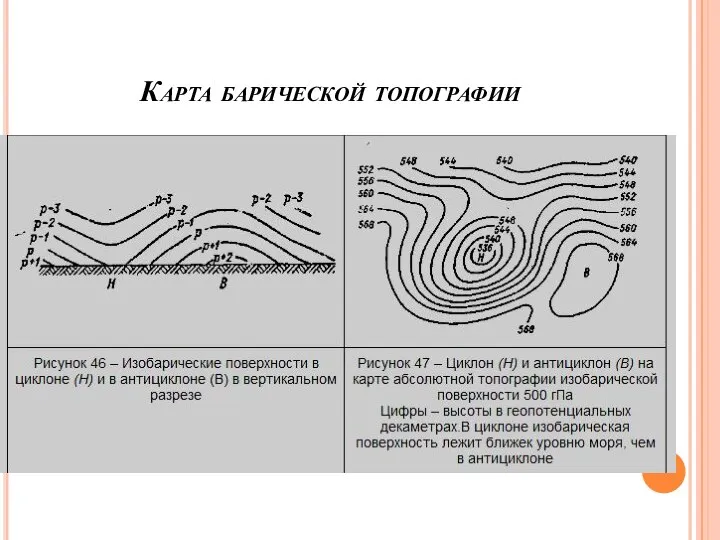
Слайд 28На практике для изображения распределения давления на высоте пользуются картами барической топографии

(барического рельефа), показывающими положение в пространстве той или иной изобарической поверхности.
Карта барической топографии - это карта, на которую нанесены высоты или геопотенциалы той или иной изобарической поверхности над уровнем моря (карта абсолютной барической топографии) или над уровнем нижележащей изобарической поверхности (карта относительной барической топографии).
На карты барической топографии иногда наносят и другие элементы: температуру и ветер на данной поверхности, термический ветер для слоя между двумя изобарическими поверхностями (карты относительной барической топографии).
Слайд 30С помощью барометрической формулы можно решать три задачи:
1) приведение давления одного уровня

к другому (известны давление на одном уровне и перепад высот, средняя температура слоя, найти давление на другом уровне)
2) барометрическое нивелирование (известны давление на двух уровнях, средняя температура столба воздуха, найти перепад высот)
3) определение средней температуры слоя (известны давление на двух уровнях и перепад высот, найти среднюю температуру слоя).
Слайд 33Барометрические формулы при постоянной плотности (однородная атмосфера)

Слайд 35Барометрические формулы при постоянной температуре (изотермическая атмосфера)

Слайд 36Барометрические формулы при постоянном температурном градиенте (политропная атмосфера)

Слайд 37Барометрические формулы при произвольном изменении температуры с высотой (общий случай)

Слайд 38для любого распределения температуры воздуха по высоте

Слайд 391. Если γ > γА= 3,42 oС/100 м, то dρ/dz > 0,

т. е. плотность воздуха возрастает с высотой. Вертикальные градиенты температуры γ, превышающие 3,42 oС/100 м, в реальных условиях атмосферы могут наблюдаться лишь в дневные часы (летом) в приземном слое атмосферы. При таких условиях плотность в этом слое увеличивается с высотой.
2. Если γ = γА, то dρ/dz = 0, т. е. плотность воздуха не изменяется с высотой (постоянна): ρ = ρ0 = const. Это случай однородной атмосферы.
3. Если γ < γА, то dρ/dz < 0, т. е. плотность воздуха убывает с высотой. Этот случай является абсолютно преобладающим в условиях атмосферы.
Слайд 40Полная барометрическая формула (формула Лапласа)
C1 = 0,0036 (1/град)
C2 = 0,378
C3 =

0,00264
C4 = 3,14·10^(-7) м
Слайд 41сокращенная барометрическая формула (для реальной атмосферы)

Слайд 43Средняя арифметическая температура
Барометрическая формула (при z1=0, z2=z):

Слайд 44Геопотенциал – потенциальная энергия единицы массы Ф в поле силы тяжести:
dФ =g

dz.
Единицей измерения геопотенциала служит геопотенциальный (гп) метр, который численно близок к обычному метру.
Слайд 45Абсолютной высотой (абсолютным геопотенциалом) изобарической поверхности называют геопотенциальную высоту изобарической поверхности над

уровнем моря.
Слайд 46Приращение абсолютного геопотенциала

Слайд 47Относительной высотой одной изобарической поверхности над другой (относительным геопотенциалом) называется толщина слоя

в геопотенциальных метрах между этими изобарическими поверхностями (разность их абсолютных геопотенциалов).
Слайд 49Изобара – линия, соединяющие точки с равным атмосферным давлением.
Изобары можно проводить через

2, 5, 10 гПа.
Горизонтальный барический градиент – изменение давления на единицу расстояния в горизонтальной плоскости (на поверхности уровня). Модуль горизонтального барического градиента обратно пропорционален расстоянию между изобарами.
Слайд 50Вектор горизонтального барического градиента обычно обозначают – р.
– (Δр/Δn),
где Δр

– разность давления между двумя изобарами,
Δn – расстояние между ними.
Единицы измерения гПа/100км или гПа/111 км (1º долготы).
Слайд 51Области повышенного или пониженного давления, на которые расчленяется барическое поле атмосферы называются

барическими системами.
Основные типы барических систем:
А) с замкнутыми изобарами:
1) циклон,
2) антициклон;
Б) с незамкнутыми изобарами:
1) ложбина,
2) гребень,
3) седловина.
Слайд 52Изобары на уровне моря в различных типах барических систем:
I – циклон, II
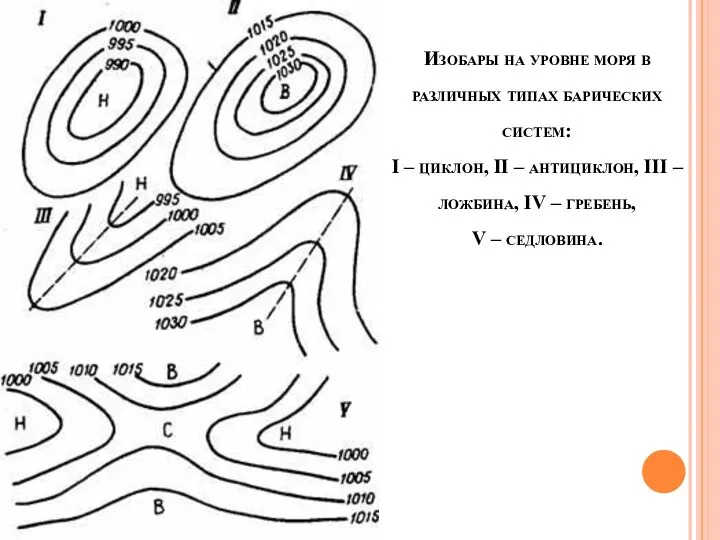
– антициклон, III – ложбина, IV – гребень,
V – седловина.
Слайд 53Основные типы барических систем:
Антициклон – область повышенного атмосферного давления с замкнутыми концентрическими

изобарами на уровне моря и соответствующим распределением ветров (в Северном полушарии – по часовой стрелке). Горизонтальный барический градиент направлен от центра к периферии.
Ложбина – полоса пониженного давления между двумя областями повышенного давления. Изобары либо почти параллельные, либо имеют вид латинской буквы V. Центра в ложбине нет, есть ось (линия на которой атмосферное давление имеет минимальное значение, или на которой изобары резко меняют направление простирания).


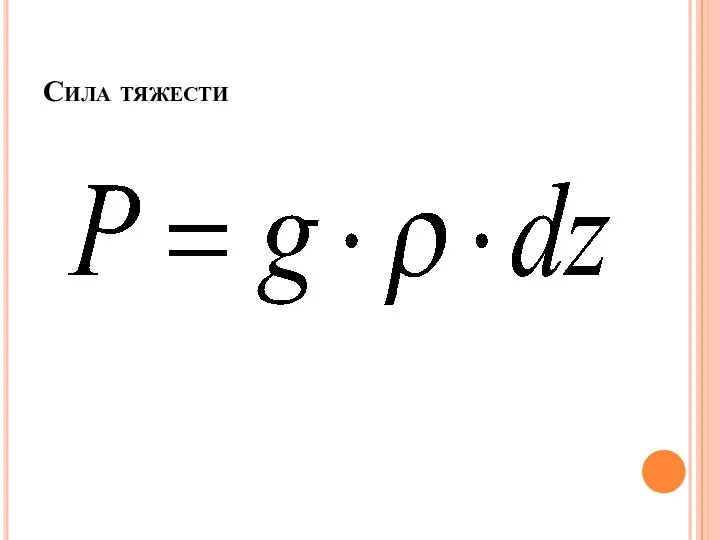
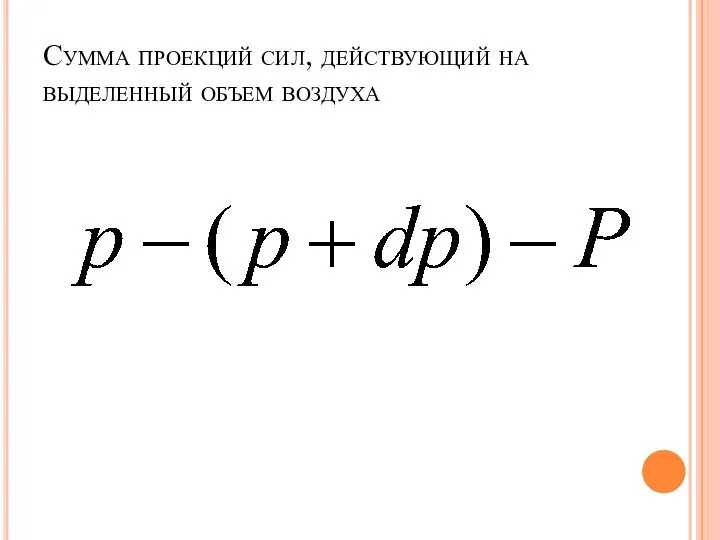
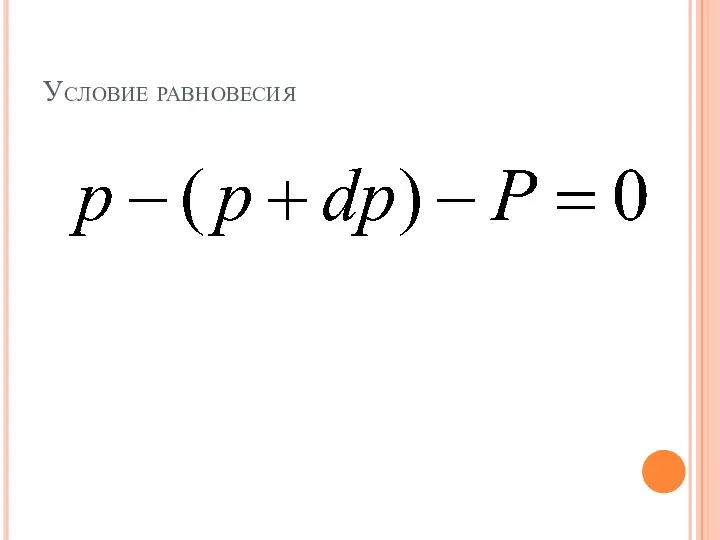
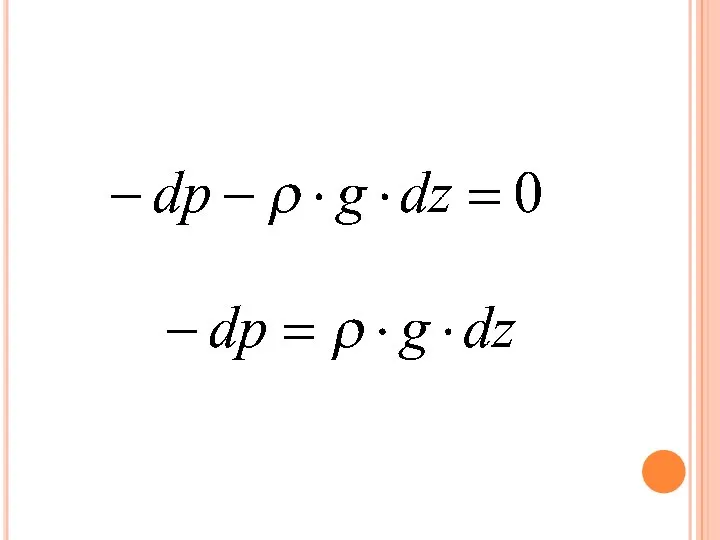

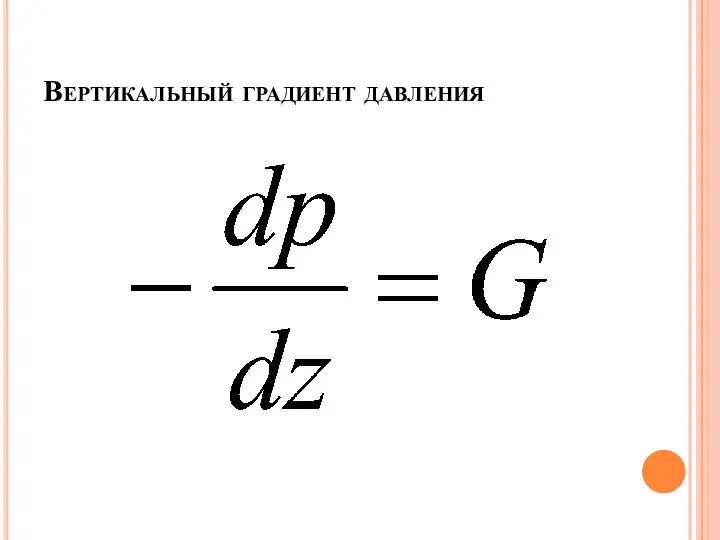

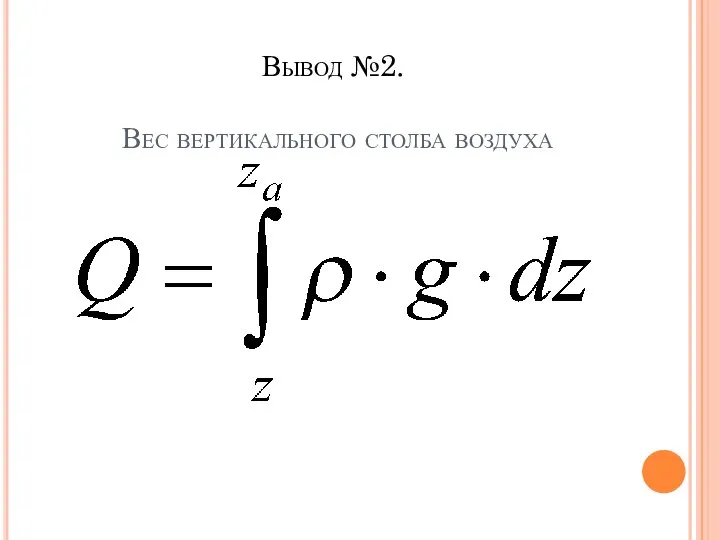
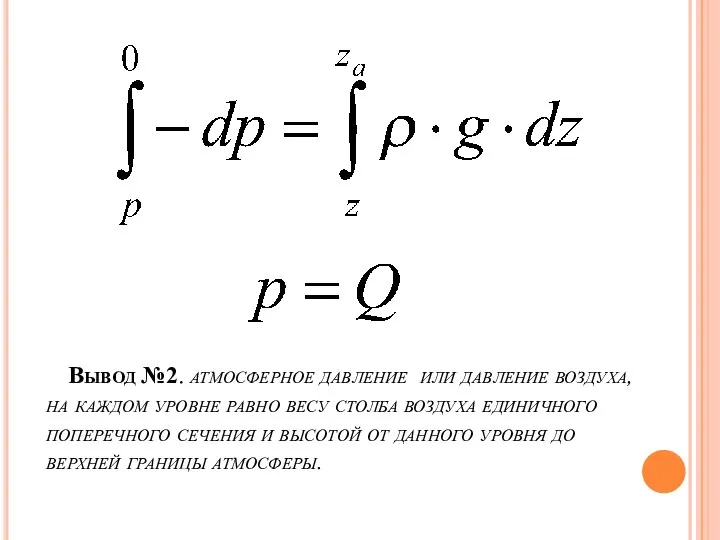



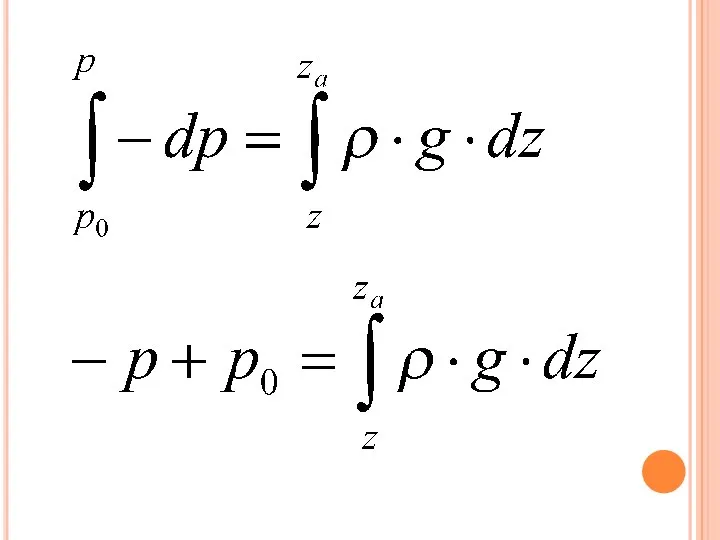
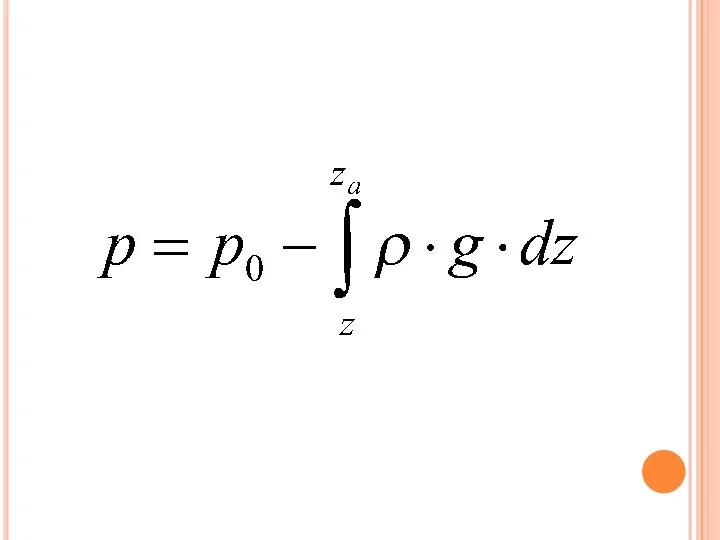

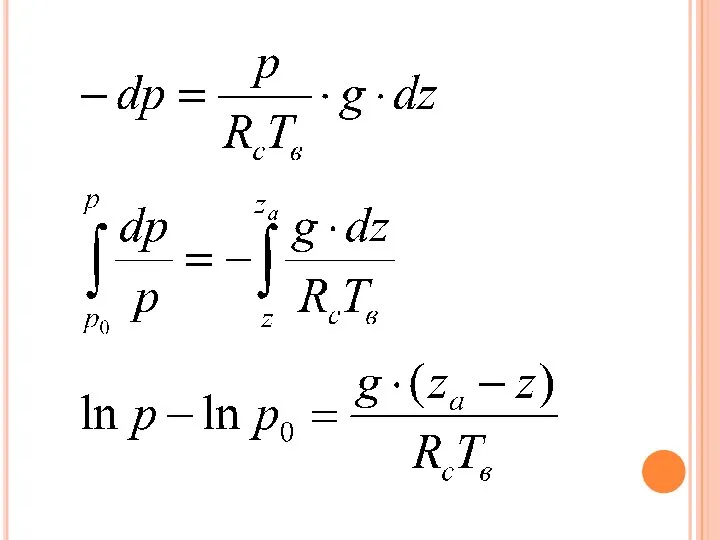
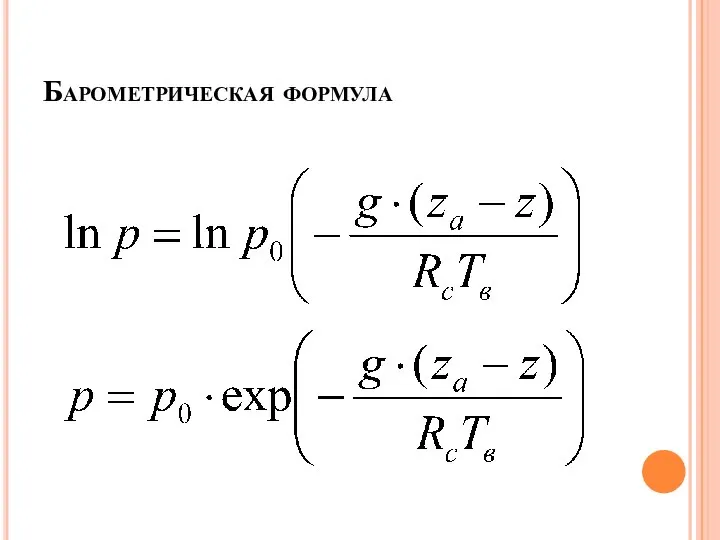































 Относительность движения. Инерциальные системы отсчета. Первый закон Ньютона
Относительность движения. Инерциальные системы отсчета. Первый закон Ньютона Колебания и волны. Волновая оптика
Колебания и волны. Волновая оптика Электрический ток и его применение
Электрический ток и его применение Физические величины. Измерение физических величин. Точность и погрешность измерений
Физические величины. Измерение физических величин. Точность и погрешность измерений Относительность движения
Относительность движения Урок 05 Сила Ампера
Урок 05 Сила Ампера Презентация на тему Эмилий Ленц
Презентация на тему Эмилий Ленц  Необычные барометры
Необычные барометры Курс физики.Основы квантовой физики. Часть 2
Курс физики.Основы квантовой физики. Часть 2 Подготовка машины к работе
Подготовка машины к работе Презентация на тему Использование информационных технологий в преподавании физики
Презентация на тему Использование информационных технологий в преподавании физики  Постоянный электрический ток
Постоянный электрический ток Электроэнергия Ксенон (Светодиоды)
Электроэнергия Ксенон (Светодиоды) Сила. Динамометр
Сила. Динамометр 4. Механика твердого тела
4. Механика твердого тела Тепловое расширение
Тепловое расширение Презентация на тему Возможно ли создать электричество дома
Презентация на тему Возможно ли создать электричество дома  Гидростатическое давление
Гидростатическое давление Структурные методы анализа
Структурные методы анализа Презентация на тему Теория вечной Вселенной и Большого взрыва
Презентация на тему Теория вечной Вселенной и Большого взрыва  Температура.. Внутренняя энергия
Температура.. Внутренняя энергия Полупроводники. Собственная проводимость полупроводников
Полупроводники. Собственная проводимость полупроводников Теоретическая механика. Дифференциальные уравнения движения. Криволинейное движение (задачи)
Теоретическая механика. Дифференциальные уравнения движения. Криволинейное движение (задачи) Приготовьтесь к построению! Урок физики
Приготовьтесь к построению! Урок физики Способы соединения частей: шестеренки
Способы соединения частей: шестеренки Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии в колебательных системах
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии в колебательных системах Л2 мех.оборуд
Л2 мех.оборуд Путешествие по океану Знаний
Путешествие по океану Знаний