Содержание
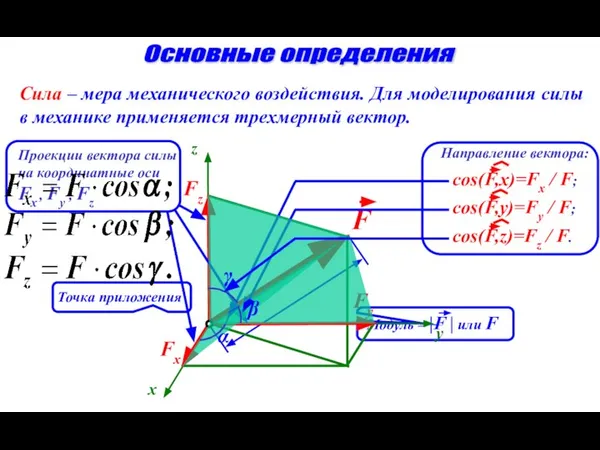
- 2. Основные определения Сила – мера механического воздействия. Для моделирования силы в механике применяется трехмерный вектор. x
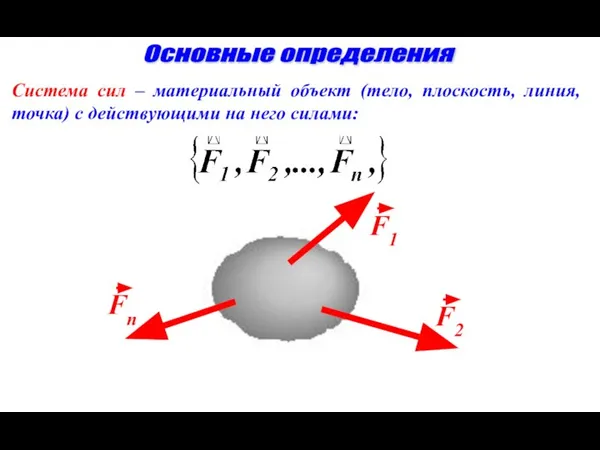
- 3. Основные определения Система сил – материальный объект (тело, плоскость, линия, точка) с действующими на него силами:
- 4. Основные определения Эквивалентные системы сил – системы, придающие механическому объекту одинаковое изменение движения:
- 5. Основные определения Уравновешенная (эквивалентная нулю) система сил – система сил, которая будучи добавлена или изъята из
- 6. Основные определения
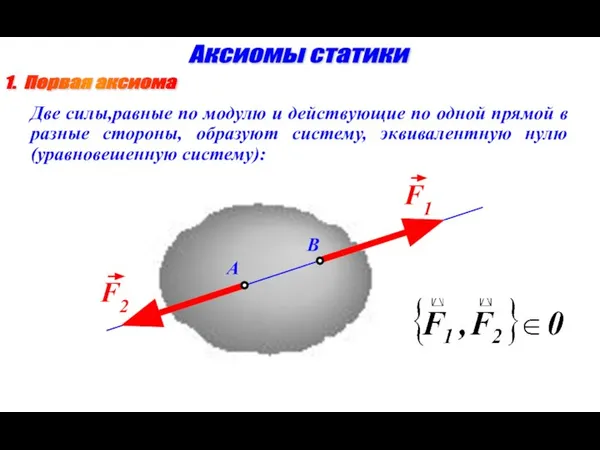
- 7. 1. Первая аксиома Аксиомы статики Две силы,равные по модулю и действующие по одной прямой в разные
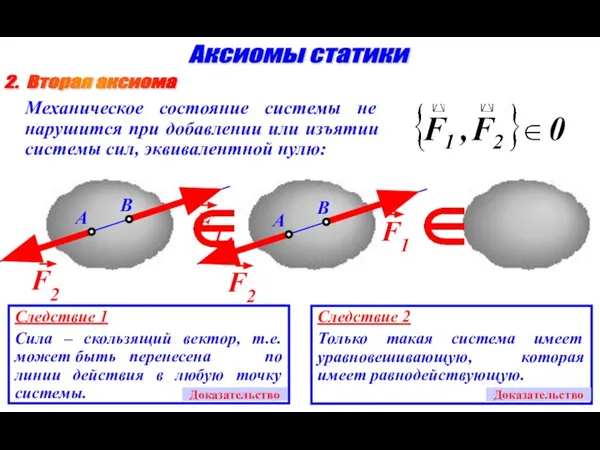
- 8. Аксиомы статики 2. Вторая аксиома Механическое состояние системы не нарушится при добавлении или изъятии системы сил,
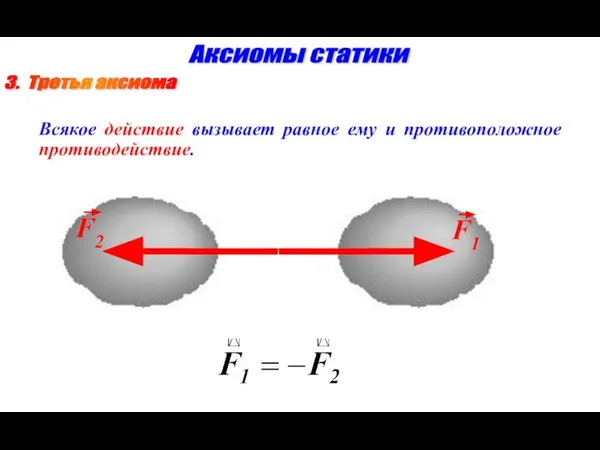
- 9. 3. Третья аксиома Аксиомы статики Всякое действие вызывает равное ему и противоположное противодействие.
- 10. Аксиомы статики 4. Четвертая аксиома Система из двух сил, приложенных в одной точке всегда имеет равнодействующую.
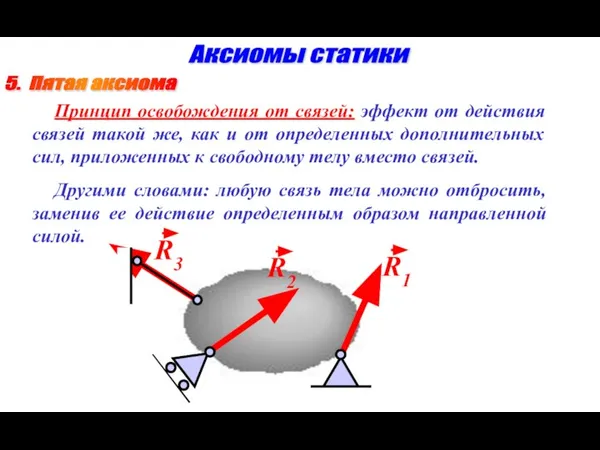
- 11. 5. Пятая аксиома Аксиомы статики Принцип освобождения от связей: эффект от действия связей такой же, как
- 12. Аксиомы статики 6. Шестая аксиома Аксиома отвердевания: Равновесие системы не нарушится при наложении дополнительных связей. В
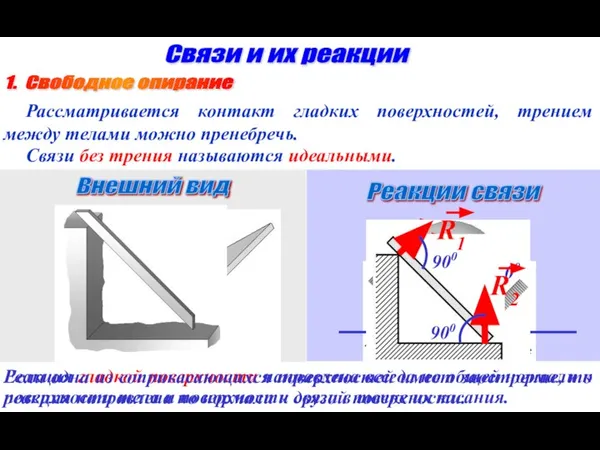
- 13. 1. Свободное опирание Рассматривается контакт гладких поверхностей, трением между телами можно пренебречь. Связи без трения называются
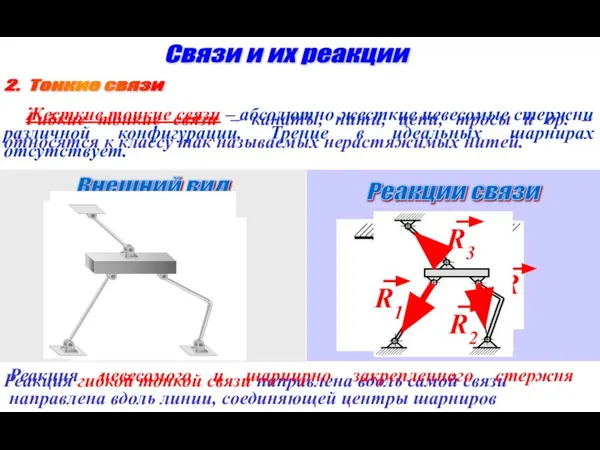
- 14. Внешний вид Реакции связи 2. Тонкие связи Связи и их реакции Гибкие тонкие связи – канаты,
- 15. Внешний вид Реакции связи Связи и их реакции 3. Шарнирные связи 900 Подвижный цилиндрический шарнир. Тело
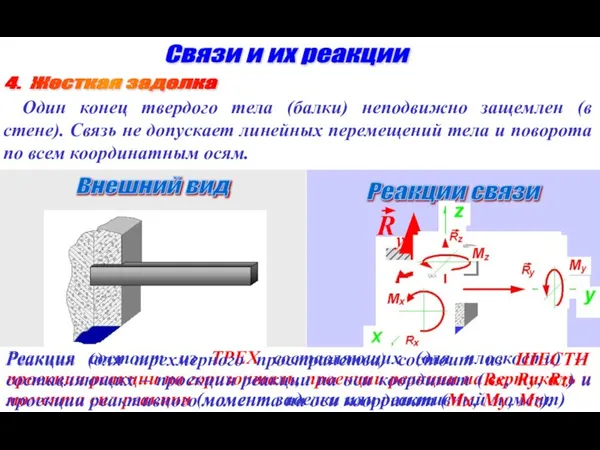
- 16. Связи и их реакции Внешний вид Реакции связи 4. Жесткая заделка Один конец твердого тела (балки)
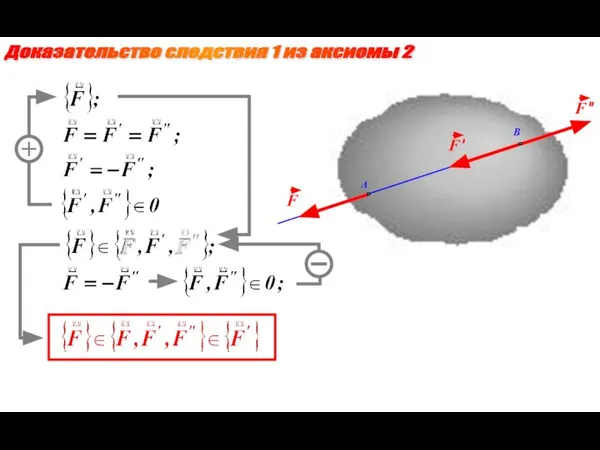
- 17. Доказательство следствия 1 из аксиомы 2 A B
- 19. Скачать презентацию





 Расчет направляющих. Анализ напряжений и деформаций направляющих в процессе работы ловителя
Расчет направляющих. Анализ напряжений и деформаций направляющих в процессе работы ловителя Занимательные опыты по физике
Занимательные опыты по физике Линзы. Оптика
Линзы. Оптика Заряды. Закон Кулона
Заряды. Закон Кулона Свердління отворів. Оброблення країв виробів
Свердління отворів. Оброблення країв виробів Il modello atomico di Schrödinger
Il modello atomico di Schrödinger Типовые соединения деталей машин
Типовые соединения деталей машин Вынужденные электромагнитные колебания
Вынужденные электромагнитные колебания Манометры
Манометры Решение задач репетиционного тестирования по физике, этап 1
Решение задач репетиционного тестирования по физике, этап 1 Основы аэродинамики
Основы аэродинамики sokhranenie_impulsa
sokhranenie_impulsa Лабораторные работы по курсу Математическое моделирование технических систем
Лабораторные работы по курсу Математическое моделирование технических систем Действие магнитного поля на проводник с током. Сила Ампера
Действие магнитного поля на проводник с током. Сила Ампера Курчатов Игорь Васильевич
Курчатов Игорь Васильевич Умная колонка на уроках физики
Умная колонка на уроках физики Обобщающий урок-соревнование по теме Электрические явления
Обобщающий урок-соревнование по теме Электрические явления Экспериментальные методы в радиофизике
Экспериментальные методы в радиофизике Электроэнергия. Гидроэлектростанция. Линия электропередач. Электролампа
Электроэнергия. Гидроэлектростанция. Линия электропередач. Электролампа Ядерные силы. Ядерные реакции
Ядерные силы. Ядерные реакции Классная физика. Квест-игра
Классная физика. Квест-игра Энергия системы неподвижных точечных зарядов
Энергия системы неподвижных точечных зарядов Презентация на тему Конвекция. Излучение
Презентация на тему Конвекция. Излучение  Популярные типы кузова автомобилей
Популярные типы кузова автомобилей Источники света. Распространение света
Источники света. Распространение света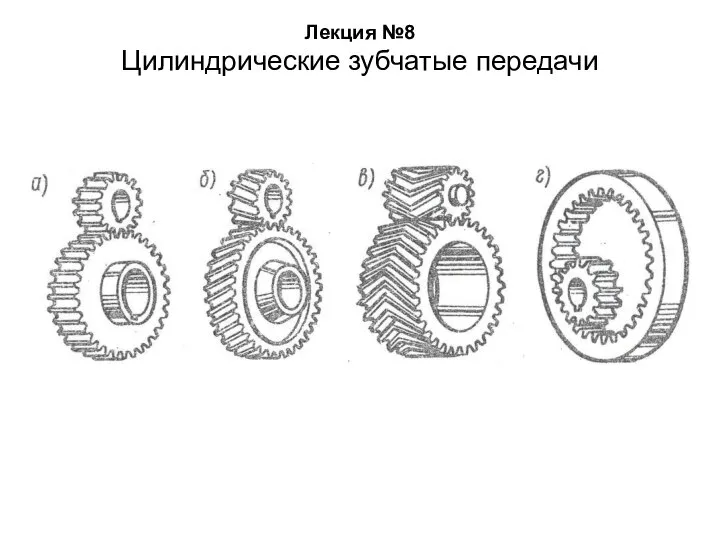 Цилиндрические зубчатые передачи. Лекции 8
Цилиндрические зубчатые передачи. Лекции 8 Разработкой технологии дефектации прибора системы зажигания автомобиля ГАЗ-2752 Газель
Разработкой технологии дефектации прибора системы зажигания автомобиля ГАЗ-2752 Газель Магнитное поле. Действие магнитного поля на проводник с током
Магнитное поле. Действие магнитного поля на проводник с током