Содержание
- 2. Национальный исследовательский ядерный университет «МИФИ» Задачи курса Знакомство с методами вычислительной математики, алгоритмами расчета и принципами
- 3. Национальный исследовательский ядерный университет «МИФИ» Программа курса Реализация на ЭВМ точных аналитических решений задач теплообмена Численное
- 4. Национальный исследовательский ядерный университет «МИФИ» Используемая литература Моделирование теплогидравлических процессов в реакторных установках и элементах теплообменного
- 5. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Применение: В качестве тестовых для
- 6. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Пример. Одномерное нестационарное поле температур
- 7. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Пример. Одномерное нестационарное поле температур
- 8. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Пример. Одномерное нестационарное поле температур
- 9. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Пример. Одномерное нестационарное поле температур
- 10. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Пример. Одномерное нестационарное поле температур
- 11. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Пример. Одномерное нестационарное поле температур
- 12. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений
- 13. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений
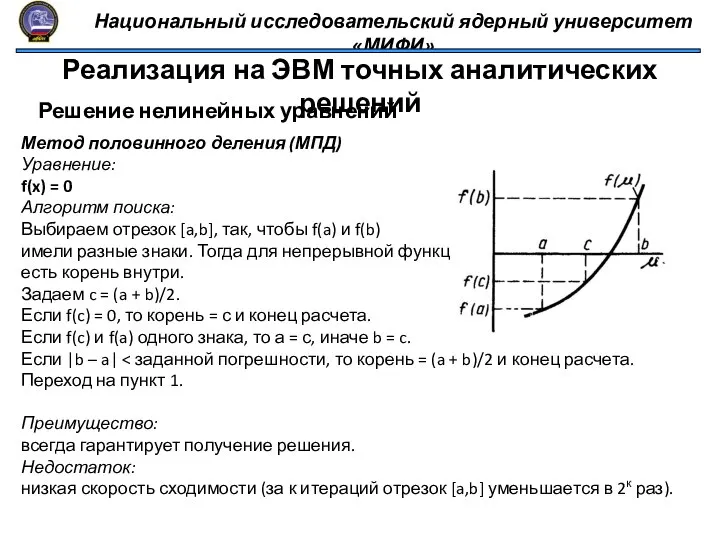
- 14. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений
- 15. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений
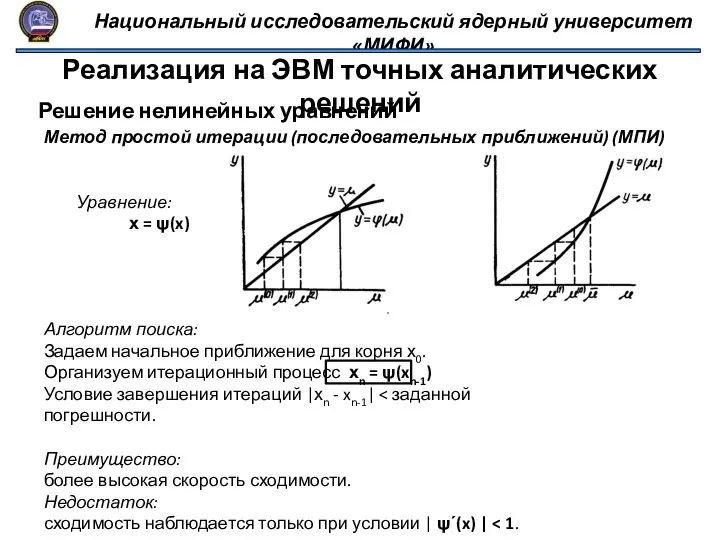
- 16. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений Метод простой
- 17. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений Усовершенствованный метод
- 18. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений Метод Ньютона-Рафсона
- 19. Национальный исследовательский ядерный университет «МИФИ» Реализация на ЭВМ точных аналитических решений Решение нелинейных уравнений Выбор вида
- 21. Скачать презентацию
















 Действие нескольких сил
Действие нескольких сил Движение и силы
Движение и силы Механические волны
Механические волны Проводники и диэлектрики в электростатическом поле
Проводники и диэлектрики в электростатическом поле Закон Ома, соединение проводников. Решение задач
Закон Ома, соединение проводников. Решение задач Итоговый тест на тему: Изменение агрегатных состояний вещества
Итоговый тест на тему: Изменение агрегатных состояний вещества Клепаные и сварные соединения
Клепаные и сварные соединения Марковские процессы
Марковские процессы Закон всемирного тяготения. Прямолинейное и криволинейное движение
Закон всемирного тяготения. Прямолинейное и криволинейное движение Механическое движение
Механическое движение Презентация на тему Механическая работа и мощность
Презентация на тему Механическая работа и мощность  graficheskoe_izobrazhenie_pryamolineynogo_ravnouskorennogo_dvizheniya
graficheskoe_izobrazhenie_pryamolineynogo_ravnouskorennogo_dvizheniya Визначення сталой в законі Стефана-Больцмана. Лабораторна робота № 50
Визначення сталой в законі Стефана-Больцмана. Лабораторна робота № 50 Терморезистор
Терморезистор Лабораторные работы по физике (10 класс)
Лабораторные работы по физике (10 класс) Электрический ток. Соединения проводников
Электрический ток. Соединения проводников Поле тяготения
Поле тяготения Давление. Задачи
Давление. Задачи Метод обращения движения
Метод обращения движения Тест по теме Электрический ток
Тест по теме Электрический ток Газовые законы
Газовые законы Технология и организация судоремонта
Технология и организация судоремонта Магнитная индукция
Магнитная индукция Газовые законы
Газовые законы ВКР: Организация работ по эксплуатации электропривода главного движения станка модели 16К20ПФ1
ВКР: Организация работ по эксплуатации электропривода главного движения станка модели 16К20ПФ1 Prezentatsia_po_lektsii_6
Prezentatsia_po_lektsii_6 Выбор подходящего трансмиссионного масла
Выбор подходящего трансмиссионного масла Магнитное_поле_в_вакууме
Магнитное_поле_в_вакууме