Содержание
- 2. Термодинамика – раздел физики в котором изучаются макроскопические системы и происходящие в них процессы с энергетической
- 3. Энергия, теплота, работа Энергия – единая количественная мера различных форм движения материи и соответствующих им взаимодействий.
- 4. Работа - процесс передачи энергии системе при воздействии на неё внешних сил. Работа совершается при изменении
- 5. Теплота - это энергия, передаваемая системе в процессе теплообмена с внешними телами. Теплота, как и работа,
- 6. Первый закон термодинамики Изменение энергии системы происходит при сообщении ей теплоты Q и совершении над системой
- 7. С учётом этого: Q= ∆U + A Теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы
- 8. Другая формулировка 1 начала термодинамики Невозможен вечный двигатель 1-ого рода, то есть двигатель, который совершал бы
- 9. Внутренняя энергия системы В общем случае внутренняя энергия системы U состоит из : а) кинетической энергии
- 10. Внутренняя энергия идеального газа состоит только из кинетической энергии теплового движения молекул. Энергия одной молекулы с
- 11. Работа по изменению объёма газа δA>0 - система совершает работу над внешними телами; δA
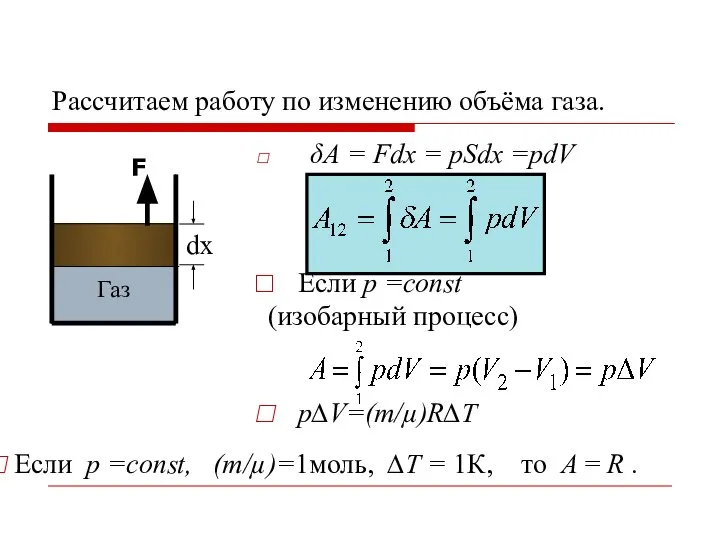
- 12. Рассчитаем работу по изменению объёма газа. δA = Fdх = pSdх =pdV Если р =const (изобарный
- 13. Основы теории теплоёмкости газов 1. Основные понятия Теплоемкость газа [С]=Дж/К Удельная теплоемкость [c0] = Дж/(кг.К) Молярная
- 14. 2. V = const, A=p∆V=0 Qv =cvν∆T , c другой стороны: Qv = ∆U = (i/2)νR∆T
- 15. 3. p = const Qp = cp ν ∆T, c другой стороны: Qp= А + ∆U
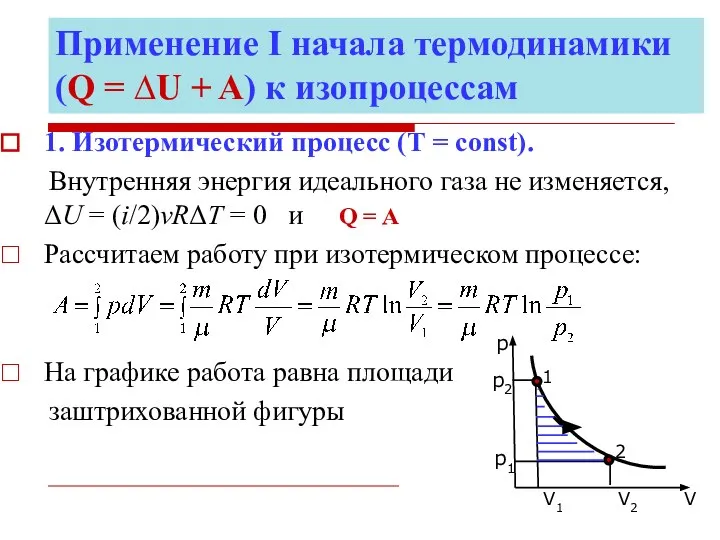
- 16. Применение Ι начала термодинамики (Q = ∆U + A) к изопроцессам 1. Изотермический процесс (Т =
- 17. 2.Изобарический процесс Графически работа определяется площадью заштрихованной фигуры. р=const Q = ∆U + A Q =
- 18. 3. Изохорический процесс V = const A = ∫pdV = 0 Q = ∆U Q =
- 19. 4. Адиабатический процесс Адиабатным (адиабатическим) называется процесс, происходящий в термодинамической системе без теплообмена с окружающими телами.
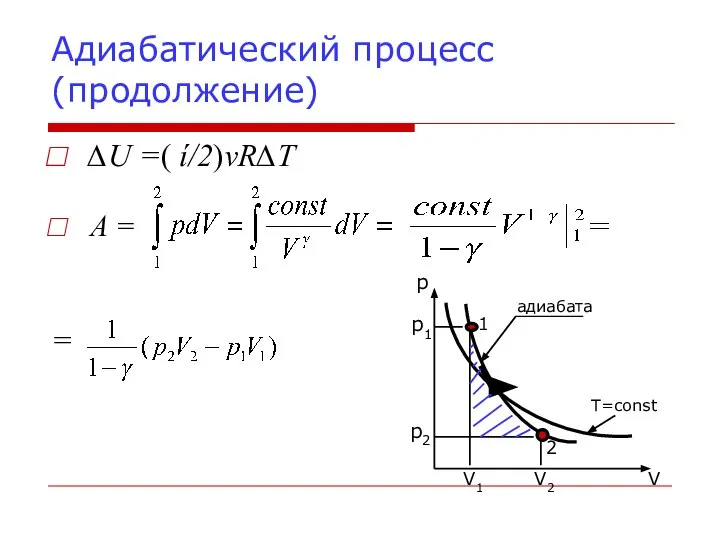
- 20. Адиабатический процесс (продолжение) ∆U =( ί/2)νR∆T = A =
- 21. Обратимые и необратимые процессы Обратимыми называются процессы, которые предполагают возможность возвращения системы в исходное состояние без
- 22. Круговые процессы Если тело из состояния 1 переводится в состояние 2, а затем через другие промежуточные
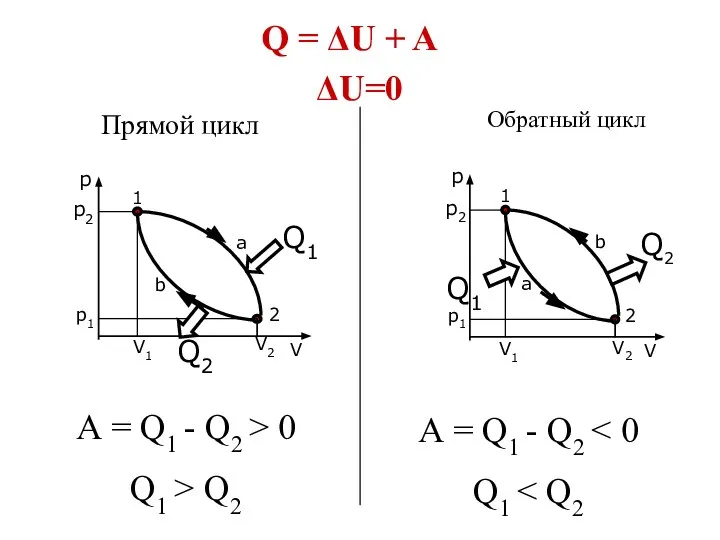
- 23. Обратный цикл Прямой цикл А = Q1 - Q2 > 0 Q1 > Q2 А =
- 24. К.п.д. тепловой машины К.п.д. тепловой машины (η) - это отношение совершаемой за цикл работы А к
- 25. Второе начало термодинамики Клаузиус: не возможен процесс, единственным результатом которого был бы переход теплоты от холодного
- 26. Второе начало термодинамики (продолжение) Невозможен вечный двигатель второго рода (перпетуум мобиле второго рода ), т.е. двигатель,
- 27. Цикл Карно Сади Карно установил, что наибольший к.п.д. имеет процесс, состоящий из двух изотерм и двух
- 28. Цикл Карно (продолжение) К.п.д. цикла Карно
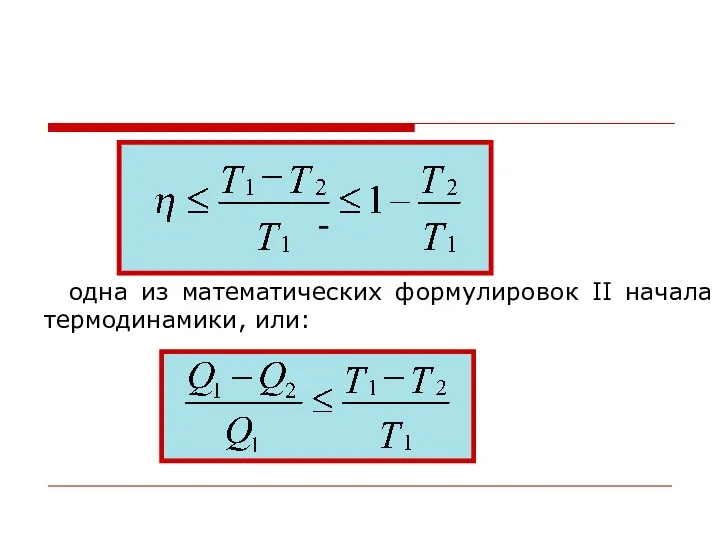
- 29. - одна из математических формулировок II начала термодинамики, или:
- 30. Приведенное количество теплоты Отношение количества теплоты Q, полученной или отданной системой (телом) при изотермическом процессе к
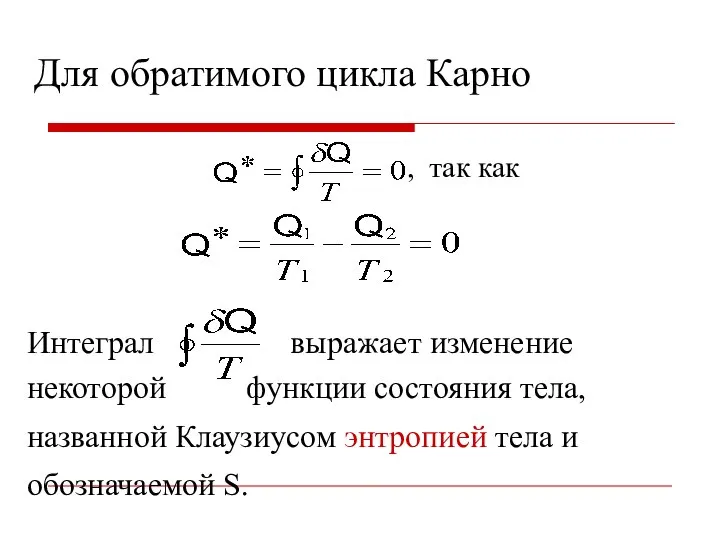
- 31. Интеграл выражает изменение некоторой функции состояния тела, названной Клаузиусом энтропией тела и обозначаемой S. , так
- 32. Энтропия – функция состояния системы Энтропия изолированной системы при любых происходящих в ней процессах не может
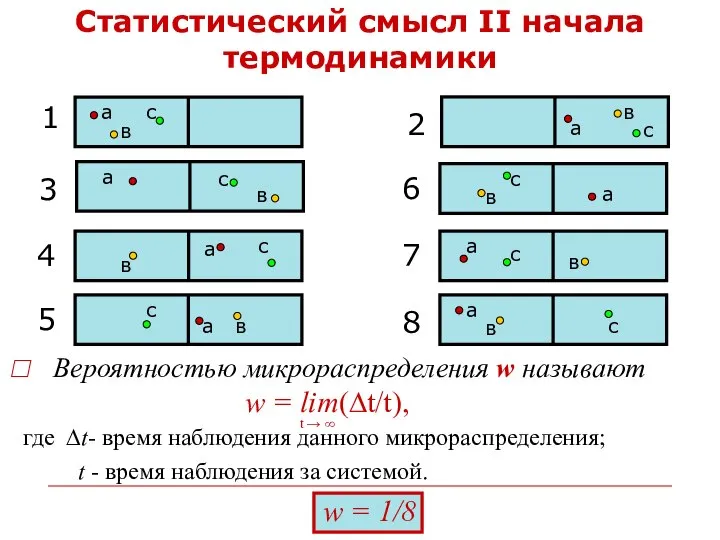
- 33. Статистический смысл II начала термодинамики Вероятностью микрораспределения w называют
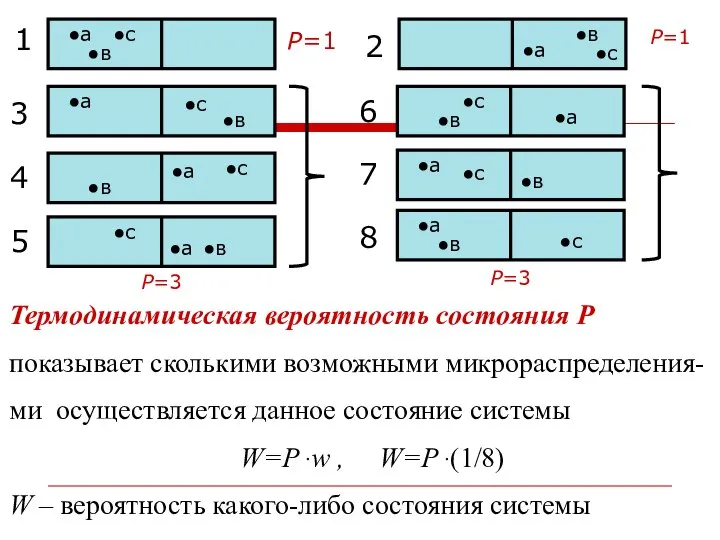
- 34. Р=3 Р=3 Р=1 Р=1 Термодинамическая вероятность состояния Р показывает сколькими возможными микрораспределения- ми осуществляется данное состояние
- 35. Больцман постулировал, что между энтропией и термодинамической вероятностью существует связь: S = k lnР где k
- 36. Статистический смысл второго начала термодинамики Закон возрастания энтропии выражает постоянную тенденцию системы к переходу в более
- 38. Скачать презентацию










![Основы теории теплоёмкости газов 1. Основные понятия Теплоемкость газа [С]=Дж/К Удельная теплоемкость](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/988712/slide-12.jpg)
















 Құрамында талшықтары көп полимерлі композитті наноматериалдар
Құрамында талшықтары көп полимерлі композитті наноматериалдар Давление газа
Давление газа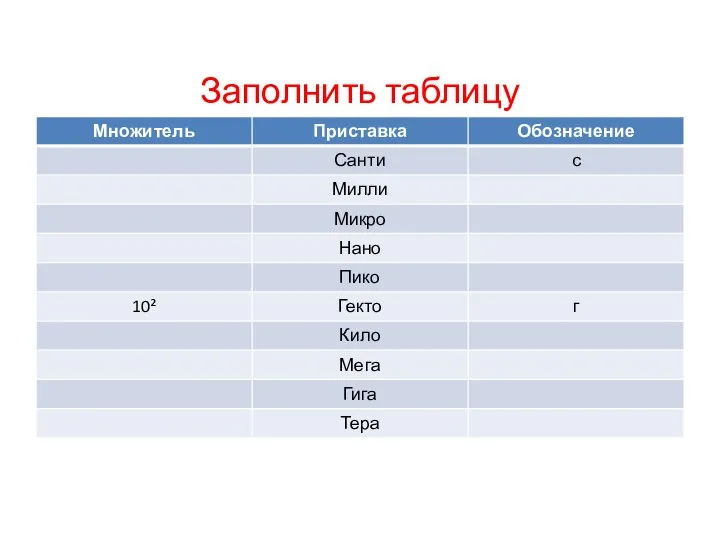 Технические измерения
Технические измерения Физические величины и их измерение. Задания
Физические величины и их измерение. Задания Композиты и нанокомпозиты
Композиты и нанокомпозиты Способы соединения частей: шестеренки
Способы соединения частей: шестеренки Точность и погрешность измерений
Точность и погрешность измерений Аберрации. Сферическая аберрация
Аберрации. Сферическая аберрация Архитектурно-строительная акустика
Архитектурно-строительная акустика Приемы резания и зачистки тонколистового металла и проволоки
Приемы резания и зачистки тонколистового металла и проволоки Движение по окружности. Физика
Движение по окружности. Физика Фізичні основи функціонування систем радіолокації та радіонавігації
Фізичні основи функціонування систем радіолокації та радіонавігації Техническая механика
Техническая механика Скорость тела
Скорость тела Идеальный газ. Абсолютная температура. Макро и микропараметры
Идеальный газ. Абсолютная температура. Макро и микропараметры Исследование агрегатов и систем автомобилей
Исследование агрегатов и систем автомобилей Электромагнетизм
Электромагнетизм Електромагнітні явища
Електромагнітні явища pril1_2 (1)
pril1_2 (1)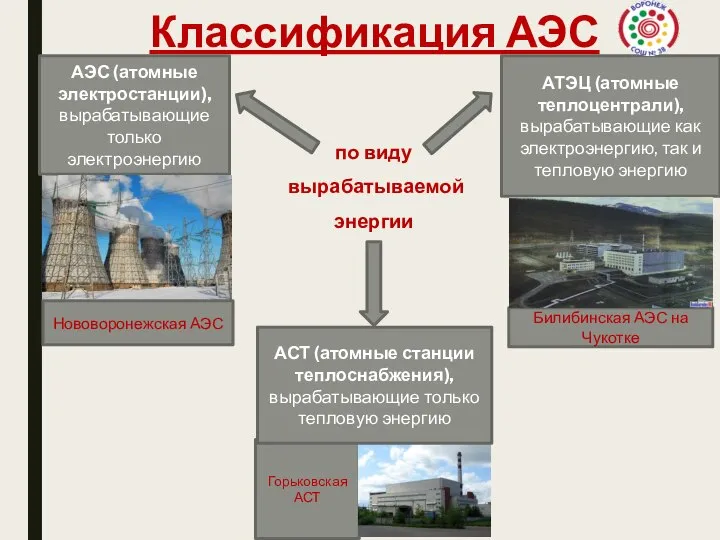 Классификация АЭС
Классификация АЭС Давление
Давление Вимірювальні прилади
Вимірювальні прилади Физические принципы подъема затонувших судов
Физические принципы подъема затонувших судов Возникновение и разнообразие звуков
Возникновение и разнообразие звуков Проектная работа по физике на тему Преобразование электрической энергии в механическую. Сила Ампера
Проектная работа по физике на тему Преобразование электрической энергии в механическую. Сила Ампера Большой адронный коллайдер - путь к апокалипсису или прогрессу?
Большой адронный коллайдер - путь к апокалипсису или прогрессу? 908906
908906 Магнитное поле
Магнитное поле