Электричество и магнетизм. Магнитные свойства вещества

Лекция №13. Магнитные свойства вещества.
13.1. Магнитные моменты электронов и атомов.
13.2. Атом в магнитном поле.
13.3. Магнитное поле в веществе.
13.4. Диамагнетики и парамагнетики в магнитном поле.
13.5. Ферромагнетики.

13.1. Магнитные моменты электронов и атомов
Различные среды при рассмотрении их магнитных свойств называют магнетики.
Все вещества в той или иной мере взаимодействуют с магнитным полем. У некоторых материалов магнитные свойства сохраняются и в отсутствие внешнего магнитного поля.
Намагничивание материалов происходит за счет токов, циркулирующих внутри атомов – вращения электронов и движения их в атоме. «амперовские токи».

В отсутствие внешнего магнитного поля магнитные моменты атомов вещества ориентированы обычно беспорядочно, так что создаваемые ими магнитные поля компенсируют друг друга.

При наложении внешнего магнитного поля атомы стремятся сориентироваться своими магнитными моментами
по направлению внешнего магнитного поля, и тогда компенсация магнитных моментов нарушается, тело приобретает магнитные свойства – намагничивается.

Все тела при внесении их во внешнее магнитное поле намагничиваются в той или иной степени, т.е. создают собственное магнитное поле, которое накладывается на внешнее магнитное поле.
Магнитные свойства вещества определяются магнитными свойствами электронов и атомов.

Магнетики состоят из атомов, которые в свою очередь состоят из положительных ядер и, условно говоря, вращающихся вокруг них электронов.

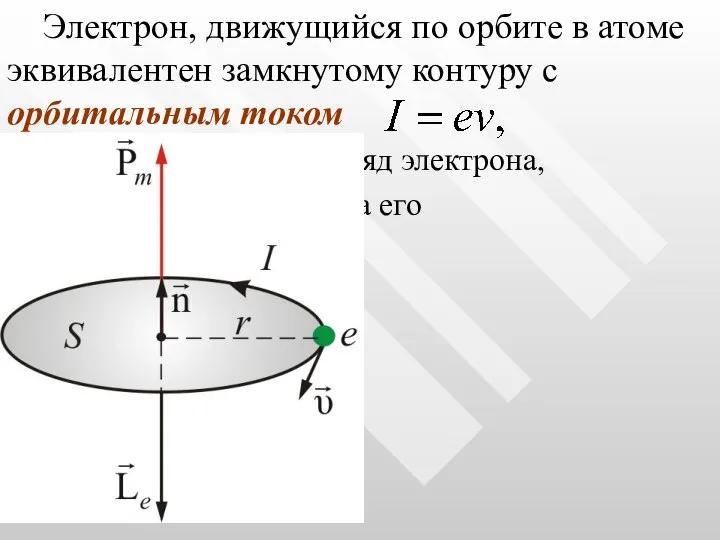
Электрон, движущийся по орбите в атоме эквивалентен замкнутому контуру с орбитальным током где е – заряд электрона,
ν – частота его вращения по орбите.

Орбитальному току соответствует орбитальный магнитный момент электрона
где S – площадь орбиты,
– единичный вектор нормали к S,
– скорость электрона.
Электрон, движущийся по орбите имеет орбитальный момент импульса Lе , который имеет противоположное направление по отношению к Pm и связан с ним соотношением:

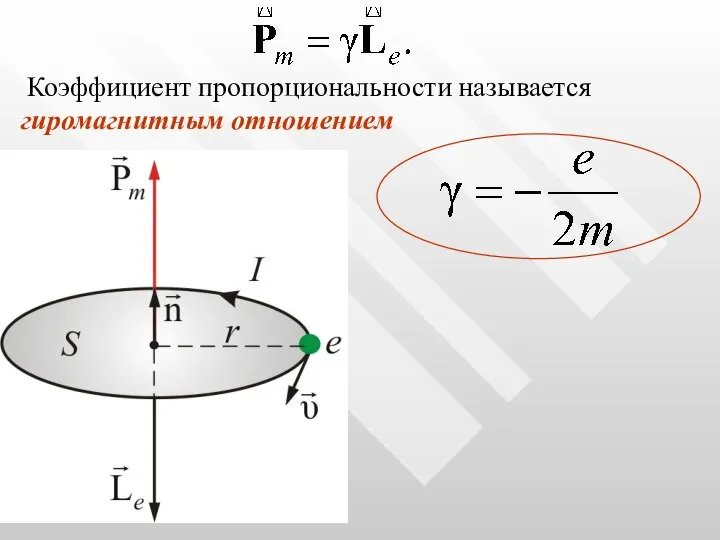
Коэффициент пропорциональности называется гиромагнитным отношением

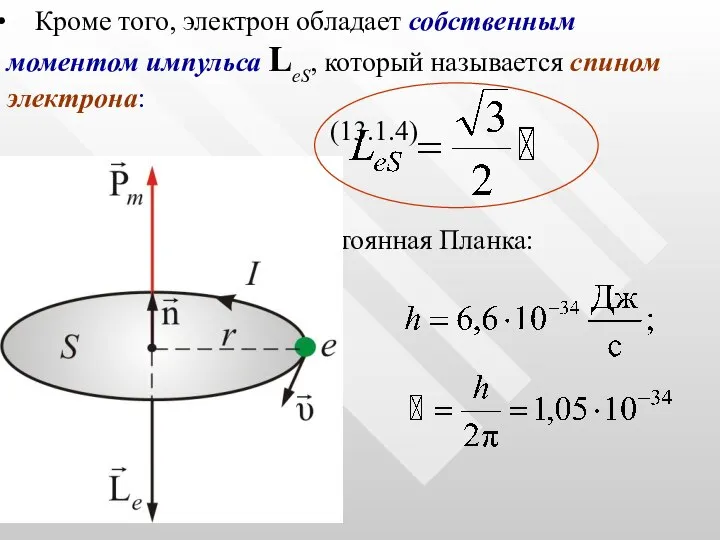
Кроме того, электрон обладает собственным моментом импульса LеS, который называется спином электрона:
(13.1.4)
где h постоянная Планка:

Спину электрона LeS соответствует спиновый магнитный момент электрона PmS, направленный в противоположную сторону:
(13.1.5)
Величину γS называют гиромагнитным отношением спиновых моментов
(13.1.6)

Проекция спинового магнитного момента электрона на направление вектора индукции магнитного поля может принимать только одно из следующих двух значений
(13.1.7)
где μБ – квантовый магнитный момент электрона – магнетон Бора.

Орбитальным магнитным моментом Рm атома называется геометрическая сумма орбитальных магнитных моментов всех электронов атома
(13.1.8)
где Z – число всех электронов в атоме – порядковый номер элемента в периодической системе Менделеева.
Орбитальным моментом импульса L атома называется геометрическая сумма моментов импульса всех электронов атома:
(13.1.9)
Более подробно вышеназванные характеристики мы обсудим в разделе «Атомная и ядерная физика».

Общий орбитальный момент атома равен векторной сумме магнитных моментов (орбитальных и спиновых) всех электронов:

13.2. Атом в магнитном поле.
В магнитное поле с индукцией на электрон, движущийся по орбите эквивалентной замкнутому контуру с током, действует момент сил :
(13.2.1)
При этом изменяется орбитальный момент импульса электрона:
(13.2.2)
Аналогично изменяется вектор орбитального магнитного момента электрона
(13.2.3)

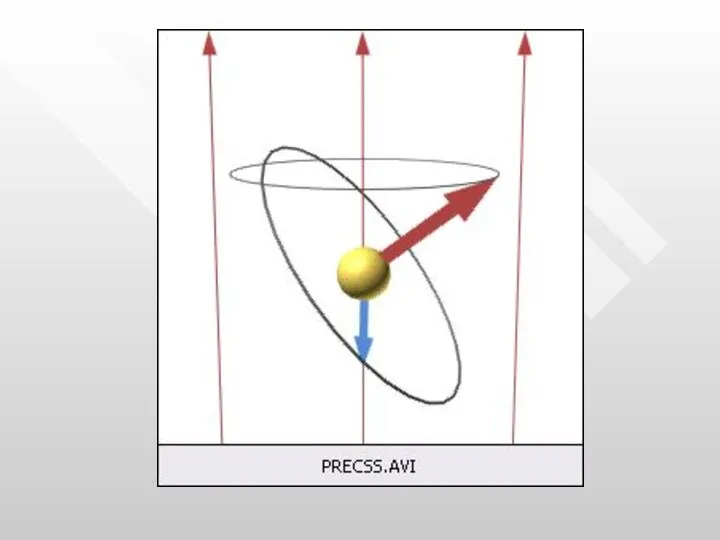
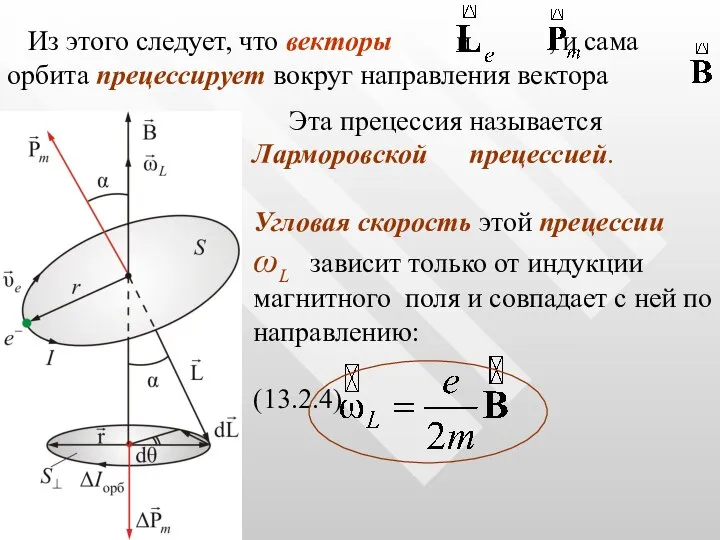
Из этого следует, что векторы и , и сама орбита прецессирует вокруг направления вектора
Эта прецессия называется Ларморовской прецессией.
Угловая скорость этой прецессии ωL зависит только от индукции магнитного поля и совпадает с ней по направлению:
(13.2.4)

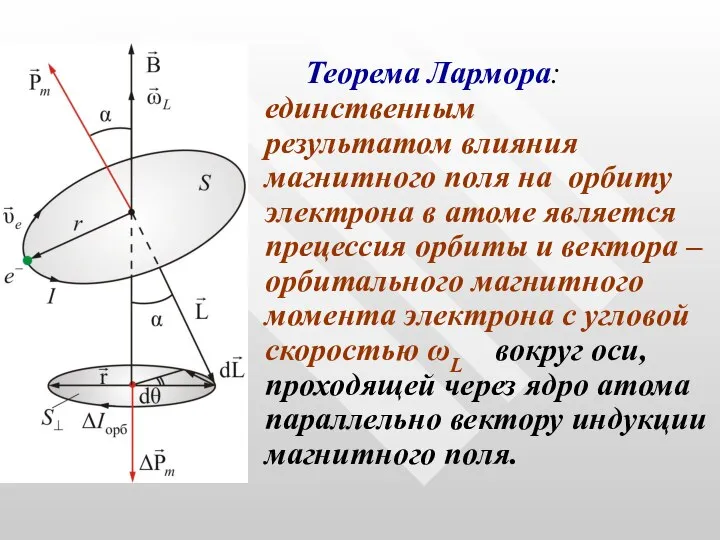
Теорема Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора – орбитального магнитного момента электрона с угловой скоростью ωL вокруг оси, проходящей через ядро атома параллельно вектору индукции магнитного поля.

Прецессия орбиты электрона в атоме приводит к появлению дополнительного орбитального тока, направленного противоположно току I
и соответствующего ему наведенного орбитального магнитного момента ΔPm
где – площадь проекции орбиты электрона на плоскость, перпендикулярную вектору .
Знак минус говорит, что Δ противоположен вектору .

Общий орбитальный момент атома в магнитном поле равен векторной сумме:
Первое слагаемое – полный магнитный момент равен нулю.
Тогда орбитальный момент атома
Z – число электронов в атоме

13.3. Магнитное поле в веществе.
При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки.
Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел.
Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах.

Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего
или собственного, магнитного поля, создаваемого микротоками.
Характеризует магнитное поле в веществе вектор , равный геометрической сумме
создаваемого макротоками и
создаваемого микротоками:

Количественной характеристикой намагниченного состояния вещества служит – намагниченность , равная отношению магнитного момента малого объема вещества к величине этого объема:
Где – магнитный момент i-го атома из числа n атомов, содержащихся в объеме ΔV.

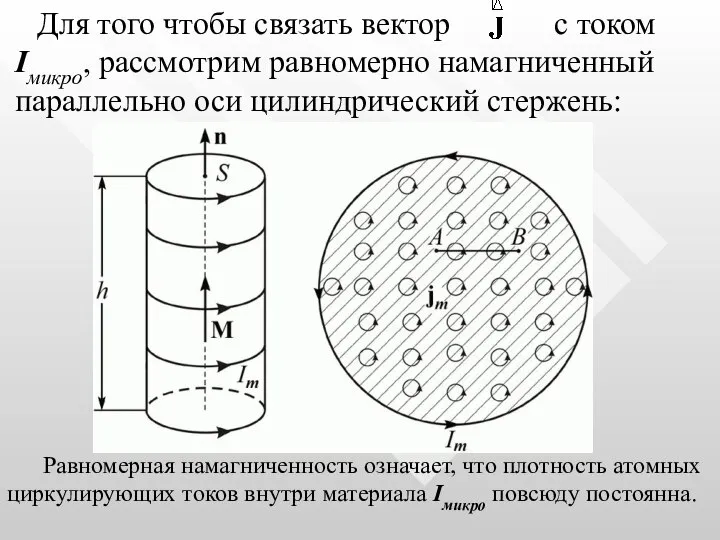
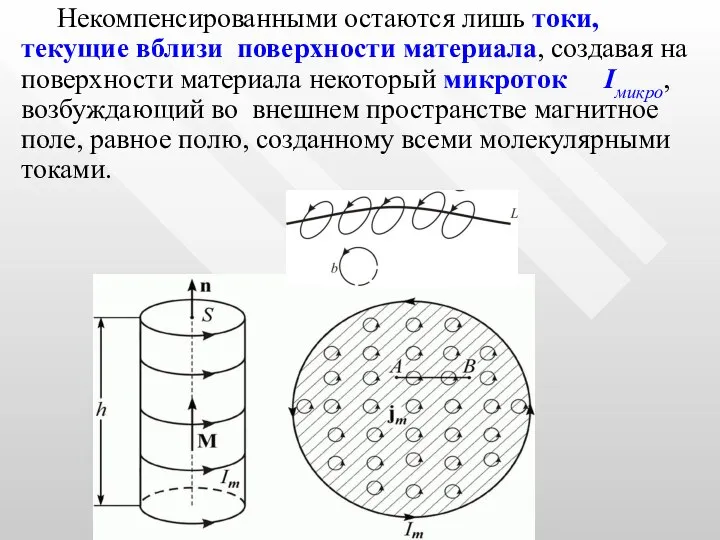
Для того чтобы связать вектор с током Iмикро, рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень:
Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала Iмикро повсюду постоянна.

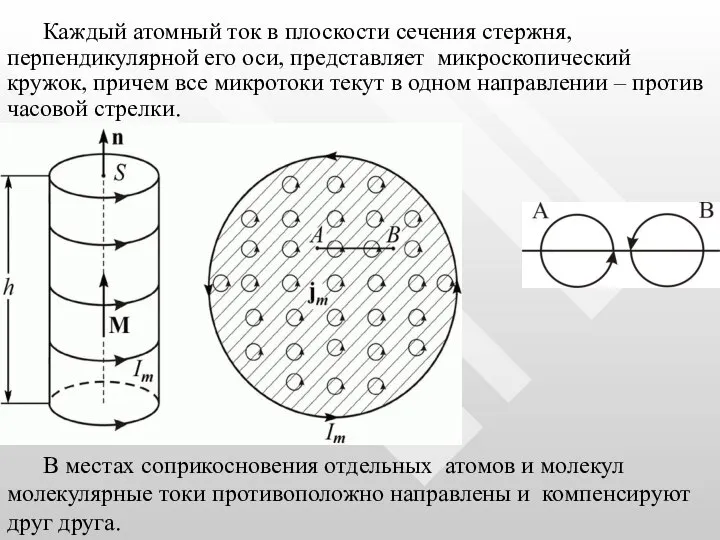
Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки.
В местах соприкосновения отдельных атомов и молекул молекулярные токи противоположно направлены и компенсируют друг друга.

Некомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый микроток Iмикро, возбуждающий во внешнем пространстве магнитное поле, равное полю, созданному всеми молекулярными токами.

Закон полного тока для магнитного поля в веществе:
где Iмикро и Iмакро – алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L.
Как видно из рис. вклад в Iмикро дают только те молекулярные токи, которые нанизаны на замкнутый контур L.

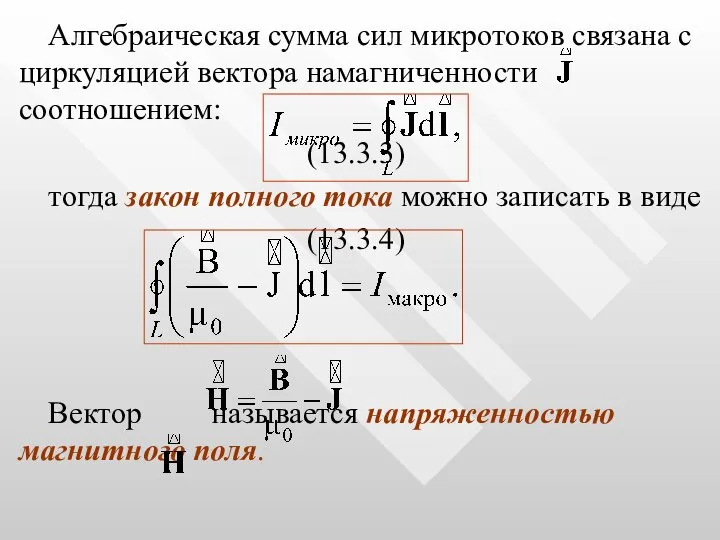
Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением:
(13.3.3)
тогда закон полного тока можно записать в виде
(13.3.4)
Вектор называется напряженностью магнитного поля.

Таким образом, закон полного тока для магнитного поля в веществе утверждает, что циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность натянутую на этот контур:
(13.3.5)
Этот закон полного тока в интегральной форме.
В дифференциальной форме его можно записать:
(13.3.6)

Намагниченность изотропной среды с напряженностью связаны соотношением
(13.3.7)
где – магнитная восприимчивость среды.
коэффициент пропорциональности, характеризующий магнитные свойства вещества.

13.4.Диамагнетики и парамагнетики в магнитном поле.
Микроскопические плотности токов в намагниченном веществе чрезвычайно сложны и сильно изменяются даже в пределах одного атома. Но нас интересуют средние магнитные поля, созданные большим числом атомов.
Как было сказано характеристикой намагниченного состояния вещества служит векторная величина – намагниченность , равная отношению магнитного момента малого объема вещества к величине этого объема:
(13.4.1)
Где – магнитный момент i-го атома из числа n атомов, содержащихся в объеме ΔV.

Магнетики можно разделить на три основные группы: диамагнетики, парамагнетики и ферромагнетики.
Если магнитное поле слабо усиливается в веществе, то такое вещество называется парамагнетиком
(Се3+, Рr3+, Ti3+, V3+, Fe2+, Mg2+, Li, Na)
если ослабевает, то это диамагнетик
(Bi, Cu, Ag, Au и др.).
Вещества, обладающие сильными магнитными свойствами называются ферромагнетиками
(Fe, Co, Ni и пр.).
постоянные магниты.

Диамагнетизм (от греч. dia – расхождение) − свойство веществ намагничиваться навстречу приложенному магнитному полю.
Диамагнетиками называются вещества, магнитные моменты атомов которых в отсутствии внешнего поля равны нулю, т.к. магнитные моменты всех электронов атома взаимно скомпенсированы (например инертные газы, водород, азот, NaCl, Bi, Cu, Ag, Au и др.).
При внесении диамагнитного вещества в магнитное поле его атомы приобретают наведенные магнитные моменты ΔPm направленные противоположно вектору .

Вектор намагниченности диамагнетика равен
(13.4.2)
Для всех диамагнетиков
Вектор магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле направлен в сторону, противоположную (В отличии от диэлектрика в электрическом поле).
У диамагнетиков
–магнитная восприимчивость среды.

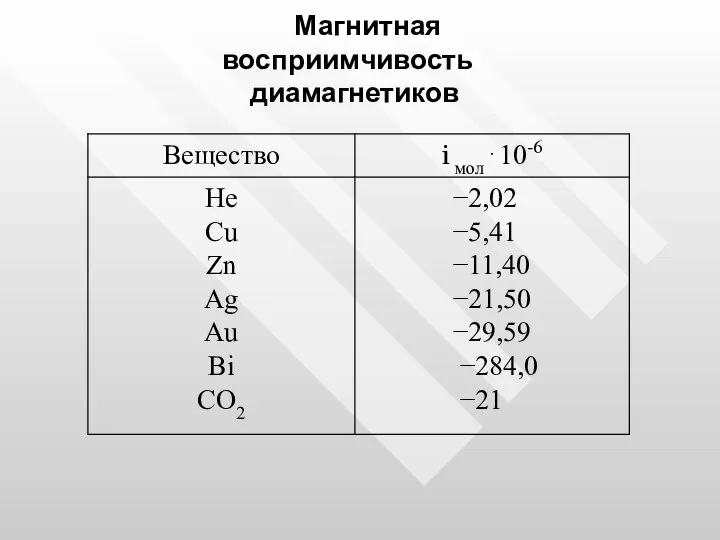
Магнитная восприимчивость
диамагнетиков

Парамагнетизм (от греч. para – возле) − свойство веществ во внешнем магнитном поле намагничиваться в направлении этого поля поэтому внутри парамагнетика к действию внешнего поля прибавляется действие наведенного внутреннего поля.
Парамагнетиками называются вещества, атомы которых имеют в отсутствии внешнего магнитного поля, отличный от нуля магнитный момент .
Эти вещества намагничиваются в направлении вектора .

К парамагнетикам относятся многие щелочные металлы, кислород О2, оксид азота NO, хлорное железо FeCI2 Се3+, Рr3+, Ti3+, V3+, Fe2+, Mg2+, Li, Na и др.
В отсутствии внешнего магнитного поля намагниченность парамагнетика J = 0, так как векторы разных атомов ориентированы беспорядочно.
При внесении парамагнетика во внешнее магнитное поле, происходит преимущественная ориентация собственных магнитных моментов атомов по направлению поля, так что парамагнетик намагничивается.
Значения для парамагнетиков положительны ( ) и находятся в пределах ~ 10–5 ÷ 10–3, то есть, как и у диамагнетиков.

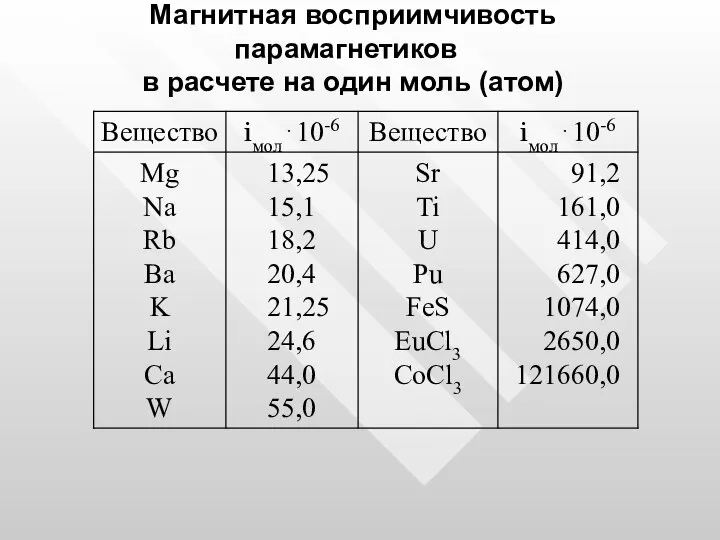
Магнитная восприимчивость парамагнетиков
в расчете на один моль (атом)

13.5. Ферромагнетики.
К ферромагнетикам (ferrum – железо) относятся вещества, магнитная восприимчивость которых положительна и очень велика.
Намагниченность и магнитная индукция ферромагнетиков растут с увеличением напряженности магнитного поля нелинейно, и в полях ~ 8⋅103 А/м намагниченность ферромагнетиков достигает предельного значения , а вектор магнитной индукции растет линейно с :
Наличие у ферромагнетиков самопроизвольного магнитного момента в отсутствие внешнего магнитного поля означает, что электронные спины и магнитные моменты атомных носителей магнетизма ориентированы в веществе упорядоченным образом.

Ферромагнетики это вещества, обладающие самопроизвольной намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, температуры.
У ферромагнетиков магнитная восприимчивость положительна и очень велика = 104 ÷ 105.
В ферромагнетиках происходит резкое усиление внешних магнитных полей.
Для ферромагнетиков сложным образом зависит от величины магнитного поля.
Типичными ферромагнетиками являются Fe, Co, Ni, Gd,, Dy, Ho, Er, Tm, а также соединения ферромагнитных материалов с неферромагнитными: Fe3Al, Ni3Mn, ZnCMn3
Ферромагнетики, в отличие от слабо магнитных диа- и парамагнетиков, являются сильно магнитными веществами: внутреннее магнитное поле в них может в сотни раз превосходить внешнее поле.

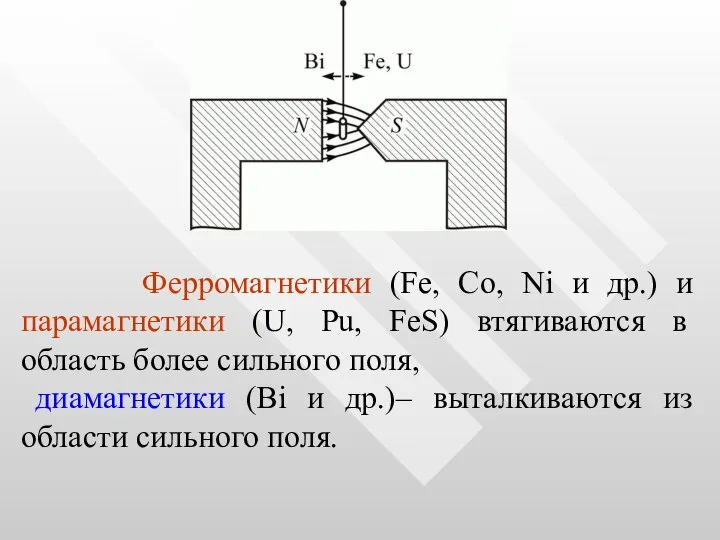
Ферромагнетики (Fe, Co, Ni и др.) и парамагнетики (U, Pu, FeS) втягиваются в область более сильного поля,
диамагнетики (Bi и др.)– выталкиваются из области сильного поля.

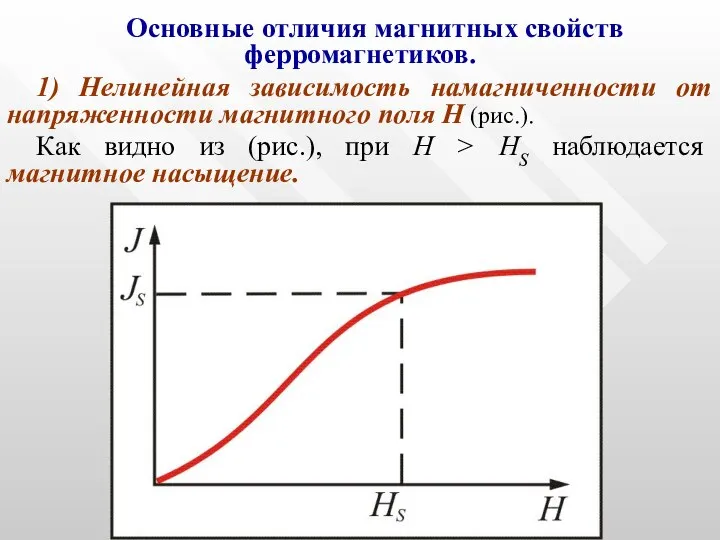
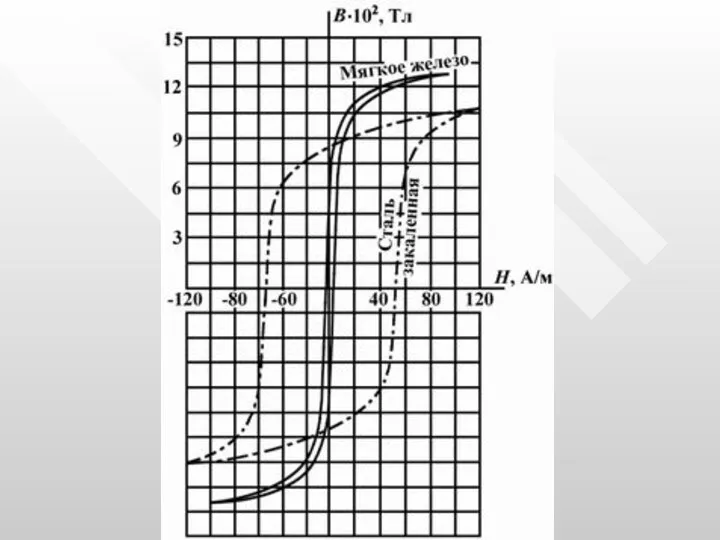
Основные отличия магнитных свойств ферромагнетиков.
1) Нелинейная зависимость намагниченности от напряженности магнитного поля Н (рис.).
Как видно из (рис.), при Н > HS наблюдается магнитное насыщение.
Рис. 13.5

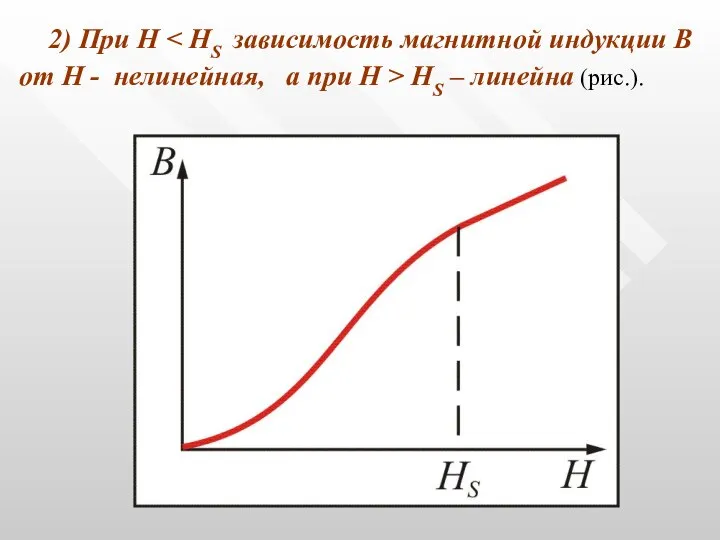
2) При Н < HS зависимость магнитной индукции В от Н - нелинейная, а при Н > HS – линейна (рис.).
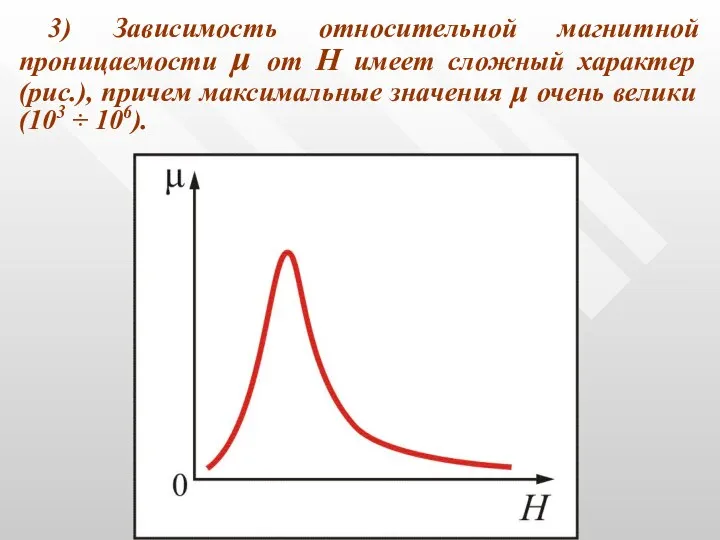
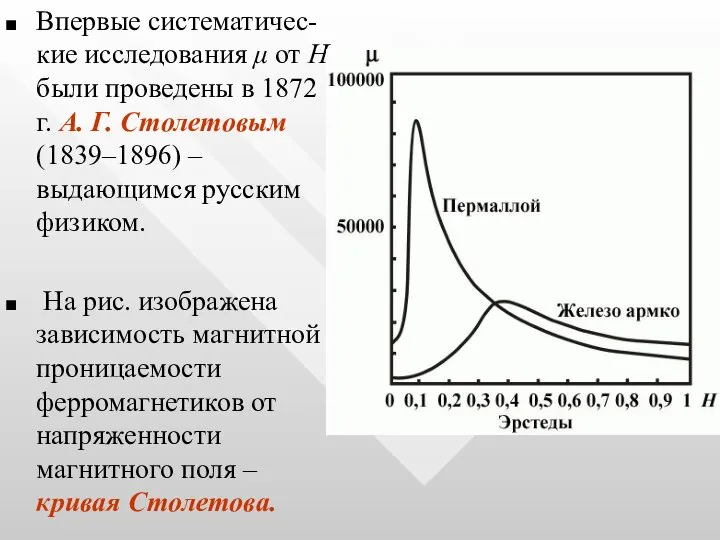
Рис. 13.6

3) Зависимость относительной магнитной проницаемости μ от Н имеет сложный характер (рис.), причем максимальные значения μ очень велики (103 ÷ 106).
Рис. 13.7

Впервые систематичес-кие исследования μ от Н были проведены в 1872 г. А. Г. Столетовым (1839–1896) – выдающимся русским физиком.
На рис. изображена зависимость магнитной проницаемости ферромагнетиков от напряженности магнитного поля – кривая Столетова.

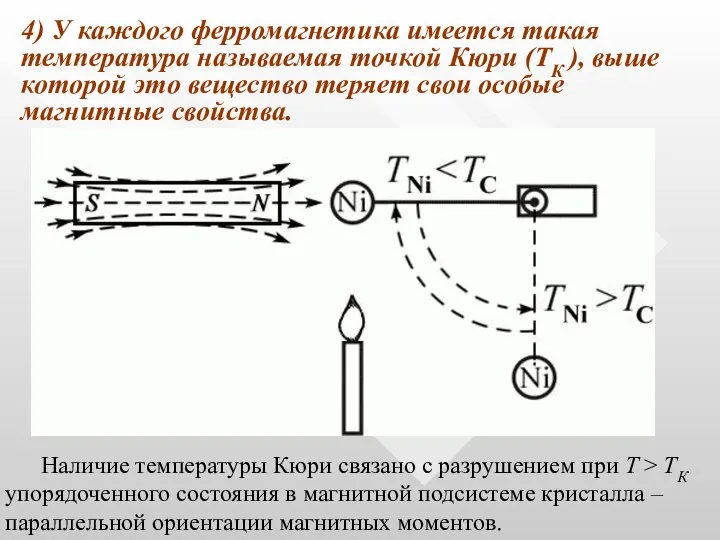
4) У каждого ферромагнетика имеется такая температура называемая точкой Кюри (ТК ), выше которой это вещество теряет свои особые магнитные свойства.
Наличие температуры Кюри связано с разрушением при T > TК упорядоченного состояния в магнитной подсистеме кристалла – параллельной ориентации магнитных моментов.

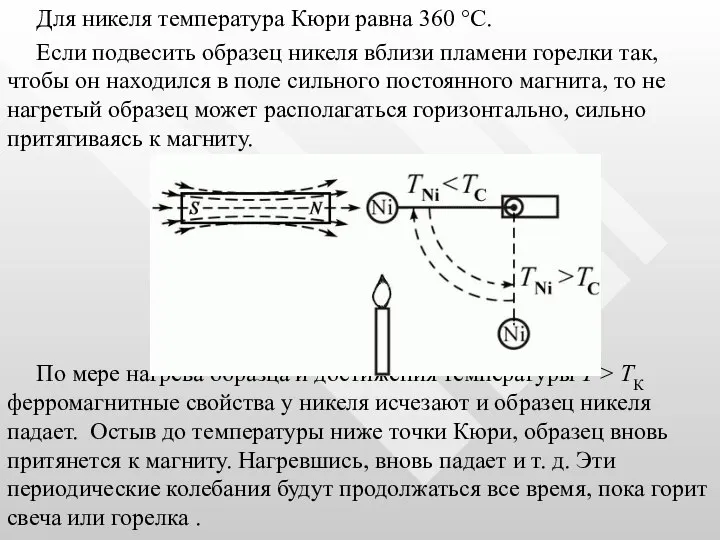
Для никеля температура Кюри равна 360 °С.
Если подвесить образец никеля вблизи пламени горелки так, чтобы он находился в поле сильного постоянного магнита, то не нагретый образец может располагаться горизонтально, сильно притягиваясь к магниту.
По мере нагрева образца и достижения температуры T > TК ферромагнитные свойства у никеля исчезают и образец никеля падает. Остыв до температуры ниже точки Кюри, образец вновь притянется к магниту. Нагревшись, вновь падает и т. д. Эти периодические колебания будут продолжаться все время, пока горит свеча или горелка .

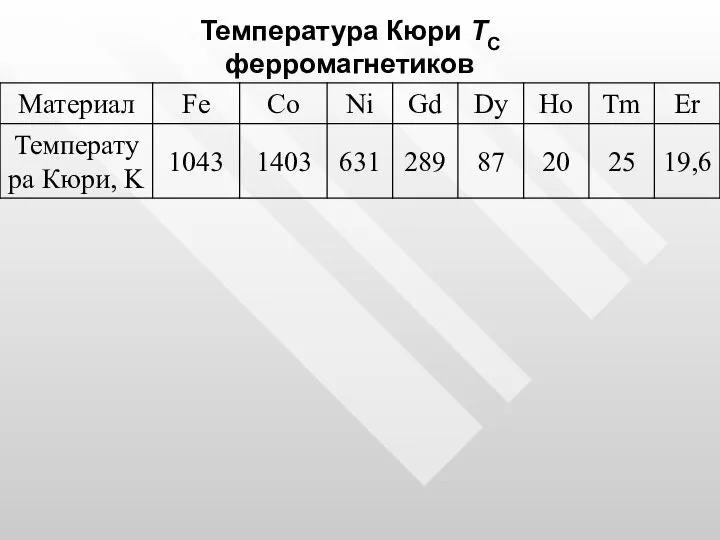
Температура Кюри TС ферромагнетиков

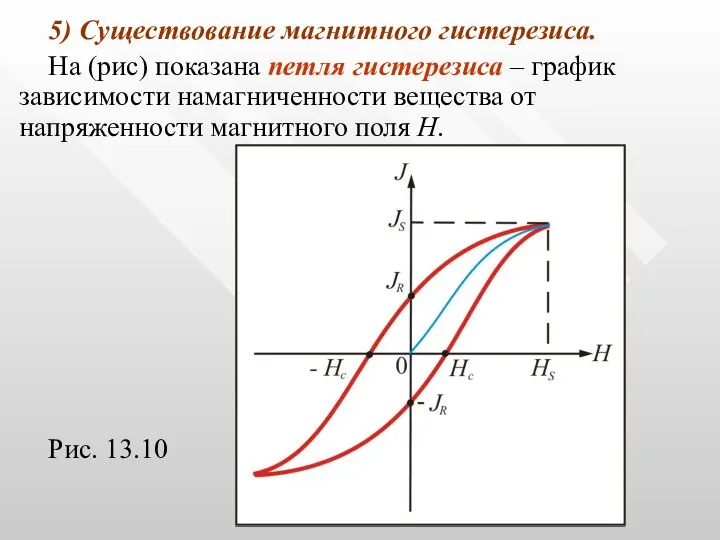
5) Существование магнитного гистерезиса.
На (рис) показана петля гистерезиса – график зависимости намагниченности вещества от напряженности магнитного поля Н.
Рис. 13.10

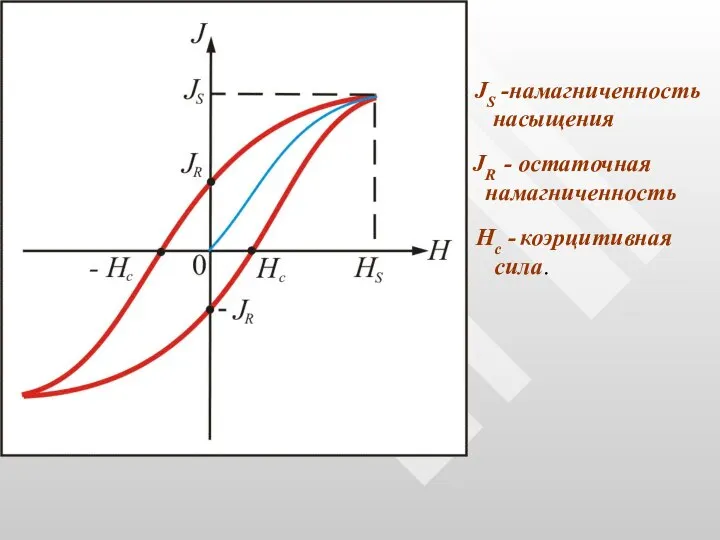
JR - остаточная
намагниченность
JS -намагниченность
насыщения
Нс - коэрцитивная
сила.

Намагниченность JS при Н = НS называется намагниченность насыщения.
Намагниченность JR при Н = 0 называется остаточной намагниченностью (что служит для создания постоянных магнитов)
Напряженность Нс магнитного поля, полностью размагниченного ферромагнетика, называется коэрцитивной силой. Она характеризует способность ферромагнетика сохранять намагниченное состояние.
Большой коэрцитивной силой (широкой петлей гистерезиса) обладают магнитотвердые материалы, используемые для изготовления постоянных магнитов
Малую коэрцитивную силу имеют магнитомягкие материалы (используются для изготовления трансформаторов).

Измерение гиромагнитного отношения для ферромагнетиков показали, что
элементарными носителями магнетизма в ферромагнетиках являются спиновые магнитные моменты электронов.

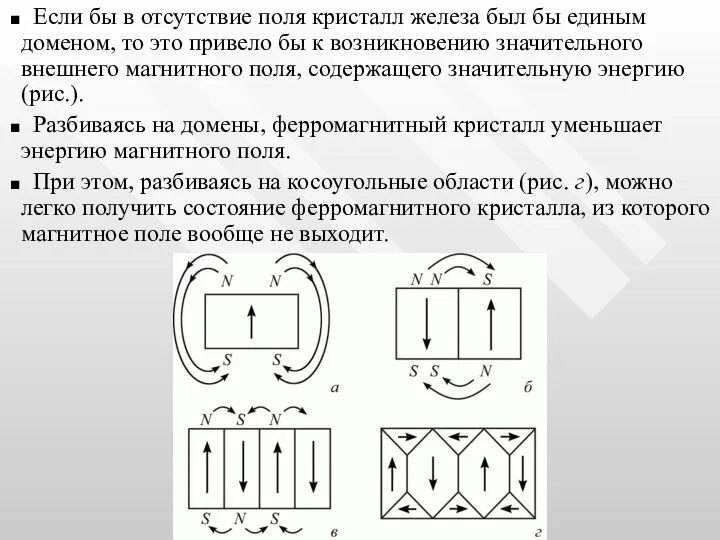
Самопроизвольно намагничиваются лишь очень маленькие монокристаллы ферромагнитных материалов, например никеля или железа.
Оказывается, что большой исходный кусок железа разбит на множество очень маленьких (10–2 ÷ 10–3 см), полностью намагниченных областей – доменов.
Векторы намагниченности доменов в отсутствие внешнего магнитного поля ориентированы таким образом, что полный магнитный момент ферромагнитного материала равен нулю.

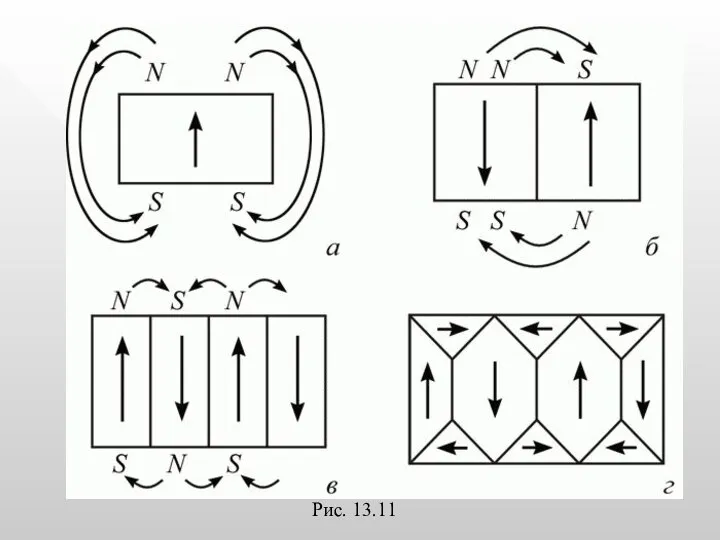
Если бы в отсутствие поля кристалл железа был бы единым доменом, то это привело бы к возникновению значительного внешнего магнитного поля, содержащего значительную энергию (рис.).
Разбиваясь на домены, ферромагнитный кристалл уменьшает энергию магнитного поля.
При этом, разбиваясь на косоугольные области (рис. г), можно легко получить состояние ферромагнитного кристалла, из которого магнитное поле вообще не выходит.

Рис. 13.11

Разбиение всего кристалла на домены уменьшает общую энергию системы пропорционально объему кристалла.
В монокристалле реализуется такое разбиение на доменные структуры, которое соответствует минимуму свободной энергии ферромагнетика.
Если поместить ферромагнетик, разбитый на домены, во внешнее магнитное поле, то в нем начинается движение доменных стенок. Они перемещаются таким образом, чтобы областей с ориентацией вектора намагниченности по полю стало больше, чем областей с противоположной ориентацией.
Такое движение доменных стенок понижает энергию ферромагнетика во внешнем магнитном поле.
По мере нарастания магнитного поля весь кристалл превращается в один большой домен с магнитным моментом, ориентированным по полю (рис.).

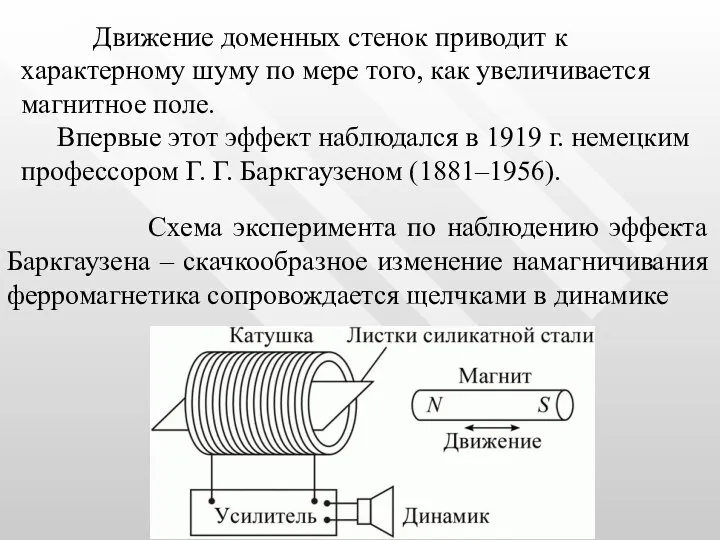
Схема эксперимента по наблюдению эффекта Баркгаузена – скачкообразное изменение намагничивания ферромагнетика сопровождается щелчками в динамике
Движение доменных стенок приводит к характерному шуму по мере того, как увеличивается магнитное поле.
Впервые этот эффект наблюдался в 1919 г. немецким профессором Г. Г. Баркгаузеном (1881–1956).

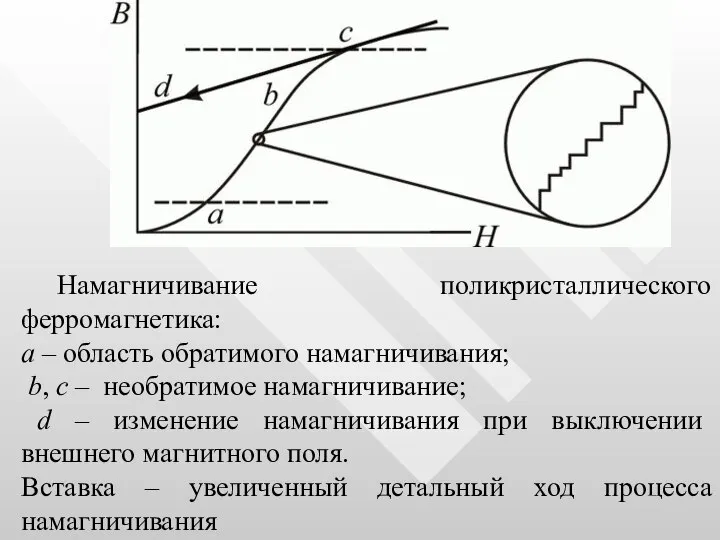
Намагничивание поликристаллического ферромагнетика:
a – область обратимого намагничивания;
b, c – необратимое намагничивание;
d – изменение намагничивания при выключении внешнего магнитного поля.
Вставка – увеличенный детальный ход процесса намагничивания

Ферромагнитные материалы играют огромную роль в самых различных областях современной техники. Магнитомягкие материалы используются в электротехнике при изготовлении трансформаторов, электромоторов, генераторов, в слаботочной технике связи и радиотехнике;
Магнитожесткие материалы применяют при изготовлении постоянных магнитов.
Широкое распространение в радиотехнике, особенно в высокочастотной радиотехнике получили ферриты – ферромагнитные неметаллические материалы – соединения окиси железа (Fe2O3) с окислами других металлов.
Ферриты сочетают ферромагнитные и полупроводниковые свойства, именно с этим связано их применение как магнитных материалов в радиоэлектронике и вычислительной технике.
Ферриты обладают высоким значениями намагниченности и температурами Кюри.

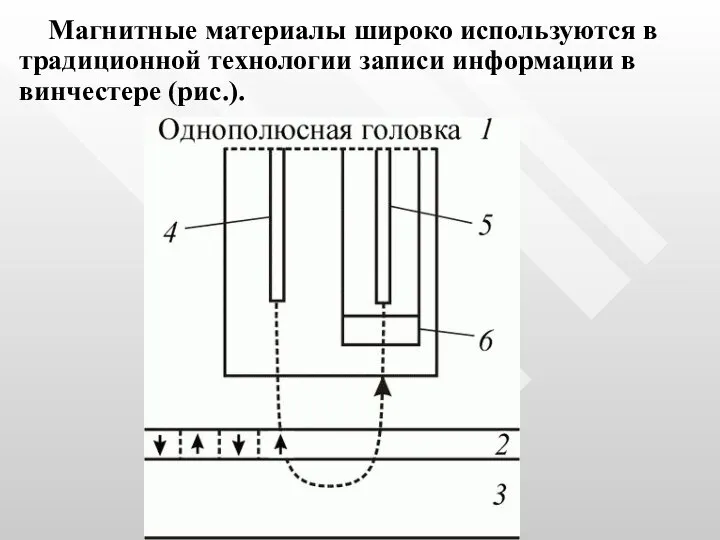
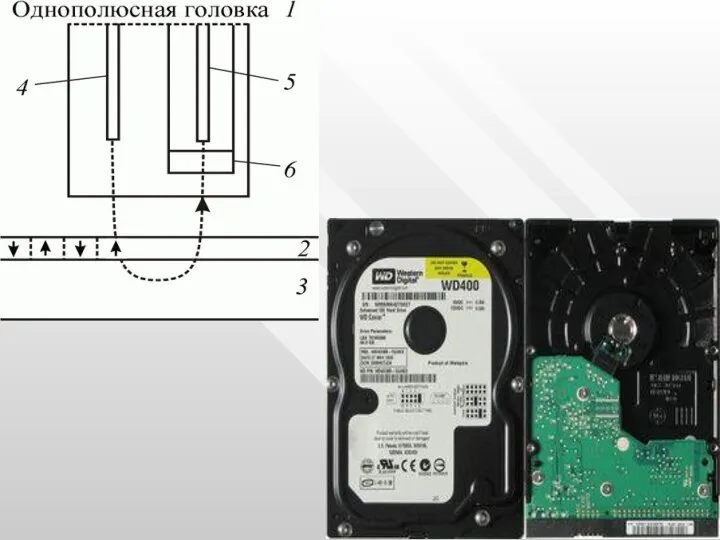
Магнитные материалы широко используются в традиционной технологии записи информации в винчестере (рис.).

Магнитное вещество нанесено тонким слоем на основу твердого диска.
Каждый бит информации представлен группой магнитных доменов (в идеальном случае – одним доменом).
Для перемагничивания домена (изменения направления вектора его намагниченности) используется поле записывающей головки.
Энергия, необходимая для этого, зависит от объема домена и наличия дополнительных стабилизирующих слоев, препятствующих самопроизвольной потере информации.
При этом используется запись на вертикально ориентированные домены и достигается плотность записи до 450 Гб/см2 (в обычных винчестерах в 10 раз меньше).

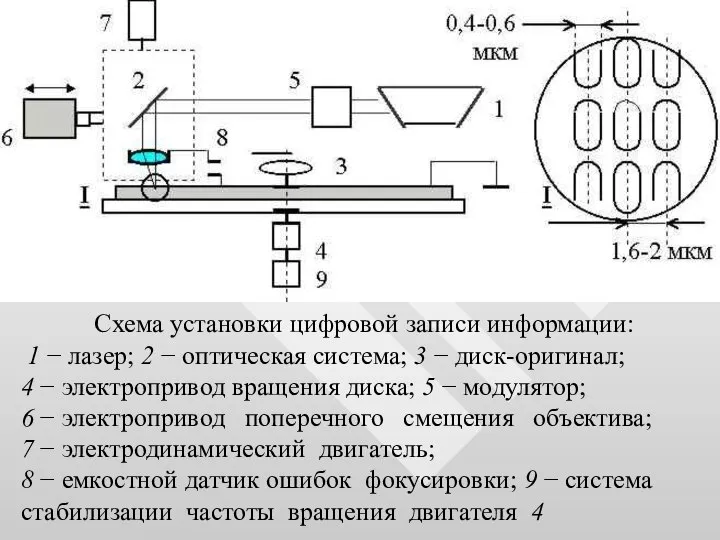
Схема установки цифровой записи информации:
1 − лазер; 2 − оптическая система; 3 − диск-оригинал;
4 − электропривод вращения диска; 5 − модулятор;
6 − электропривод поперечного смещения объектива;
7 − электродинамический двигатель;
8 − емкостной датчик ошибок фокусировки; 9 − система стабилизации частоты вращения двигателя 4

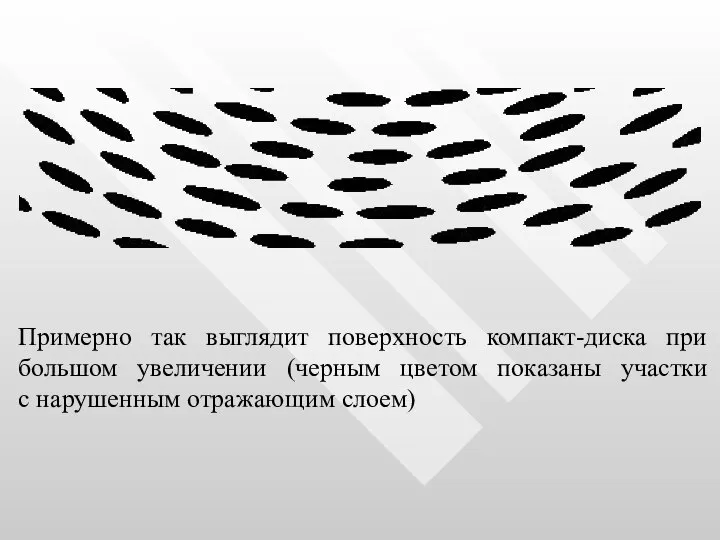
Примерно так выглядит поверхность компакт-диска при большом увеличении (черным цветом показаны участки с нарушенным отражающим слоем)

Структура CD-R диска

В структуре CD-R диска можно выделить пять слоев. Изначально изготавливается пластмассовая основа диска − поликарбонат (Е), которая составляет основную часть CD-R и придает ему необходимую прочность и форму. На готовую пластмассовую форму наносится активный слой (D). Этот слой позволяет осуществлять запись на диск и определяет его надежность и качество считывания информации в дальнейшем. После того, как был нанесен активный слой, диск покрывается специальным слоем светоотражающего материала (C). Завершающим этапом изготовления диска является нанесение защитного слоя (В), на который наносится изображение (А). Основное отличие всех CD-R в слое (D). На сегодняшний день существуют две разновидности красителей для этого слоя, на основе цианина и на основе фталоцианина. Цианиновый краситель обладает сине-зеленым (большинство дисков TDK) или насыщенно синим (Verbatim, серия «Metal Azo») оттенком рабочей поверхности. Фталоцианин, практически бесцветен, с бледным оттенком салатового (диски Rostok Media) или золотистого цвета (печально известные BTC). Сложно сказать, какой из этих двух слоев лучше. Цианиновый краситель более терпим к различным сочетаниям мощности чтения/записи, чем «золотой» фталоцианиновый, но менее устойчив к свету. Фталоцианин − несколько более современная разработка.

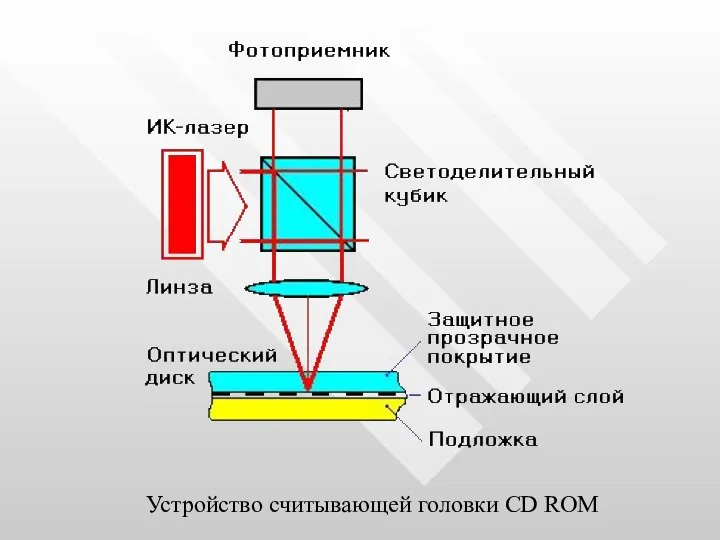
Устройство считывающей головки CD ROM

Схема считывания данных с компакт-диска. Система фокусиpовки включает подвижную линзу (1), приводимую в движение электромагнитной системой Voice Coil, сделанной по аналогии с подвижной системой громкоговорителя. Изменение напряженности магнитного поля, создаваемого катушкой (2), вызывает перемещение подвешенного на упругом держателе (3) магнита (4), к которому крепится линза, и соответственно пеpефокусиpовку лазерного луча. Благодаря малой инерционности такая система эффективно отслеживает вертикальные биения диска даже при значительных скоростях вращения

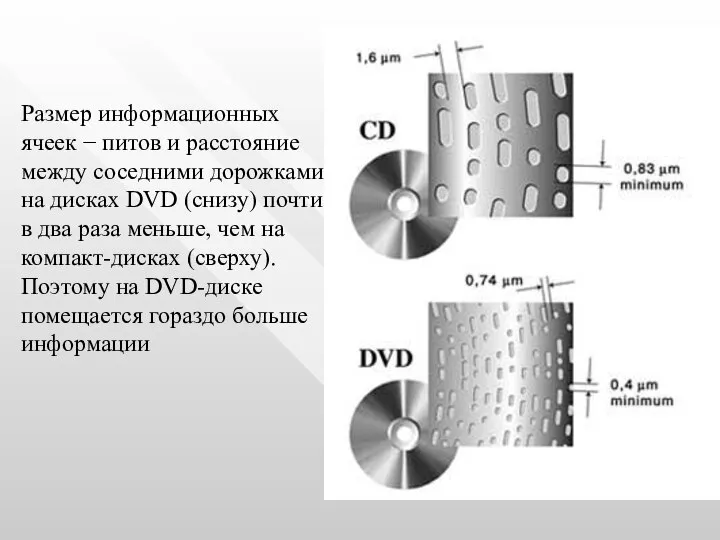
Размер информационных ячеек − питов и расстояние между соседними дорожками на дисках DVD (снизу) почти в два раза меньше, чем на компакт-дисках (сверху). Поэтому на DVD-диске помещается гораздо больше информации

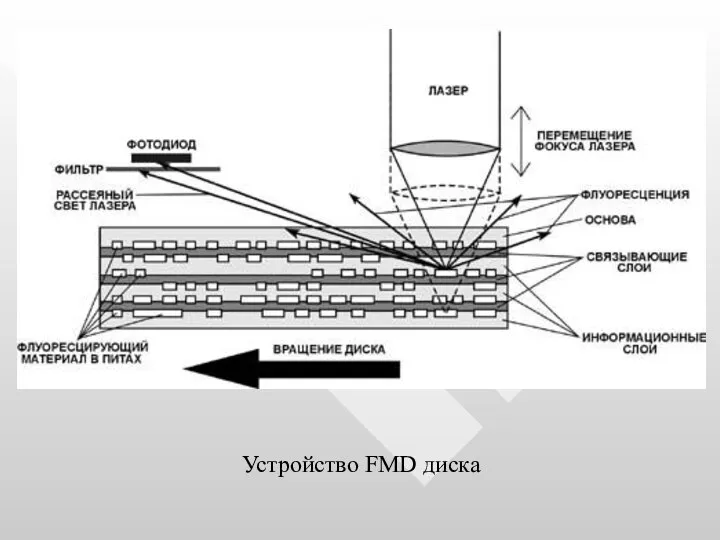
Устройство FMD диска

Сверхпроводники в магнитном поле
Необычными магнитными свойствами обладают сверхпроводники – вещества с бесконечно большой проводимостью или нулевым электрическим сопротивлением.

Куперовские пары электронов в сверхпроводнике образуются и конденсируются в сверхпроводящую жидкость при низких температурах – электронный бозе-конденсат:

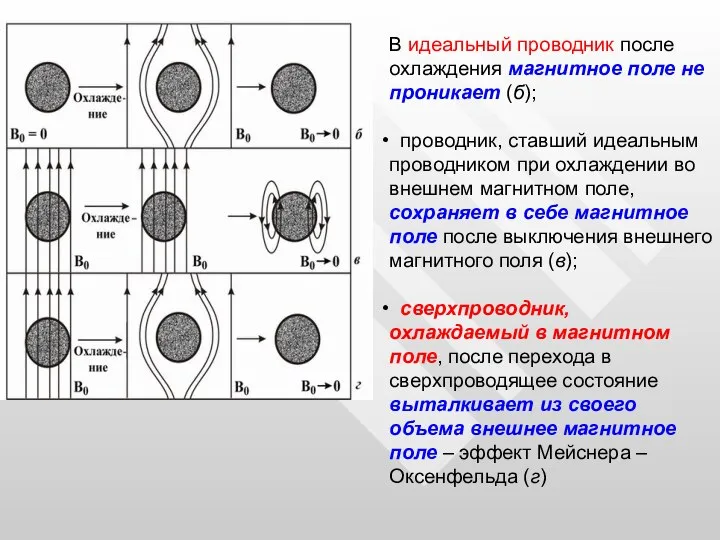
В идеальный проводник после охлаждения магнитное поле не проникает (б);
проводник, ставший идеальным проводником при охлаждении во внешнем магнитном поле, сохраняет в себе магнитное поле после выключения внешнего магнитного поля (в);
сверхпроводник, охлаждаемый в магнитном поле, после перехода в сверхпроводящее состояние выталкивает из своего объема внешнее магнитное поле – эффект Мейснера – Оксенфельда (г)