Содержание
- 2. СОХРАНЯЮЩИЕЕСЯ ВЕЛИЧИНЫ
- 3. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И РАБОТА
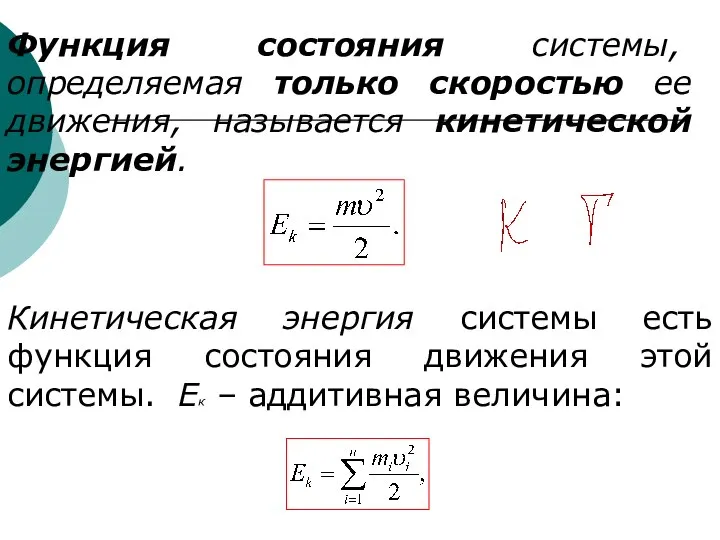
- 5. Функция состояния системы, определяемая только скоростью ее движения, называется кинетической энергией. Кинетическая энергия системы есть функция
- 6. отсюда Связь кинетической энергии с импульсом p. Т.к.
- 7. Связь кинетической энергии с работой. Если постоянная сила действует на тело, то оно будет двигаться в
- 8. Следовательно, работа силы приложенной к телу на пути r численно равна изменению кинетической энергии этого тела:
- 9. Мощность есть работа, совершаемая в единицу времени. Мгновенная мощность или Средняя мощность Скорость совершения работы (передачи
- 10. Консервативные силы и системы Кроме контактных взаимодействий, наблюдаются взаимодействия между телами, удаленными друг от друга. Подобное
- 11. Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и
- 12. Изменение направления движения на противоположное – вызывает изменение знака работы консервативных сил. Отсюда следует, что работа
- 13. Если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна. Консервативные силы: сила тяжести, электростатические
- 14. Потенциальная энергия Если на систему материальных тел действуют консервативные силы, то можно ввести понятие потенциальной энергии.
- 15. Потенциальная энергия U (х, у, z) – функция состояния системы, зависящая только от координат всех тел
- 16. Потенциальная энергия при гравитационном взаимодействии Работа тела при падении Или Условились считать, что на поверхности земли
- 17. Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга,
- 18. Потенциальная энергия упругой деформации (пружины) Найдём работу, совершаемую при деформации упругой пружины. Сила упругости Сила непостоянна,
- 19. Т.е. Примем: тогда
- 20. Закон сохранения механической энергии Закон сохранения сводит воедино результаты, полученные нами раньше. В сороковых годах девятнадцатого
- 21. Для консервативной системы частиц можно найти полную энергию системы: Для механической энергии закон сохранения звучит так:
- 22. Для замкнутой системы, т.е. для системы на которую не действуют внешние силы, можно записать: т.е. полная
- 23. Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия системы не сохраняется – частично
- 24. Закон сохранения импульса
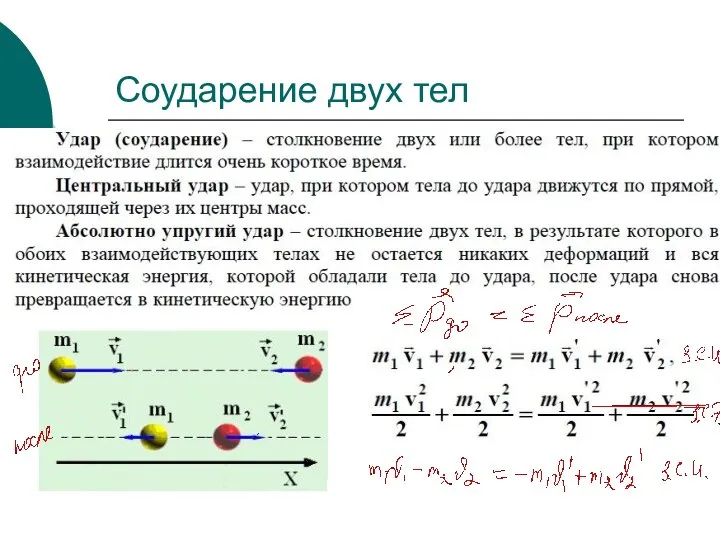
- 25. Соударение двух тел
- 28. Скачать презентацию
















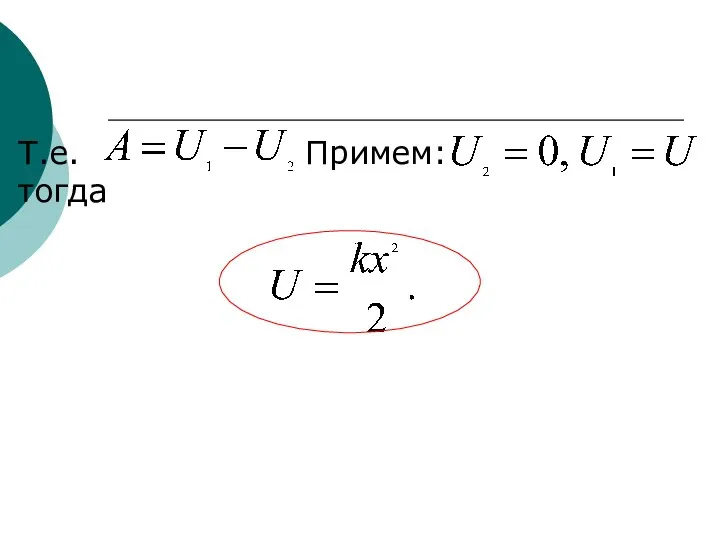






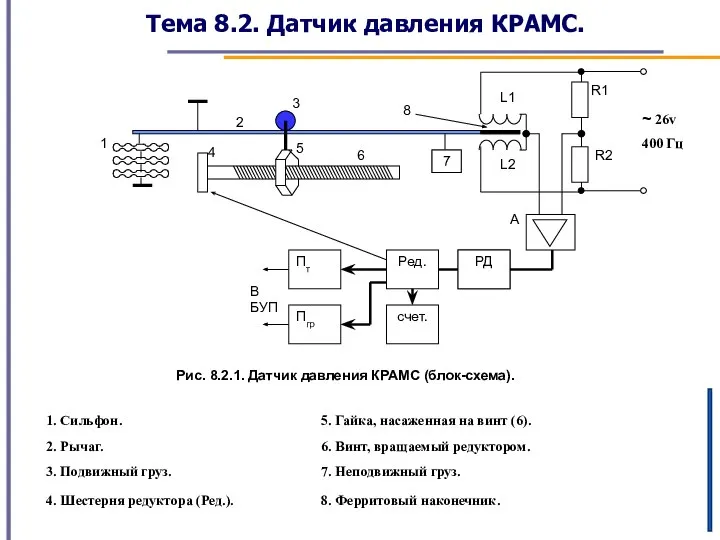 Датчик давления КРАМС
Датчик давления КРАМС Электрические свойства веществ - классификация
Электрические свойства веществ - классификация Трение в живой природе
Трение в живой природе Силы в механике. Силы тяготения. Силы упругости. Силы трения
Силы в механике. Силы тяготения. Силы упругости. Силы трения Презентация на тему Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции
Презентация на тему Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции  Электрические схемы. Элементы и параметры электрических цепей
Электрические схемы. Элементы и параметры электрических цепей Действие магнитного поля на проводник с током. Сила Ампера
Действие магнитного поля на проводник с током. Сила Ампера рем. техн. обор-ия
рем. техн. обор-ия Испарение. Насыщенный и ненасыщенный пар. Поглощение энергии при испарении жидкости и выделение ее при конденсации
Испарение. Насыщенный и ненасыщенный пар. Поглощение энергии при испарении жидкости и выделение ее при конденсации Вынужденные колебания
Вынужденные колебания Закон Ома для участка цепи
Закон Ома для участка цепи Механическая работа. 7 класс
Механическая работа. 7 класс Исследование фазового равновесия
Исследование фазового равновесия Радиоактивность. Модели атомов
Радиоактивность. Модели атомов Давление. Единицы давления
Давление. Единицы давления Колебания. Общие понятия
Колебания. Общие понятия Регулярные вариации низкочастотных акустических полей
Регулярные вариации низкочастотных акустических полей Слесарные операции
Слесарные операции Механическое движение. Положение тела в пространстве
Механическое движение. Положение тела в пространстве Квалификационные билеты. Билет № 1
Квалификационные билеты. Билет № 1 Тест по физике в форме ЕГЭ, часть А
Тест по физике в форме ЕГЭ, часть А Свободное падение тел (9 класс)
Свободное падение тел (9 класс) Экзаменационные вопросы по ФЯР
Экзаменационные вопросы по ФЯР Двигатели
Двигатели Теория колебаний
Теория колебаний Топология квантовой физики
Топология квантовой физики Электромагнитные колебания
Электромагнитные колебания Потенциальная энергия заряженного тела в однородном электростатическом поле
Потенциальная энергия заряженного тела в однородном электростатическом поле