Слайд 2Образец оформления выполнения задания:
17.03.2021
Фамилия, имя студента
Тема: «Пара сил и момент силы

относительно точки»
Ответы на контрольные вопросы:
1.
2.
3.
Слайд 3Лекция
Пара сил и момент силы относительно точки

Слайд 4Парой сил называется система двух сил, равных по модулю, параллельных и направленных

в разные стороны.
Слайд 5Рассмотрим систему сил (F, F1), образующих пару.
Пара сил вызывает вращение тела, и

ее действие на тело оценивается моментом.
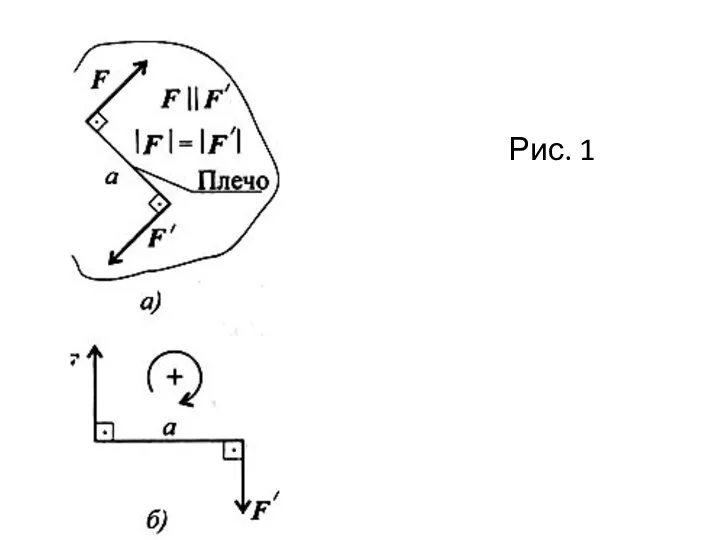
Силы, входящие в пару, не уравновешиваются, т. к. они приложены к двум точкам (рис. 1). Их действие на тело не может быть заменено одной силой (равнодействующей).
Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил (плечо пары).
Момент считают положительным, если пара вращает тело по часовой стрелке (рис. 1 б): M(F; F') = Fa; М > 0.
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.
Слайд 7Свойства пар (без доказательств):
Пару сил можно перемещать в плоскости ее действия.
Эквивалентность пар.

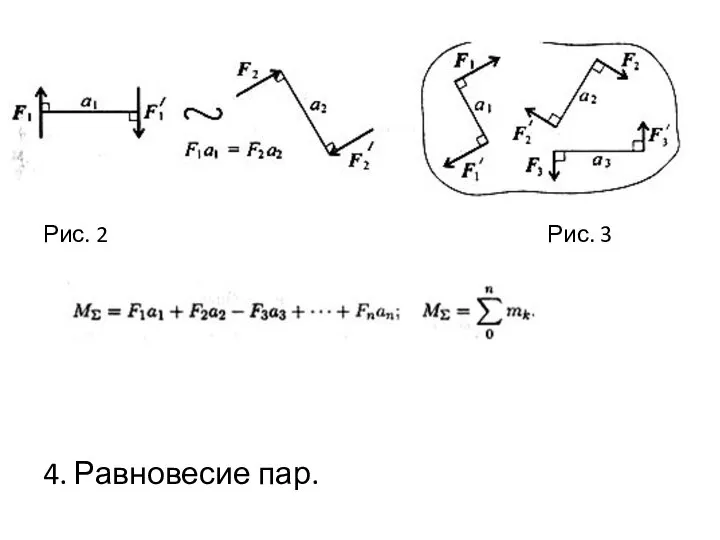
Две пары, моменты которых равны, (рис. 2) эквивалентны (действие их на тело аналогично).
Сложение пар сил. Систему пар сил можно заменить равнодействующей парой.
Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 3):
Слайд 84. Равновесие пар.
Рис. 2 Рис. 3
Слайд 9Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы

равнялась нулю
Слайд 10Момент силы относительно точки
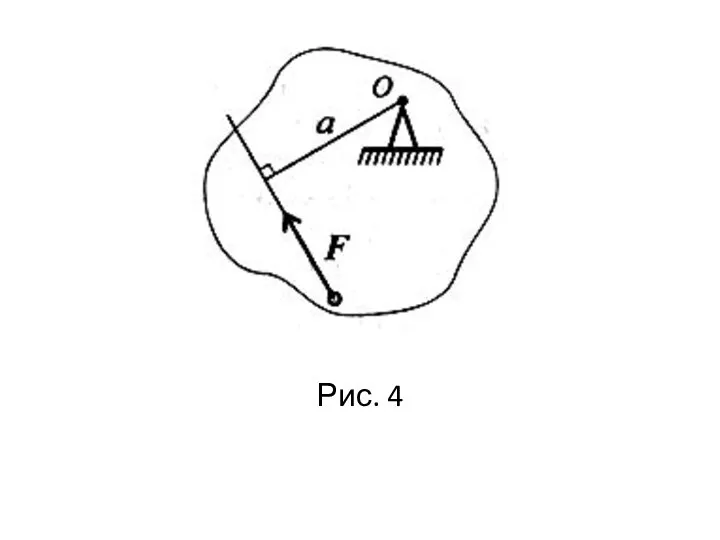
Сила, не проходящая через точку крепления тела, вызывает вращение

тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению модуля силы на расстояние от точки до линий действия силы.
Перпендикуляр, опущенный из точки на линию действия силы (рис. 4), называется плечом силы.
Слайд 12Обозначение момента Mo(F) или mО(F);
MО(F) = Fa.
Единица измерения [mО(F)] = Н*м.
Момент
![Обозначение момента Mo(F) или mО(F); MО(F) = Fa. Единица измерения [mО(F)] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1126880/slide-11.jpg)
считается положительным, если сила разворачивает тело по часовой стрелке.
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку, т. к. в этом случае расстояние от точки до силы равно нулю.








![Обозначение момента Mo(F) или mО(F); MО(F) = Fa. Единица измерения [mО(F)] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1126880/slide-11.jpg)
 Основи термодинаміки
Основи термодинаміки Презентация на тему Физика вокруг нас
Презентация на тему Физика вокруг нас  Классификация химических, физических и механических свойств порошка
Классификация химических, физических и механических свойств порошка Электрическое поле
Электрическое поле Разгон
Разгон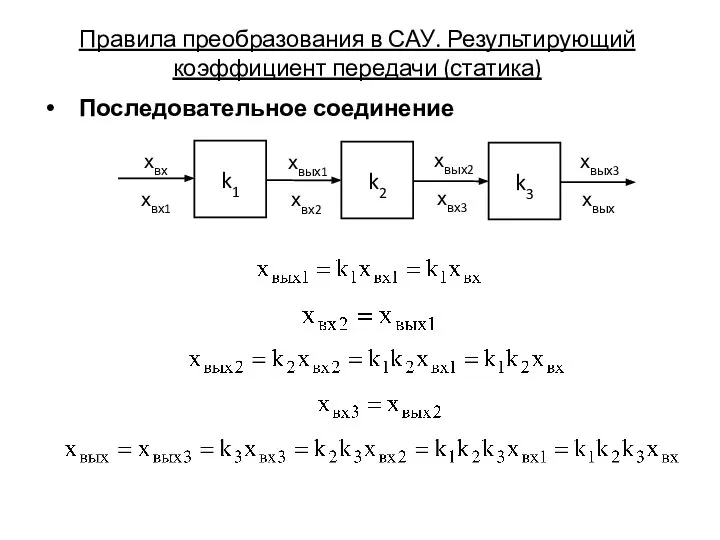 Правила преобразования в САУ. Результирующий коэффициент передачи (статика)
Правила преобразования в САУ. Результирующий коэффициент передачи (статика) Электрический заряд
Электрический заряд Определение коэффициента поверхностного натяжения жидкости методом капиллярных явлений и методом отрыва капель
Определение коэффициента поверхностного натяжения жидкости методом капиллярных явлений и методом отрыва капель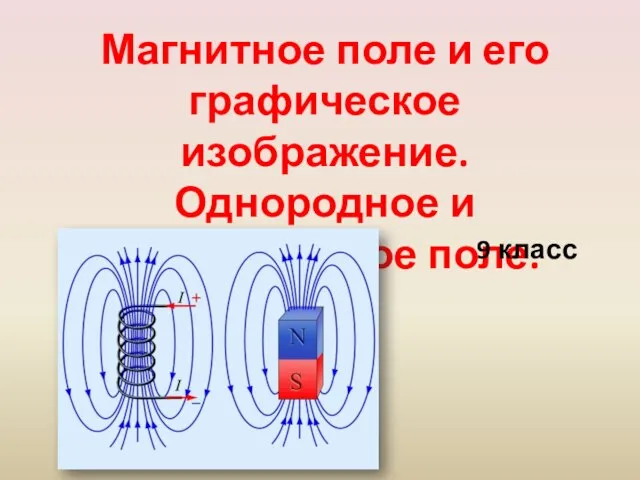 Магнитное поле и его графическое изображение. Однородное и неоднородное поле
Магнитное поле и его графическое изображение. Однородное и неоднородное поле Аккумулирование энергии
Аккумулирование энергии Презентация на тему Изобретатель радио – А.С. Попов
Презентация на тему Изобретатель радио – А.С. Попов  Электрический ток в вакууме
Электрический ток в вакууме Рух тіла під дією кількох сил
Рух тіла під дією кількох сил Проводники с током в магнитном поле. Теорема Гаусса для магнитного поля
Проводники с током в магнитном поле. Теорема Гаусса для магнитного поля Расширение воздуха при нагревании
Расширение воздуха при нагревании Полный факторный эксперимент
Полный факторный эксперимент Газовые законы
Газовые законы Уход за швейной машиной
Уход за швейной машиной Законы Ньютона
Законы Ньютона Воздухоплавание
Воздухоплавание Гидростатическое давление в точке. Тема 1
Гидростатическое давление в точке. Тема 1 Кинематика. Средняя скорость
Кинематика. Средняя скорость Однофазные цепи
Однофазные цепи Experimental methods for studies of ion – molecule reaktions and of ion – electron rekombination
Experimental methods for studies of ion – molecule reaktions and of ion – electron rekombination Квантовая криптография
Квантовая криптография Линзы. Виды линз
Линзы. Виды линз Анализаторы ситовые
Анализаторы ситовые Архитектурно-строительная акустика
Архитектурно-строительная акустика