Содержание
- 2. Преобразование Фурье(ПФ) Это преобразование позволяет получить амплитуду от частоты из амплитуды от времени и наоборот. Проблемы
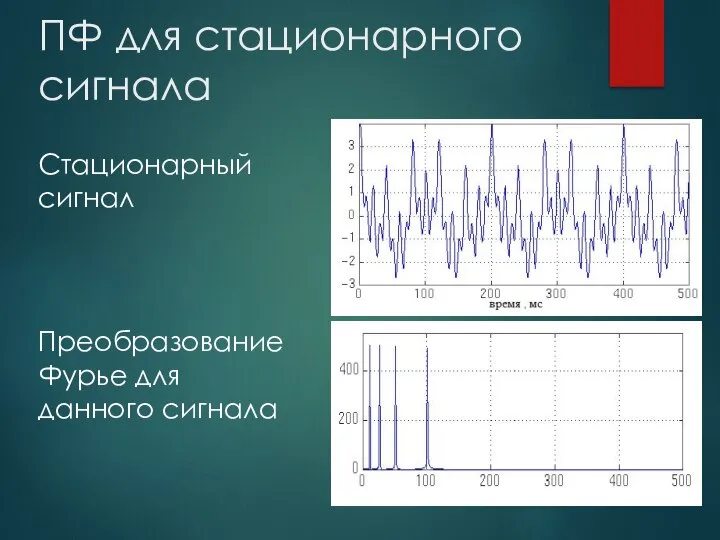
- 3. ПФ для стационарного сигнала Стационарный сигнал Преобразование Фурье для данного сигнала
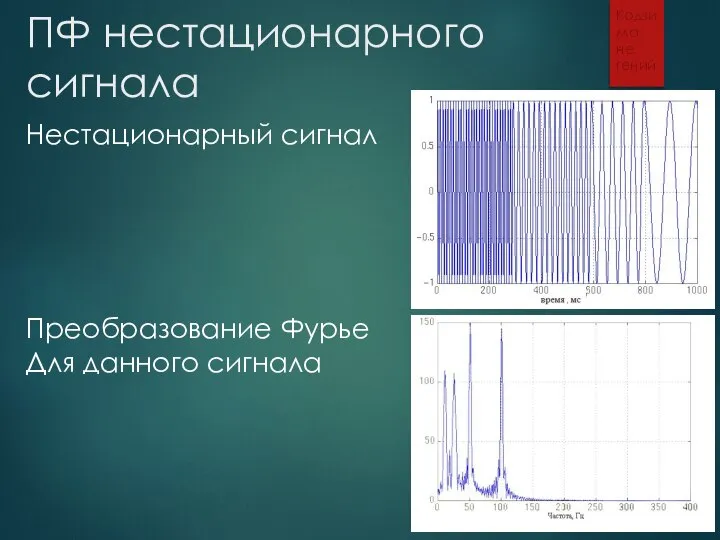
- 4. ПФ нестационарного сигнала Кодзима не гений Нестационарный сигнал Преобразование Фурье Для данного сигнала
- 5. Оконное ПФ(ОПФ) Ранее для нестационарных сигналов использовалось ОПФ. Суть в том, что мы берем промежуток времени
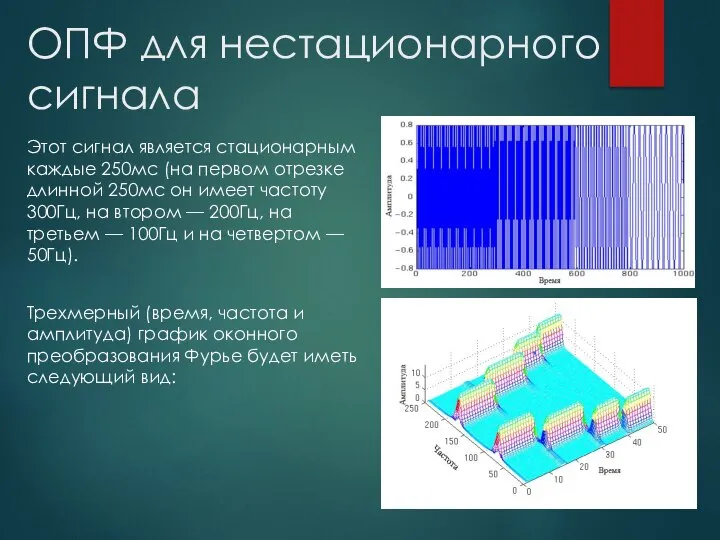
- 6. ОПФ для нестационарного сигнала Этот сигнал является стационарным каждые 250мс (на первом отрезке длинной 250мс он
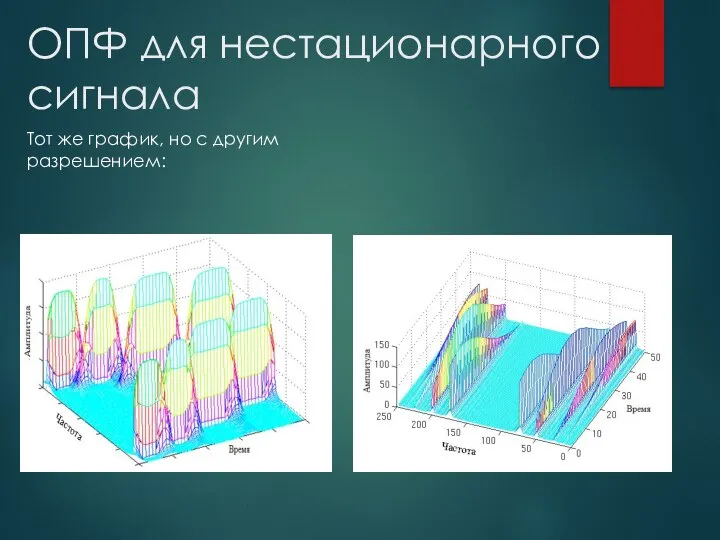
- 7. ОПФ для нестационарного сигнала Тот же график, но с другим разрешением:
- 8. Вейвлет-преобразование τ (тау) - сдвиг, s – масштаб(видно из формулы) ψ – материнский вейвлет Материнских вейвлетов
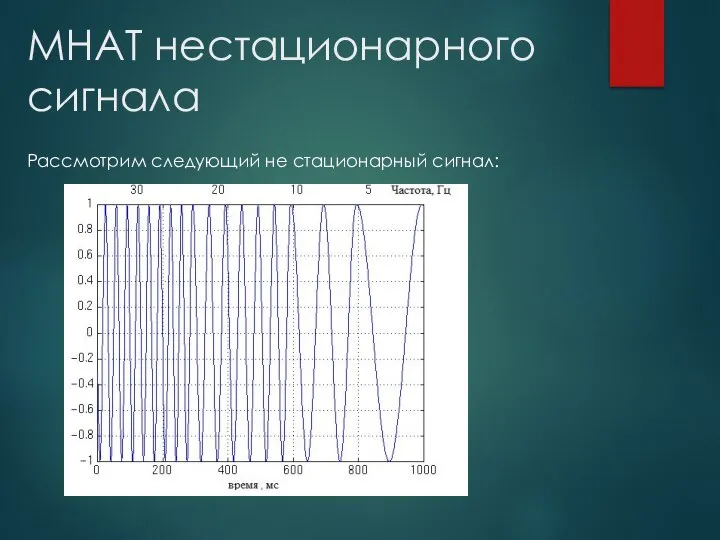
- 9. MHAT нестационарного сигнала Рассмотрим следующий не стационарный сигнал:
- 11. Скачать презентацию



 Магнитное поле Земли
Магнитное поле Земли Определение коэффициента поверхностного натяжения жидкости методом капиллярных явлений и методом отрыва капель
Определение коэффициента поверхностного натяжения жидкости методом капиллярных явлений и методом отрыва капель Материально-техническое обеспечение
Материально-техническое обеспечение Электричество и магнетизм. Лекция 09
Электричество и магнетизм. Лекция 09 Познавательнотематическое развлечение Течёт река…
Познавательнотематическое развлечение Течёт река…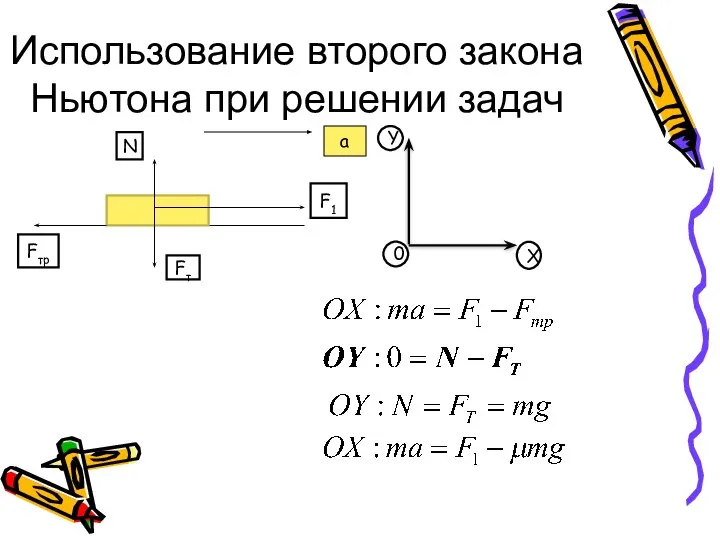 Использование второго закона Ньютона при решении задач
Использование второго закона Ньютона при решении задач Закон Архимеда
Закон Архимеда Магнитное поле. Основные уравнения магнитостатики в вакууме. Лекция № 6
Магнитное поле. Основные уравнения магнитостатики в вакууме. Лекция № 6 Наука физика
Наука физика Сила тока. Измерение силы тока
Сила тока. Измерение силы тока Физика сварочных процессов
Физика сварочных процессов Стандартная атмосфера. Лекция 4
Стандартная атмосфера. Лекция 4 Физическое лото (викторина 8 класс)
Физическое лото (викторина 8 класс) opredelenie_koordinaty_dvizh_tela
opredelenie_koordinaty_dvizh_tela Магнитное поле электрического тока
Магнитное поле электрического тока Электромагнитные волны
Электромагнитные волны 680-сильная Toyota Camry
680-сильная Toyota Camry Сила скрученной резины. (2 класс)
Сила скрученной резины. (2 класс) Презентация Механика Лекция 4
Презентация Механика Лекция 4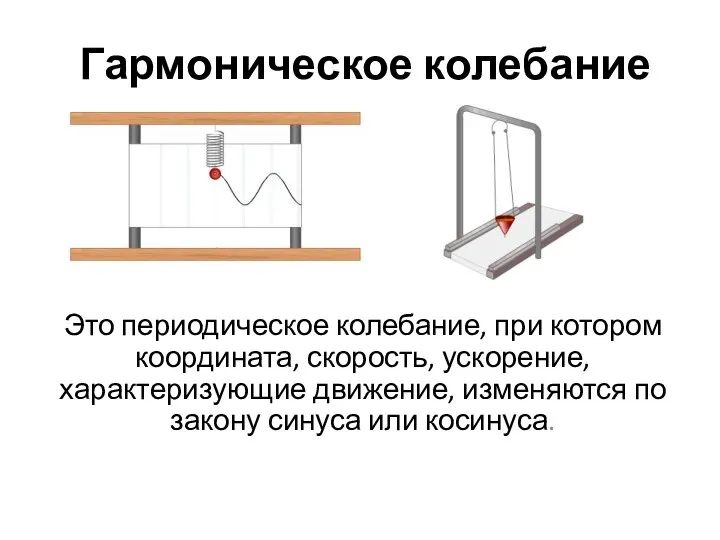 Гармоническое колебание
Гармоническое колебание Параллельный перенос сил. Связи и их реакции. Уравнения равновесия
Параллельный перенос сил. Связи и их реакции. Уравнения равновесия Строение атомного ядра, радиоактивность
Строение атомного ядра, радиоактивность Организация работ на участке регулировки углов установки колес автомобилей в ООО Лаки Моторс Сервис
Организация работ на участке регулировки углов установки колес автомобилей в ООО Лаки Моторс Сервис Презентация на тему Идеальный газ в МКТ
Презентация на тему Идеальный газ в МКТ  Конструктивная классификация (лекция №1)
Конструктивная классификация (лекция №1) Квантовая криптография
Квантовая криптография Вибрация подшипников качения
Вибрация подшипников качения Презентация на тему Виды излучений
Презентация на тему Виды излучений