Переходные процессы в линейных электрических цепях

ПЛАН
Понятие переходного процесса.
Законы коммутации.
Независимые и зависимые начальные условия.
Характеристическое уравнение электрической цепи.
Классический метод расчета переходных процессов.
Переходные процессы в RL-цепях постоянного тока.
Заряд и разряд конденсатора.

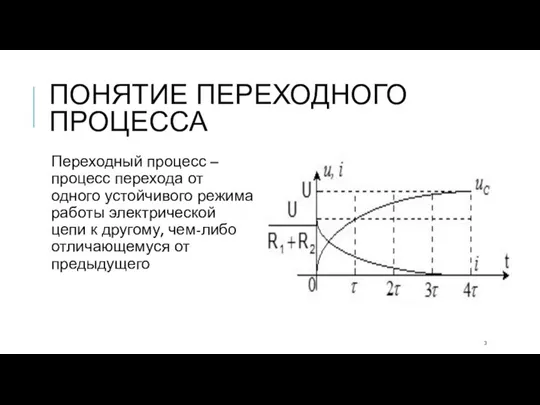
ПОНЯТИЕ ПЕРЕХОДНОГО ПРОЦЕССА
Переходный процесс – процесс перехода от одного устойчивого режима работы электрической цепи к другому, чем-либо отличающемуся от предыдущего

ПОНЯТИЕ ПЕРЕХОДНОГО ПРОЦЕССА
Возникает вследствие коммутации:
включения или отключения пассивных или активных ветвей,
коротких замыканий отдельных участков,
различного рода переключений,
внезапного изменения параметров и т.д.
Заканчивается спустя некоторое время после коммутации

ПОНЯТИЕ ПЕРЕХОДНОГО ПРОЦЕССА
Коммутация в переходных процессах — мгновенное изменение параметров электрической цепи
Коммутация — процессы, происходящие в первый момент времени после переключения в электрических цепях при замыканиях и размыканиях различных участков цепи

ПОНЯТИЕ ПЕРЕХОДНОГО ПРОЦЕССА
Начало отсчета времени переходного процесса t=0 начинается с момента коммутации
Момент времени непосредственно перед коммутацией t=0-
Момент времени сразу после коммутации - t=0+

ПОНЯТИЕ ПЕРЕХОДНОГО ПРОЦЕССА
Цель расчета – в определении законов изменения токов и напряжений во время коммутации

ЗАКОНЫ КОММУТАЦИИ.
ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
Ток через индуктивность непосредственно до коммутации равен току через ту же индуктивность непосредственно после коммутации
Ток на индуктивности не может изменяться скачком

ЗАКОНЫ КОММУТАЦИИ.
ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
По второму закону Кирхгофа:

ЗАКОНЫ КОММУТАЦИИ.
ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
Пусть ток во время переходного процесса изменится скачком, т.е. за время ток изменится на конечную величину
E – конечная величина, следовательно, не соблюдается II закон Кирхгофа, и предположение о том, что ток, протекающий через индуктивность, может измениться скачком, неверно

ЗАКОНЫ КОММУТАЦИИ.
ВТОРОЙ ЗАКОН КОММУТАЦИИ
Напряжение на емкости непосредственно до коммутации равно напряжению на той же емкости непосредственно после коммутации,
Напряжение на емкости не может измениться скачком

ЗАКОНЫ КОММУТАЦИИ.
ВТОРОЙ ЗАКОН КОММУТАЦИИ
По второму закону Кирхгофа:

ЗАКОНЫ КОММУТАЦИИ.
ВТОРОЙ ЗАКОН КОММУТАЦИИ
Пусть во время переходного процесса падение напряжения на конденсаторе изменится скачком, т.е. за время напряжение изменится на конечную величину
E – конечная величина, следовательно, не соблюдается II закон Кирхгофа, и предположение о том, что падение напряжения на конденсаторе может измениться скачком, неверно

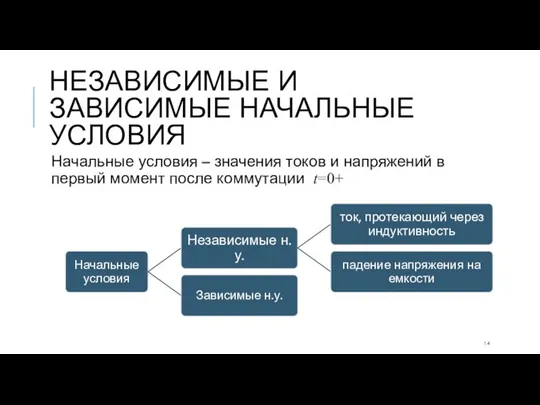
НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕ НАЧАЛЬНЫЕ УСЛОВИЯ
Начальные условия – значения токов и напряжений в первый момент после коммутации t=0+

НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕ НАЧАЛЬНЫЕ УСЛОВИЯ
Независимые начальные условия определяются из законов коммутации:
Зависимые начальные условия определяются из законов Кирхгофа и известных независимых начальных условий

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Расчет переходных процессов сводится к решению дифференциальных уравнений
Порядок дифференциального уравнения (степень характеристического уравнения) определяется числом независимых начальных условий в схеме после коммутации и не зависит от вида источников ЭДС в цепи

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Записывается входное сопротивление переменному току электрической цепи после коммутации
Заменяется в нем на р. Получается характеристическое уравнение
Находятся корни этого характеристического уравнения p. [p]=с-1.

ПРИМЕР
Составить характеристическое уравнение.
Найти его корни для электрической цепи

КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Для цепи после коммутации составить систему дифференциальных уравнений по I и II законам Кирхгофа.
Определить независимые начальные условия (uC и iL) из расчета режима цепи до коммутации с применением законов коммутации.
Записать искомые величины в виде суммы принужденных и свободных составляющих.
Найти принужденные составляющие, рассчитав установившийся режим цепи после коммутации.

КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Составить характеристическое уравнение и вычислить его корни.
В зависимости от вида корней характеристического уравнения записать свободные составляющие и искомые решения в общем виде.
Для определения постоянных интегрирования записать искомые величины, их производные и систему дифференциальных уравнений для момента t=0.
Подставить вычисленные постоянные интегрирования в искомые решения.
Построить графики изменения токов и напряжений во время переходного процесса.

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
Ключ замыкается.
Определить:
i(t), uR(t), uL(t)
По II закону Кирхгофа для послекоммутационной схемы:

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
По II закону Кирхгофа для послекоммутационной схемы:

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
i(t)=iсв+iпр
Для нахождения принужденной составляющей тока необходимо рассчитать установившийся режим после коммутации.
В установившемся режиме при протекании постоянного тока индуктивность - идеальный провод, падения напряжения на ней не происходит.

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
i(t)=iсв+iпр
Характеристическое уравнение:
Корень характеристического уравнения:

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
i(t)=iсв+iпр
Свободная составляющая:
где А – постоянный коэффициент, определяющийся из начальных условий

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
По первому закону коммутации

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RL-ЦЕПЯХ ПОСТОЯННОГО ТОКА
постоянная времени, которая определяет скорость изменения тока или напряжения во время переходного процесса
Доказано, что за время переходный процесс затухает и наступает установившийся режим

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
Ключ замыкается в положение 1 – конденсатор заряжается
Ключ замыкается в положение 2 – конденсатор разряжается

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(заряд конденсатора)
1. Ключ замыкается в положение 1 – конденсатор заряжается
Напряжение на конденсаторе до коммутации

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(заряд конденсатора)
По второму закону Кирхгофа

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(заряд конденсатора)
uC=uCпр+ uCсв
uCпр=U
uCсв=Aept
Характеристическое уравнение:
Корень характеристического уравнения

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(заряд конденсатора)
По II закону коммутации

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(заряд конденсатора)

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(разряд конденсатора)
2. Ключ замыкается в положение 2 – конденсатор разряжается
Конденсатор заряжен до напряжения, равного приложенному
uc(0-)=U

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(разряд конденсатора)
По II закону Кирхгофа для послекоммутационной схемы
Конденсатор заряжен до напряжения, равного приложенному
uc(0-)=U

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(разряд конденсатора)
По II закону Кирхгофа для послекоммутационной схемы
Конденсатор заряжен до напряжения, равного приложенному
uc(0-)=U

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(разряд конденсатора)
(в установившемся режиме после коммутации конденсатор полностью разряжается)

ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА
(разряд конденсатора)
Характеристическое уравнение
По II закону коммутации