Содержание
- 2. При действии света на вещество основное значение имеет электрическая составляющая электромагнитного поля световой волны, поскольку именно
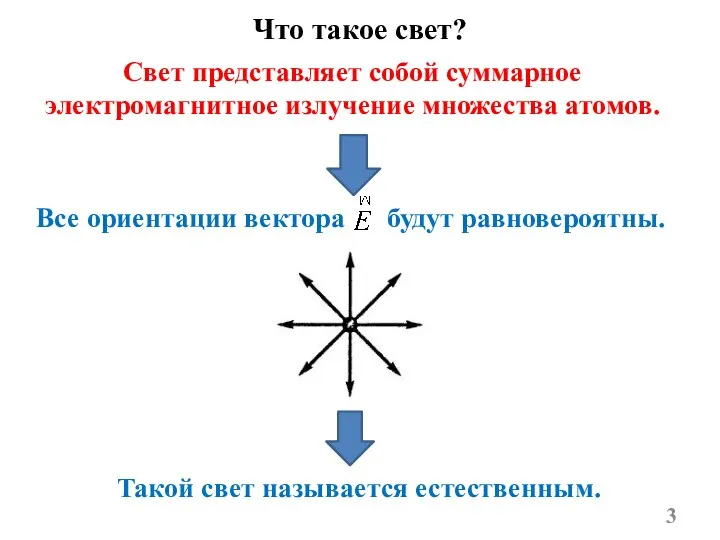
- 3. Что такое свет? Свет представляет собой суммарное электромагнитное излучение множества атомов. Все ориентации вектора будут равновероятны.
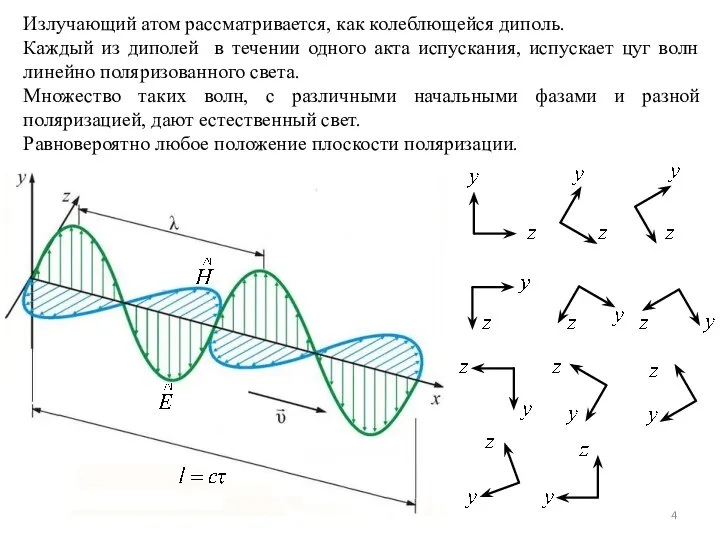
- 4. Излучающий атом рассматривается, как колеблющейся диполь. Каждый из диполей в течении одного акта испускания, испускает цуг
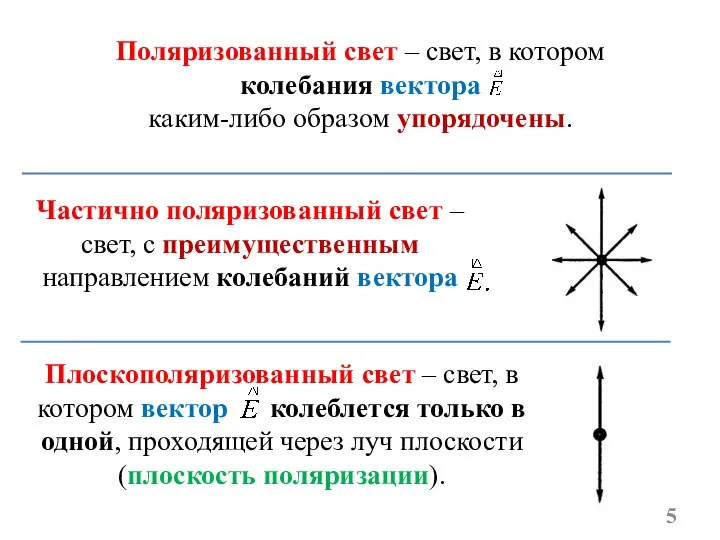
- 5. Поляризованный свет – свет, в котором колебания вектора каким-либо образом упорядочены. Частично поляризованный свет – свет,
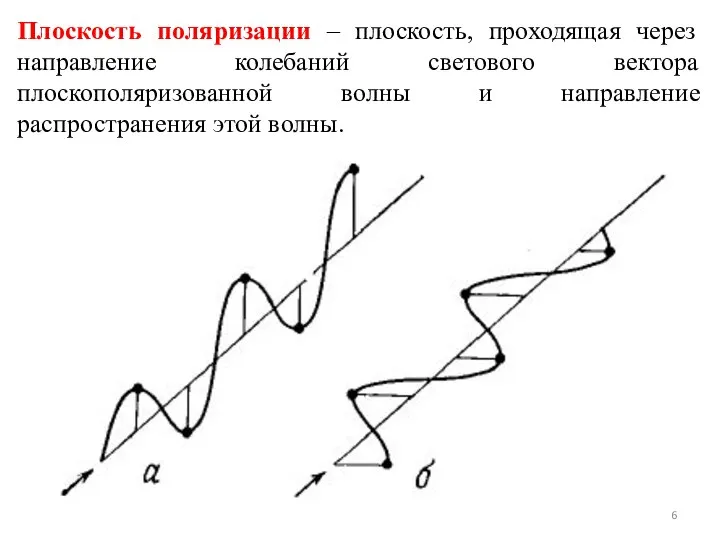
- 6. Плоскость поляризации – плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой
- 7. Степень поляризации – величина где Imax и Imin – соответственно максимальная и минимальная интенсивности света, пропускаемого
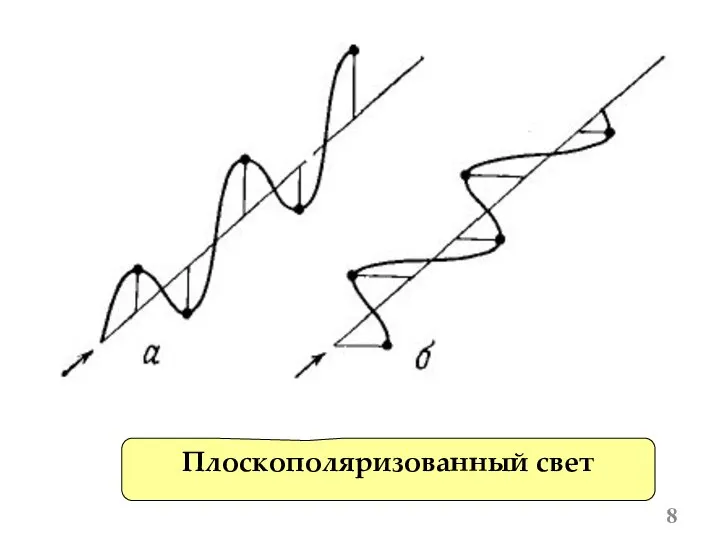
- 8. Плоскополяризованный свет
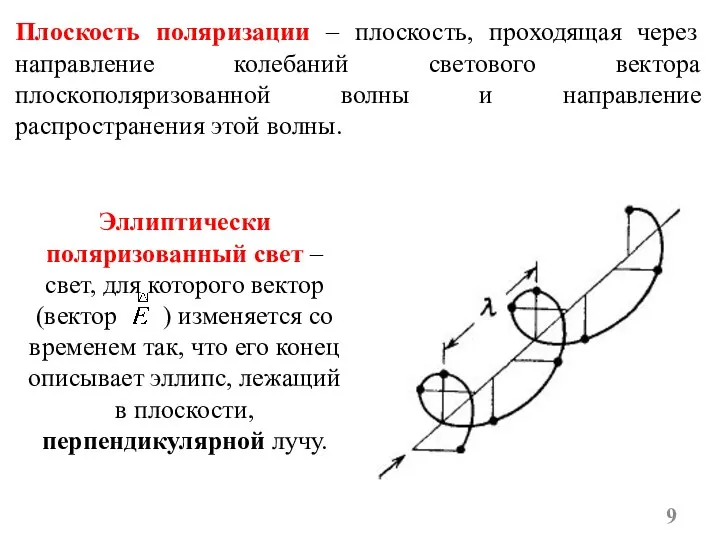
- 9. Плоскость поляризации – плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой
- 10. Вопрос. Как преобразовать естественный свет в плоскополяризованный? Ответ. Для этого используют так называемые поляризаторы – кристаллы
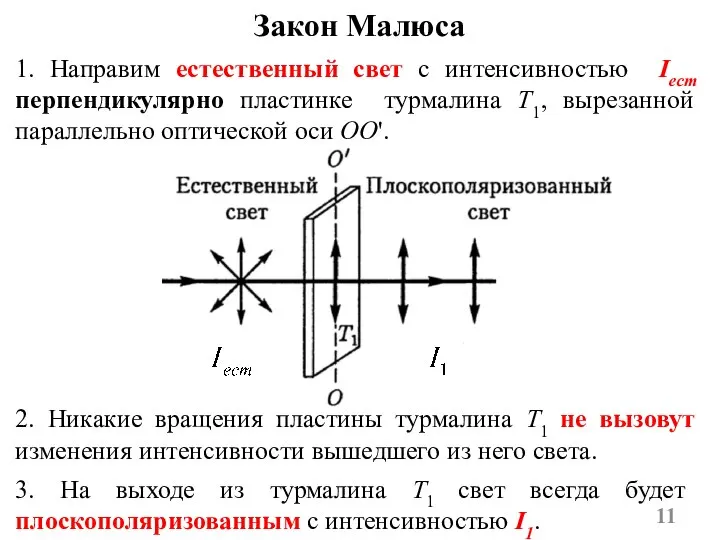
- 11. Закон Малюса 2. Никакие вращения пластины турмалина T1 не вызовут изменения интенсивности вышедшего из него света.
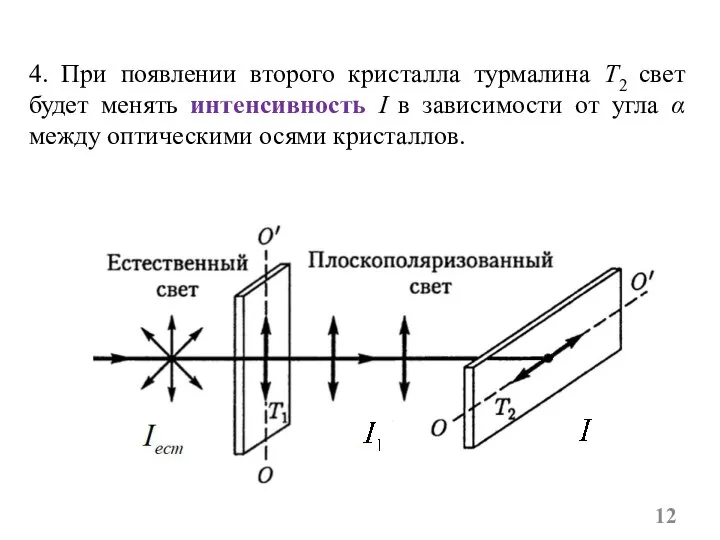
- 12. 4. При появлении второго кристалла турмалина T2 свет будет менять интенсивность I в зависимости от угла
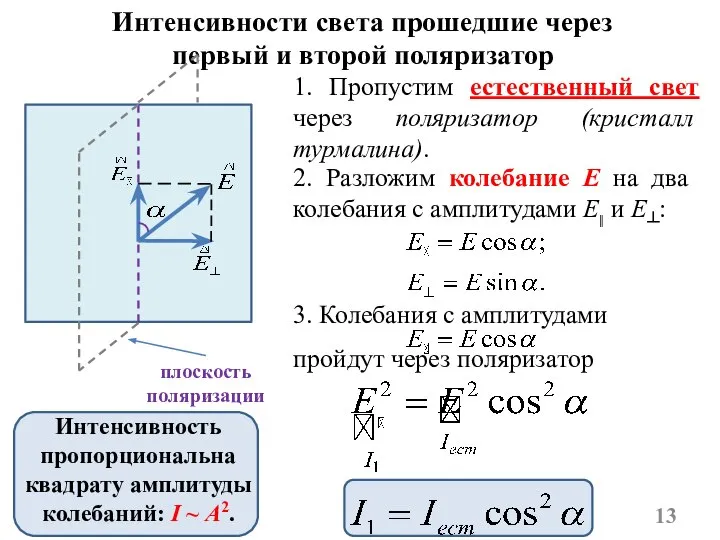
- 13. Интенсивности света прошедшие через первый и второй поляризатор 1. Пропустим естественный свет через поляризатор (кристалл турмалина).
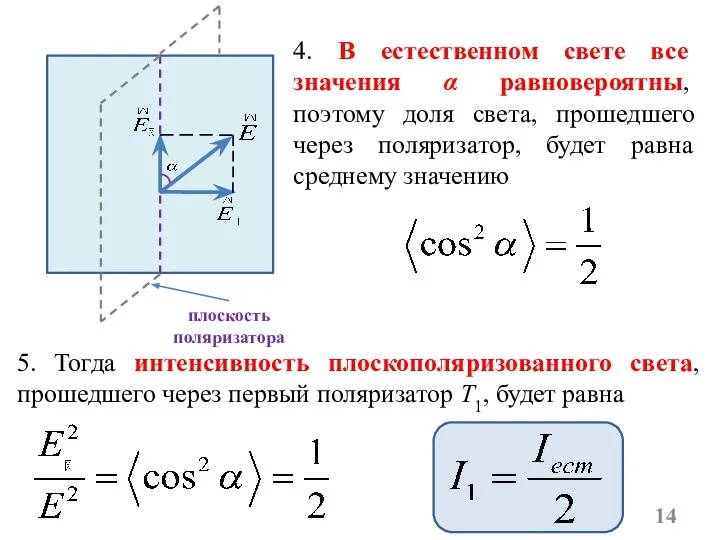
- 14. 4. В естественном свете все значения α равновероятны, поэтому доля света, прошедшего через поляризатор, будет равна
- 15. Вывод: При вращении поляризатора вокруг направления естественного луча интенсивность прошедшего света остаётся одной и той же,
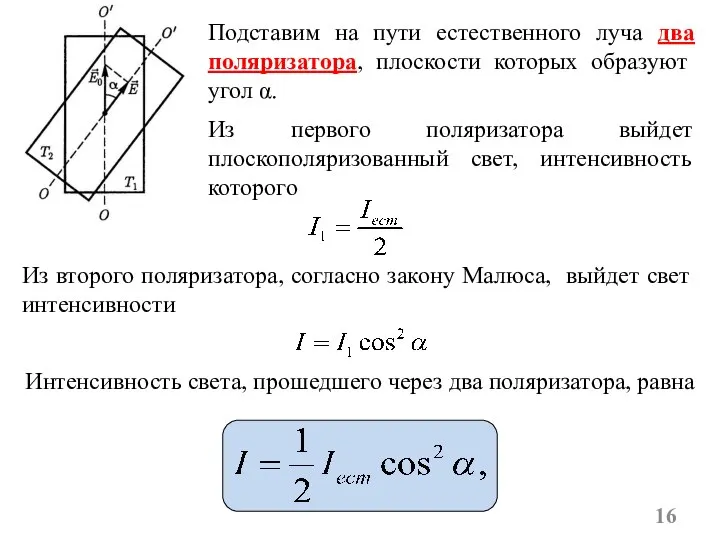
- 16. Подставим на пути естественного луча два поляризатора, плоскости которых образуют угол α. Из первого поляризатора выйдет
- 18. Закон Малюса Интенсивность I света, прошедшего через второй кристалл (турмалина) меняется в зависимости от угла α
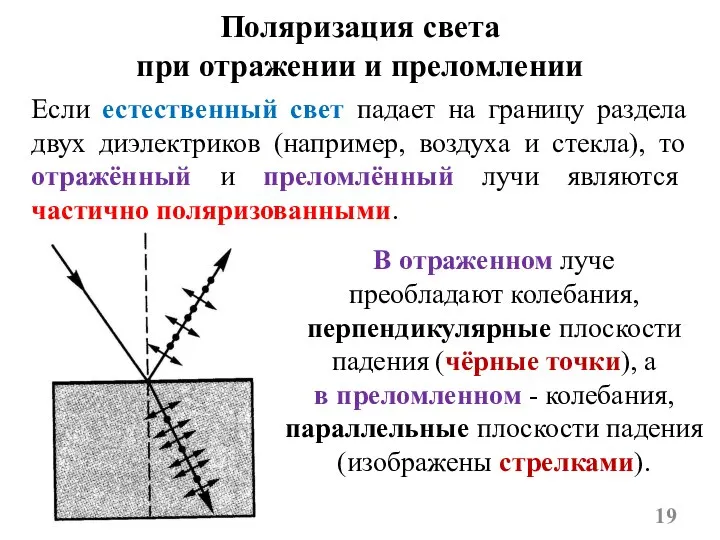
- 19. Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то отражённый и
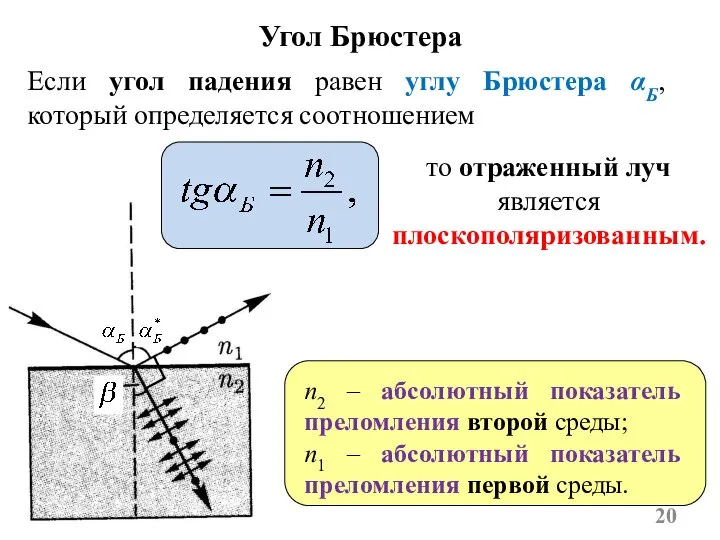
- 20. Если угол падения равен углу Брюстера αБ, который определяется соотношением то отраженный луч является плоскополяризованным. Угол
- 21. Преломленный луч в этом случае поляризуется максимально, но не полностью. При этом отраженный и преломленный лучи
- 22. Запишем закон преломления Приравняем
- 23. Отсюда По закону отражения Поэтому
- 24. Двойное лучепреломление Двойное лучепреломление – это способность прозрачных кристаллов (кроме оптически изотропных кристаллов кубической системы) раздваивать
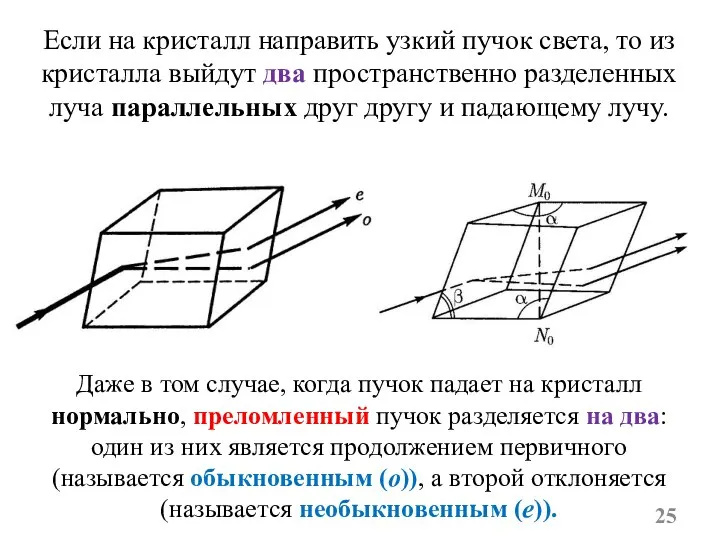
- 25. Если на кристалл направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча параллельных
- 26. Направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая двойного лучепреломления, называется оптической
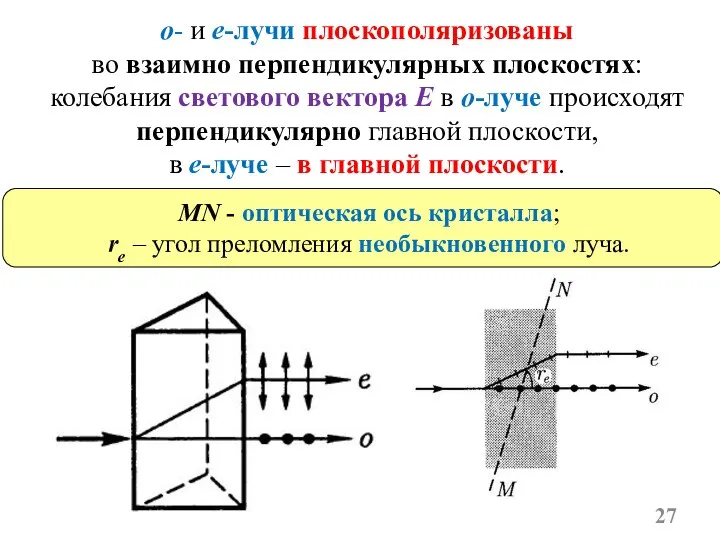
- 27. о- и е-лучи плоскополяризованы во взаимно перпендикулярных плоскостях: колебания светового вектора E в о-луче происходят перпендикулярно
- 28. о-луч распространяется по всем направлениям кристалла с одинаковой скоростью Показатель преломления n0 для него есть величина
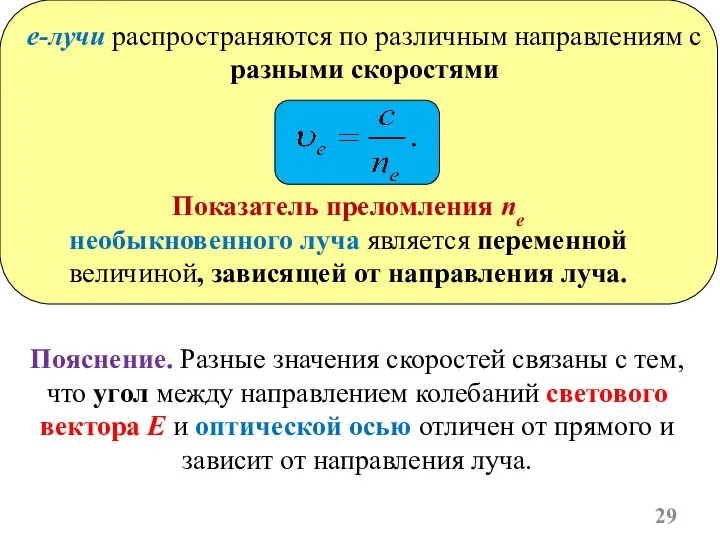
- 29. e-лучи распространяются по различным направлениям с разными скоростями Показатель преломления ne необыкновенного луча является переменной величиной,
- 30. Для луча, распространяющегося вдоль оптической оси, т.е. вдоль оптической оси существует только одна скорость распространения света.
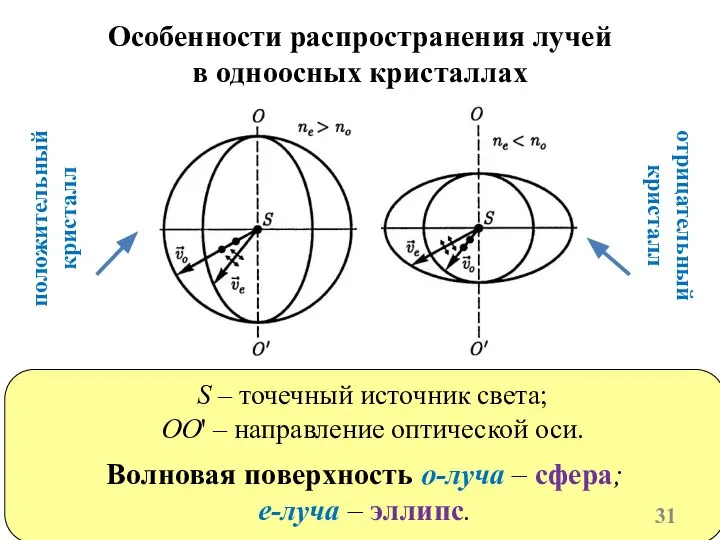
- 31. Особенности распространения лучей в одноосных кристаллах S – точечный источник света; OO' – направление оптической оси.
- 33. Скачать презентацию







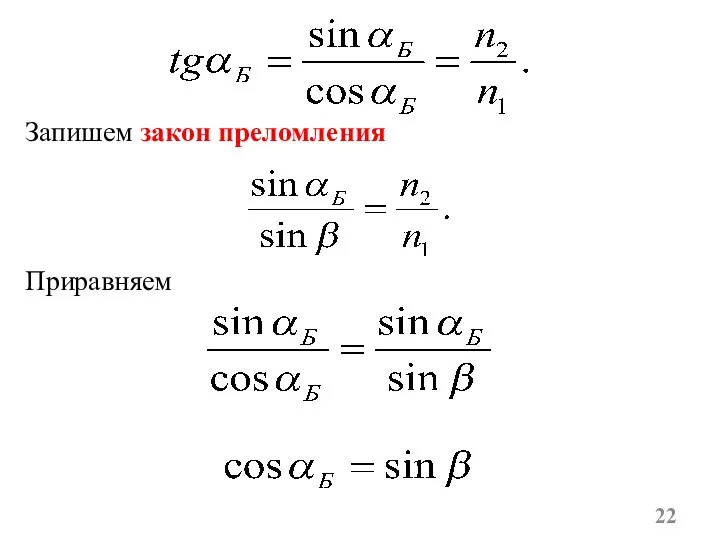





 Закон Архимеда
Закон Архимеда Напряженность электростатического поля
Напряженность электростатического поля Фотоны. Эффект Комптона
Фотоны. Эффект Комптона Кинематика вращательного движения
Кинематика вращательного движения Профилактика отечественного котла после 5 лет эксплуатации
Профилактика отечественного котла после 5 лет эксплуатации Диффузия. Роберт Броун
Диффузия. Роберт Броун Электронно-дырочный переход (p-n-переход)
Электронно-дырочный переход (p-n-переход) Презентация_Кинематика криволинейное движение (2)
Презентация_Кинематика криволинейное движение (2) Сокращенное наименование единиц СИ
Сокращенное наименование единиц СИ Необычные свойства обычной воды
Необычные свойства обычной воды Физика на рыбалке
Физика на рыбалке Устройство тракторов
Устройство тракторов Решение задач на закон Ома для однородного участка
Решение задач на закон Ома для однородного участка Поиск повреждений в магистральных кабелях связи
Поиск повреждений в магистральных кабелях связи Устройства ввода информации
Устройства ввода информации Звуковые волны
Звуковые волны Движение квазичастиц электронов в электрическом поле
Движение квазичастиц электронов в электрическом поле Презентация на тему Механические волны
Презентация на тему Механические волны  Радіолокація. Радіомовлення і телебачення. Супутникове телебачення. 11 клас
Радіолокація. Радіомовлення і телебачення. Супутникове телебачення. 11 клас Барометрическая формула. Распределение Больцмана
Барометрическая формула. Распределение Больцмана Задачи по физико-химической очистке воды
Задачи по физико-химической очистке воды 151c81f567f6a33917e4696ac6d03f7b
151c81f567f6a33917e4696ac6d03f7b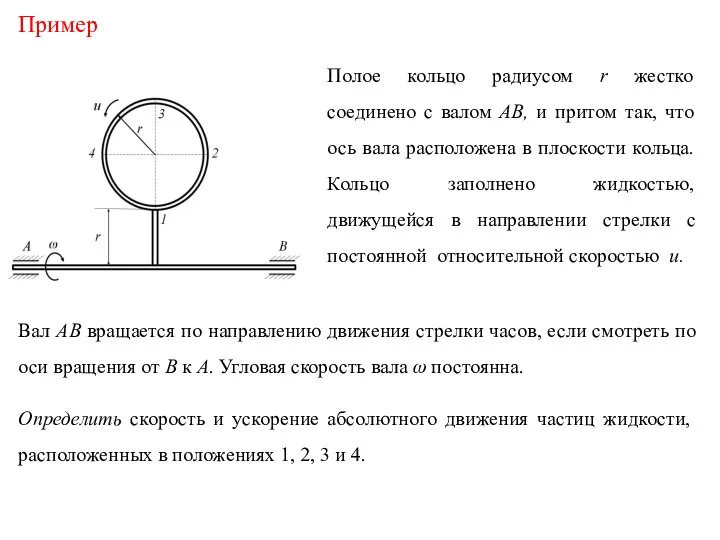 Скорость и ускорение абсолютного движения частиц жидкости
Скорость и ускорение абсолютного движения частиц жидкости Механическая работа. Единицы работы
Механическая работа. Единицы работы Квантовая физика, часть1
Квантовая физика, часть1 Линейный электрический погружной насос ООО ВТО Промышленные технологи
Линейный электрический погружной насос ООО ВТО Промышленные технологи Презентация на тему Физические величины
Презентация на тему Физические величины  Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью