Содержание
- 2. 1. Коэффициенты переноса и их зависимость от давления Сопоставим N = −D gradU или Уравнение Фика
- 3. Эта теория позволила установить, что внешнее сходство уравнений обусловлено общностью лежащих в их основе молекулярного механизма
- 4. Но это конечно не так. Все выше указанные коэффициенты связаны между собой и все выводы молекулярно
- 5. Рассмотрим зависимость коэффициента переноса от давления p. Так как скорость теплового движения молекул и не зависит
- 6. С увеличением p и ρ, повышается число молекул переносящих импульс из слоя в слой, но даёт
- 7. Молекулярное течение. Эффузия газов Молекулярное течение – течение газов в условиях вакуума. То есть, когда молекулы
- 8. Как при молекулярном течении, так и при эффузии количество протекающего в единицу времени газа обратно пропорционально
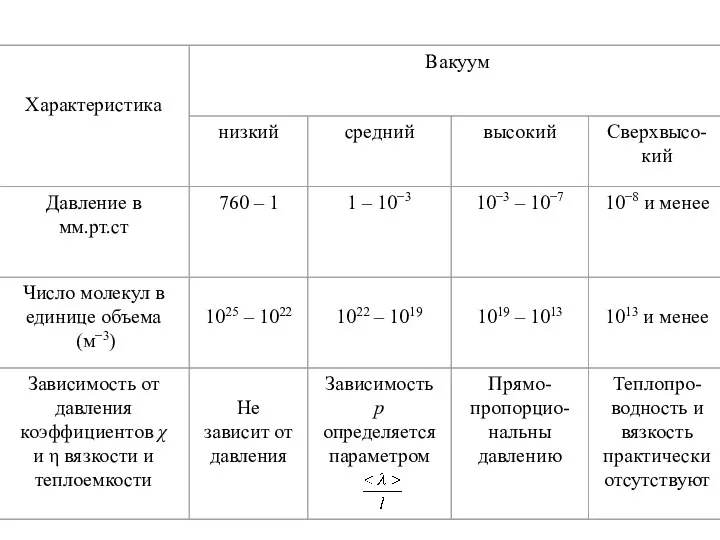
- 9. 2. Понятие о вакууме Газ называется разреженным (разреженный газ), если его плотность столь мала, что средняя
- 11. В состоянии высокого вакуума уменьшение плотности разреженного газа приводит к соответствующей убыли частиц без изменения 〈λ〉
- 12. Удельный тепловой поток в сильно разреженных газах пропорционален разности температур и плотности газа. Стационарное состояние разреженного
- 13. Если Т1 и Т2 – температуры газа в сосудах, то предыдущее условие стационарности можно переписать в
- 14. Вопросы создания вакуума имеют большое значение в технике, так как например, во многих современных электронных приборах
- 15. Лекция 22. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ВНУТРЕННЯЯ ЭНЕРГИЯ. РАБОТА И ТЕПЛОТА 1. Внутренняя энергия. Работа и теплота.
- 16. 1. Внутренняя энергия. Работа и теплота Наряду с механической энергией любое тело (или система) обладает внутренней
- 17. В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы изменить строение атома,
- 18. Изменение внутренней энергии U равно разности внутренней энергии в этих состояниях, независимо от пути, по которому
- 19. Например. Зимой вы бросили в снег горячий камень,
- 20. за счёт запаса потенциальной энергии (механическая) совершена работа по смятию снега, а за счёт запаса внутренней
- 21. Если же камень был холодный, т.е. температура камня равна температуре среды, то будет совершена только работа,
- 22. Опыт показывает, что во всех случаях превращение механической энергии в тепловую и обратно совершается всегда в
- 23. Учитывая правило знаков можно записать: U = Q–А (22.3) изменение внутренней энергии тела равно разности сообщаемой
- 24. Первое начало термодинамики Первое начало термодинамики есть закон сохранения энергии для макроскопических явлений, в которых одним
- 25. При контакте термодинамической системы с окружающей средой происходит обмен энергией. Возможны два различных способа передачи энергии
- 26. Затрачиваемая работа А может пойти на увеличение любого вида энергии, теплота Q непосредственно может пойти только
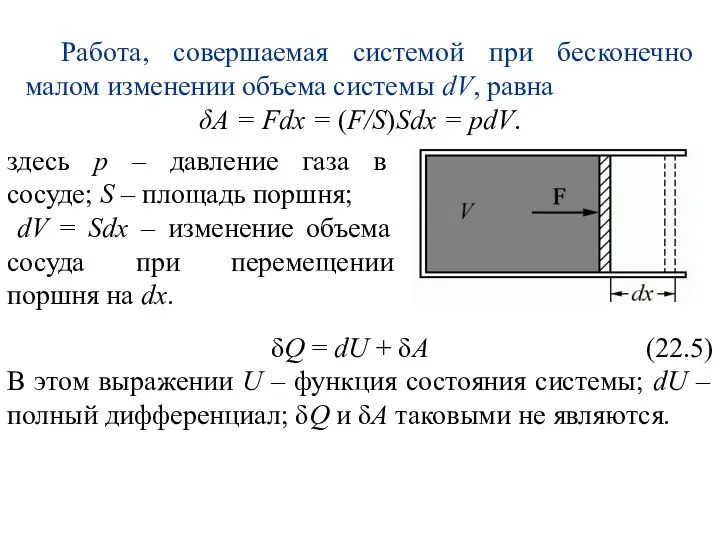
- 27. Работа, совершаемая системой при бесконечно малом изменении объема системы dV, равна δA = Fdx = (F/S)Sdx
- 28. В каждом состоянии система обладает определенным и только таким значением внутренней энергии, поэтому можно записать (22.6)
- 29. Величины δQ и δA бесконечно малы, но не являются полными дифференциалами, поскольку Q и A задаются
- 30. Из формулы δQ = dU + δA следует, что количество теплоты выражается в тех же единицах,
- 31. Если ΔU = 0, то согласно первому началу термо-динамики А = Q, т.е. !!!нельзя построить периодически
- 32. 2. Теплоёмкость идеального газа. Уравнение Майера Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела
- 33. Для газов удобно пользоваться молярной тепло-емкостью Сμ − количество теплоты необходимое для нагревания 1 моля газа
- 34. Если газ нагревать при постоян-ном объёме, то всё подводимое тепло идёт на нагревание газа, то есть
- 35. Итак, подводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Следовательно Q и
- 36. В общем случае (22.13) так как U может зависеть не только от температуры. Но в случае
- 37. Для произвольной массы идеального газа: (22.16) При изобарическом процессе кроме увеличения внутренней энергии происходит совершение работы
- 39. Скачать презентацию


































 Электрическое сопротивление. Удельное сопротивление
Электрическое сопротивление. Удельное сопротивление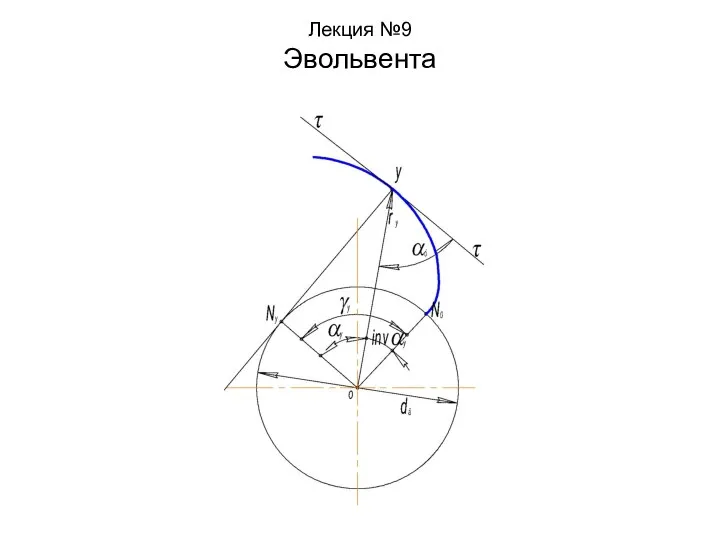 Эвольвента. Лекции 9
Эвольвента. Лекции 9 Параметры и виды передающих оптических модулей
Параметры и виды передающих оптических модулей Ультразвуковой контроль (УЗК). Методы и оборудование УЗД
Ультразвуковой контроль (УЗК). Методы и оборудование УЗД Механическое движение
Механическое движение Испарение. Насыщенный пар и его свойства. Влажность воздуха
Испарение. Насыщенный пар и его свойства. Влажность воздуха Теоретическая механика модуль 1. Раздел 2 – кинематика
Теоретическая механика модуль 1. Раздел 2 – кинематика Преобразования сигналов и Вейвлет-преобразование
Преобразования сигналов и Вейвлет-преобразование Ядерные силы. Дефект масс. Энергия связи
Ядерные силы. Дефект масс. Энергия связи Professional english for mechanics
Professional english for mechanics Развитие познавательного интереса к предмету физика
Развитие познавательного интереса к предмету физика Показатели надежности электроснабжения
Показатели надежности электроснабжения Оборудование для переработки каучука
Оборудование для переработки каучука Kinematika_tverdogo_tela_33__33__33
Kinematika_tverdogo_tela_33__33__33 Характеристика волн. Величины, характеризующие волну
Характеристика волн. Величины, характеризующие волну Методика организации и проведения лабораторного практикума по физике в современной школе
Методика организации и проведения лабораторного практикума по физике в современной школе Электрические цепи
Электрические цепи lek2 _кинем
lek2 _кинем Нелинейные СКВИД метаматериалы
Нелинейные СКВИД метаматериалы Строения атомов
Строения атомов Стенд для лабораторных работ Зубчатые передачи
Стенд для лабораторных работ Зубчатые передачи Какие бывают машины
Какие бывают машины Тепловые двигатели
Тепловые двигатели Игра для семиклассников Физика и мы
Игра для семиклассников Физика и мы Буровые машины для открытых горных пород. Лекция 8
Буровые машины для открытых горных пород. Лекция 8 масс-1
масс-1 Высота. Тембр и громкость звука
Высота. Тембр и громкость звука Touareg CR. Замена шаровой несущего рычага на автомобиле с пневмоподвеской
Touareg CR. Замена шаровой несущего рычага на автомобиле с пневмоподвеской