Гармонические колебания

Процесс удовлетворяющий условию:
называется гармоническими колебаниями.
Дифференциальное
уравнение
гармонических
колебаний.
Решением диф. уравнения является уравнение:
где:

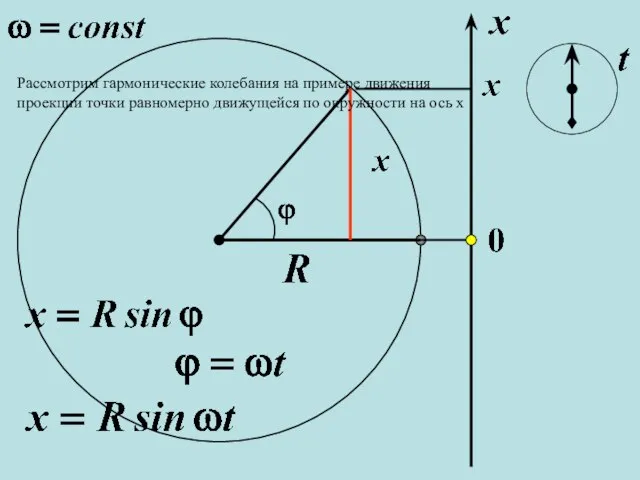
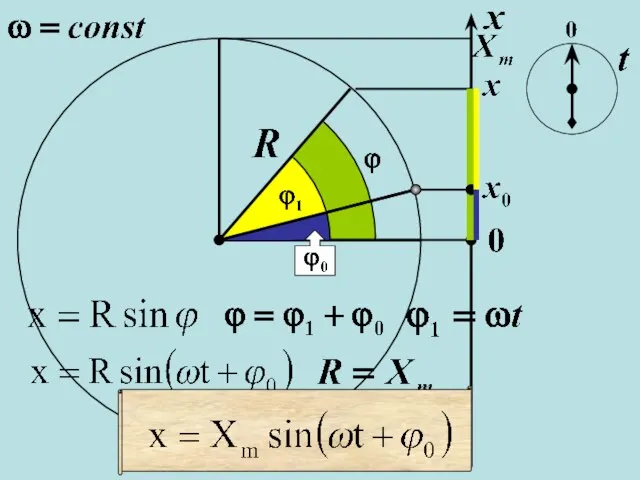
Рассмотрим гармонические колебания на примере движения
проекции точки равномерно движущейся по окружности на ось х

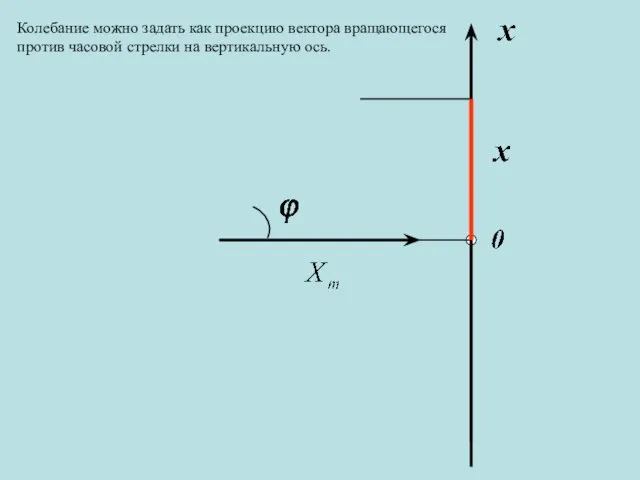
Колебание можно задать как проекцию вектора вращающегося
против часовой стрелки на вертикальную ось.

Гармонические осцилляторы.
Гармонические осцилляторы – это система колебания которой удовлетворяют
дифференциальному уравнению гармонических колебаний.
Свободными называются колебания системы предварительно выведенной из
положения равновесия и предоставленной самой себе.
Частота свободных не затухающих колебаний называется собственной частотой
колебаний системы.
Собственная частота

Рассмотрим пружинный маятник. ( система из абсолютно упругой пружины
и материальной точки).
Возвращающей силой является сила упругости.
или
или
Период колебаний пружинного маятника:

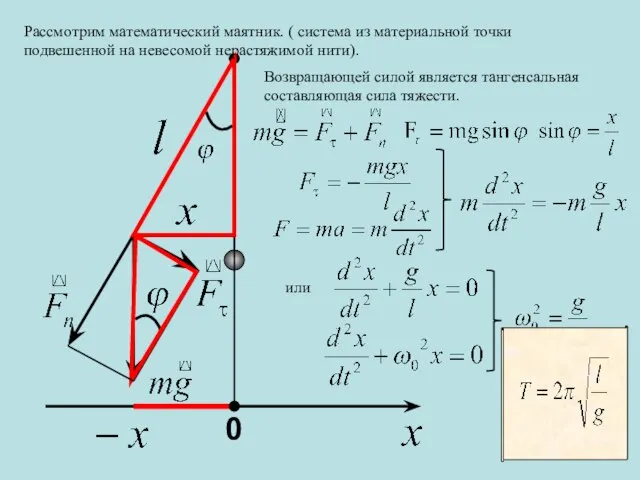
0
Рассмотрим математический маятник. ( система из материальной точки
подвешенной на невесомой нерастяжимой нити).
Возвращающей силой является тангенсальная
составляющая сила тяжести.
или

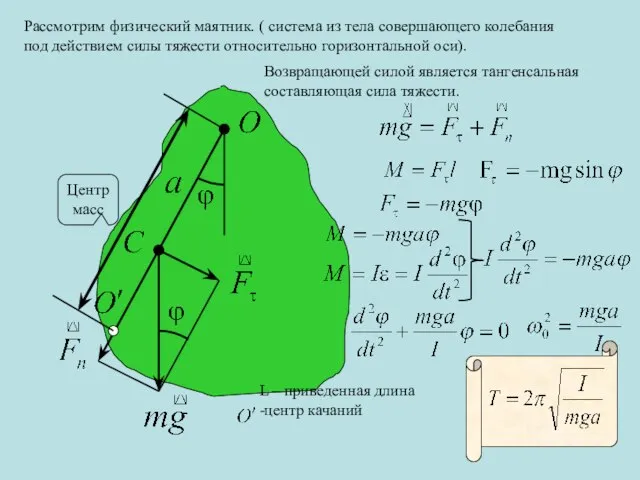
Рассмотрим физический маятник. ( система из тела совершающего колебания
под действием силы тяжести относительно горизонтальной оси).
Возвращающей силой является тангенсальная
составляющая сила тяжести.
Центр
масс