Содержание
- 2. Д.И.Менделеев Наука начинается с тех пор, как начинают измерять Портрет Менделеева в мантии профессора 1885 г
- 3. Меню 1. Что такое величина? 2. Какие величины называются физическими? 3. Что значит измерить физическую величину?
- 4. Всё, что может быть измерено, называется величиной 1.Что такое величина? Автор работы: Тертычная С.А. меню
- 5. Если величины характеризуют физические явления с количественной стороны, то они называются физическими величинами. 2. Какие величины
- 6. Измерения физических величин делятся на прямые и косвенные. Если измеряют саму исследуемую величину с помощью физических
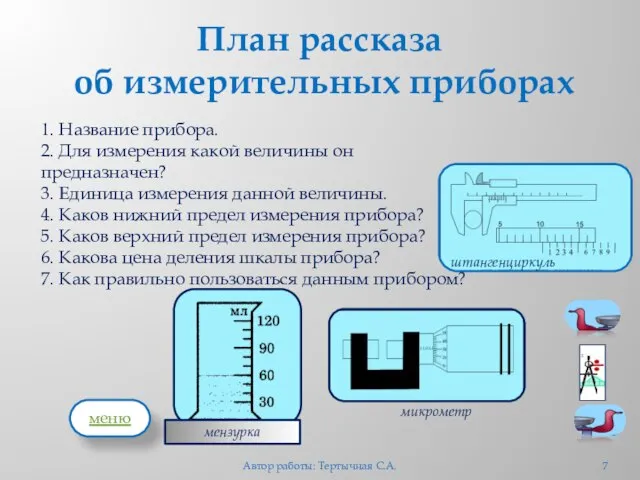
- 7. План рассказа об измерительных приборах 1. Название прибора. 2. Для измерения какой величины он предназначен? 3.
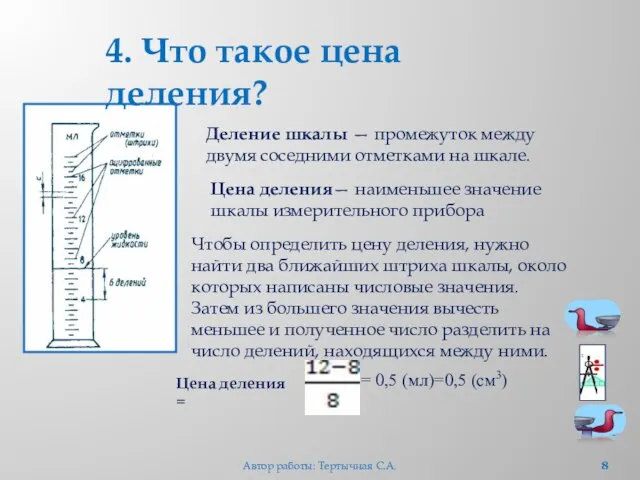
- 8. Деление шкалы — промежуток между двумя соседними отметками на шкале. Цена деления— наименьшее значение шкалы измерительного
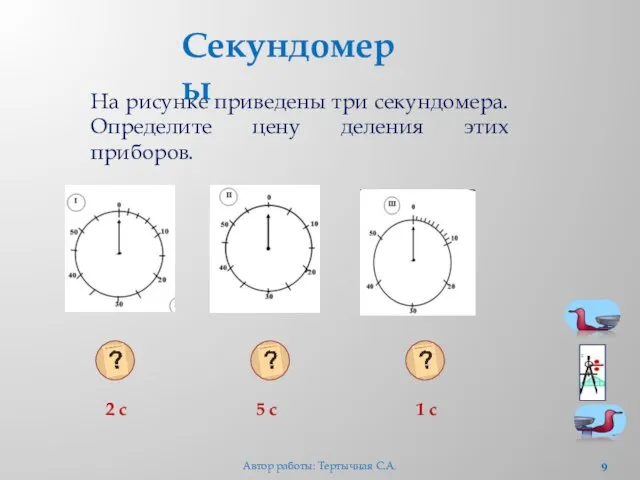
- 9. На рисунке приведены три секундомера. Определите цену деления этих приборов. Секундомеры 2 с 5 с 1
- 10. 1. Определите цену деления мензурки 5 мл 2,5 мл 5 мм 10 мл 2. Определите объём
- 11. 5. Единицы измерения физических величин Автор работы: Тертычная С.А. меню
- 12. 6. Единицы длины, площади, объёма, массы Автор работы: Тертычная С.А. меню
- 13. 7. Абсолютная погрешность измерения Точность измерений характеризуется погрешностью, или, как еще говорят, ошибкой измерений. Между терминами
- 14. Относительная погрешность измерения Для оценки границ погрешности при измерении величины договорились использовать среднюю абсолютную погрешность ∆x,
- 15. Вычисление погрешности Рассмотрим вычисление погрешностей на примере измерения длины болта 1) l1= 10,6 cм; 2) l2
- 16. Длина бруска Длину бруска измеряют с помощью линейки. Запишите результат измерения, учитывая, что погрешность измерения равна
- 17. t0 c I. Определите цену деления термометра II. Определите абсолютную погрешность термометра III. Какую температуру показывает
- 18. В мензурку налита вода. Запишите значение объёма воды, учитывая, что погрешность измерения равна половине цены деления
- 19. 8. Порядок физической величины В практике физических измерений возникают ситуации, когда приходится иметь дело с очень
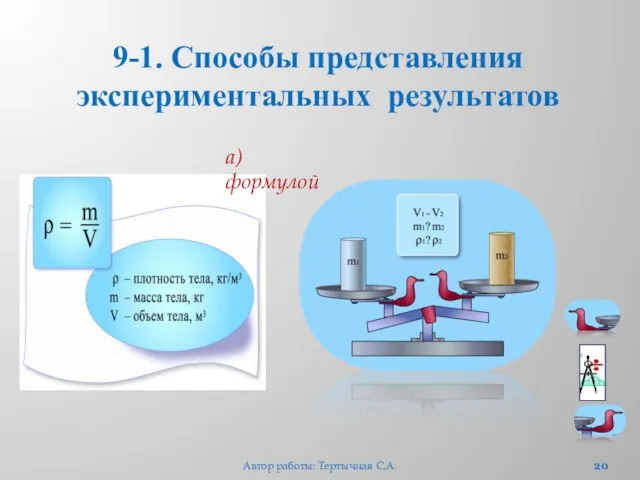
- 20. 9-1. Способы представления экспериментальных результатов а) формулой Автор работы: Тертычная С.А.
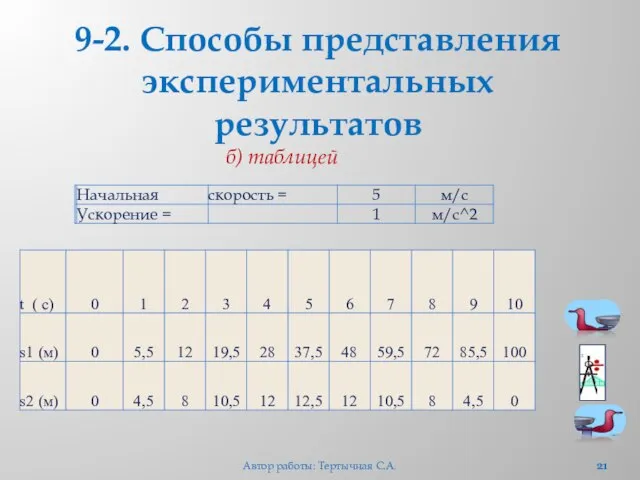
- 21. 9-2. Способы представления экспериментальных результатов б) таблицей Автор работы: Тертычная С.А.
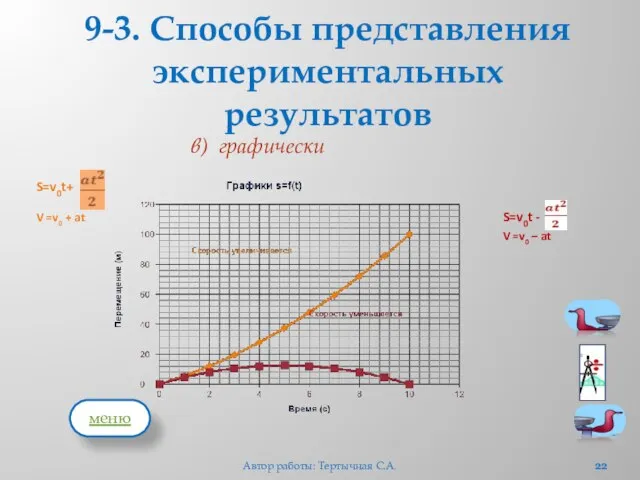
- 22. 9-3. Способы представления экспериментальных результатов в) графически Автор работы: Тертычная С.А. меню
- 23. Некоторые величины известны с очень большой точностью, число достоверных значащих цифр может быть равно шести и
- 25. Скачать презентацию
















 Ходовая часть автомобиля
Ходовая часть автомобиля Магнитное поле проводника с током
Магнитное поле проводника с током Дифракция света
Дифракция света Упругие свойства среды. Лекция 1.13
Упругие свойства среды. Лекция 1.13 Физика: явления, приборы, величины. Природа и техника
Физика: явления, приборы, величины. Природа и техника Расчет состава и толщины слоев гетероструктуры, обеспечивающей необходимое оптическое и электронное ограничение
Расчет состава и толщины слоев гетероструктуры, обеспечивающей необходимое оптическое и электронное ограничение Траектория - прямая линия
Траектория - прямая линия Законы регулирования
Законы регулирования Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Измерение линейных размеров штангенинструментом
Измерение линейных размеров штангенинструментом Световые кольца. Лазер
Световые кольца. Лазер Презентация на тему Волшебный мир магнетизма
Презентация на тему Волшебный мир магнетизма  Технические измерения
Технические измерения изические основы микроэлектроники
изические основы микроэлектроники Магнетизм. Структурно-логическая схема. Условные обозначения
Магнетизм. Структурно-логическая схема. Условные обозначения Дисперсия, интерференция, дифракция света
Дисперсия, интерференция, дифракция света Сборка, регулировка и испытание системы зажигания двигателей
Сборка, регулировка и испытание системы зажигания двигателей Уравнение неразрывности. Лекция 5
Уравнение неразрывности. Лекция 5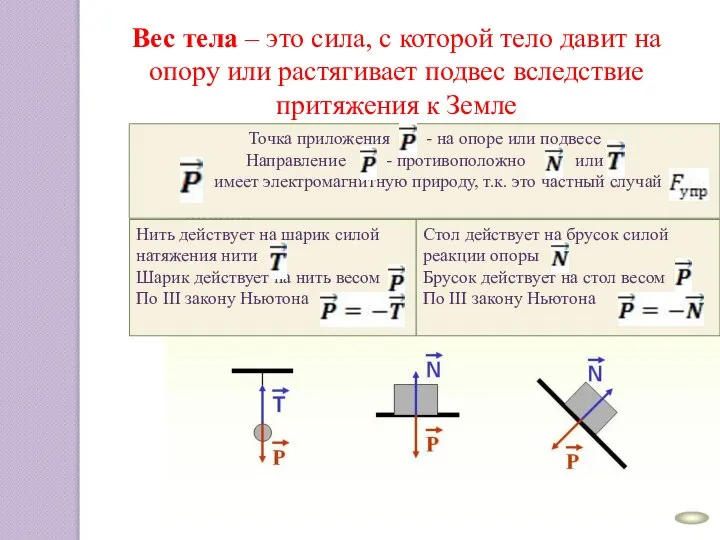 Вес тела
Вес тела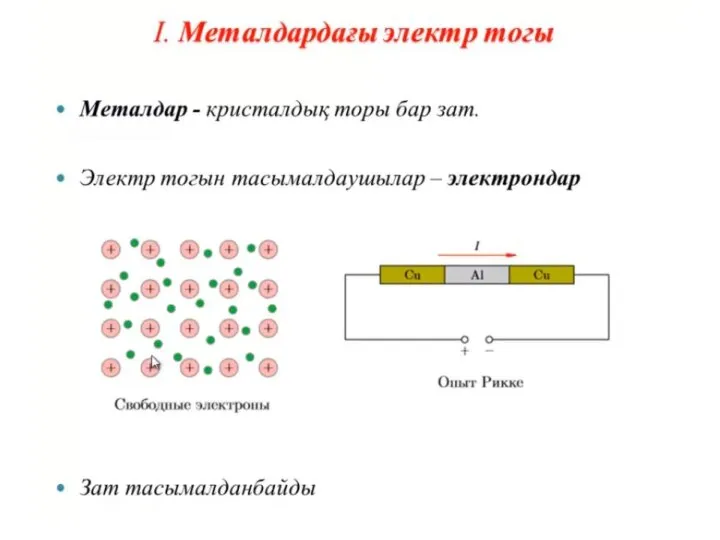 Әр түрлі ортадағы
Әр түрлі ортадағы План структурной оптимизации технологического процесса изготовления кузова модели SX11
План структурной оптимизации технологического процесса изготовления кузова модели SX11 Презентация на тему Примеры потребления электроэнергии
Презентация на тему Примеры потребления электроэнергии  Финишные методы обработки
Финишные методы обработки Кипение. Парообразование
Кипение. Парообразование Центр тяжести и устойчивое равновесие
Центр тяжести и устойчивое равновесие лекция 2 Динамика. Сила. Работа. Энергия. Импульс. (2)
лекция 2 Динамика. Сила. Работа. Энергия. Импульс. (2) Механическое движение
Механическое движение Освещение помещения. Оптимизация энергозатрат
Освещение помещения. Оптимизация энергозатрат