Слайд 2
1) Длина кривой.
Если подынтегральная функция f(x, y, z) ≡ 1, то из

определения КРИ-1 следует, что он равен длине кривой, по которой ведется интегрирование:
Слайд 3 2) Масса кривой.
Если подынтегральная функция γ (x, y, z) определяет плотность в

каждой точке кривой, то массу кривой можно найти по формуле
Слайд 43) Моменты кривой l:
статические моменты плоской кривой l относительно осей Ох

и Оу:
Слайд 5 момент инерции пространственной кривой относительно начала координат:
моменты инерции кривой относительно координатных осей:

Слайд 6 4) Координаты центра масс кривой вычисляются по формулам

Слайд 75) Работа силы , действующей на точку, движущуюся по кривой (АВ):

Слайд 8 Пример. Найти массу кривой с линейной плотностью
заданной в полярных координатах уравнением

ρ = 4φ, где
Слайд 10Пример. Вычислить работу векторного поля
вдоль отрезка прямой от точки А(-2;-3;1) до

точки В(1;4;2).
Слайд 11Решение. Найдем канонические и параметрические уравнения прямой АВ:

Слайд 13 Пример. Вычислить длину астроиды
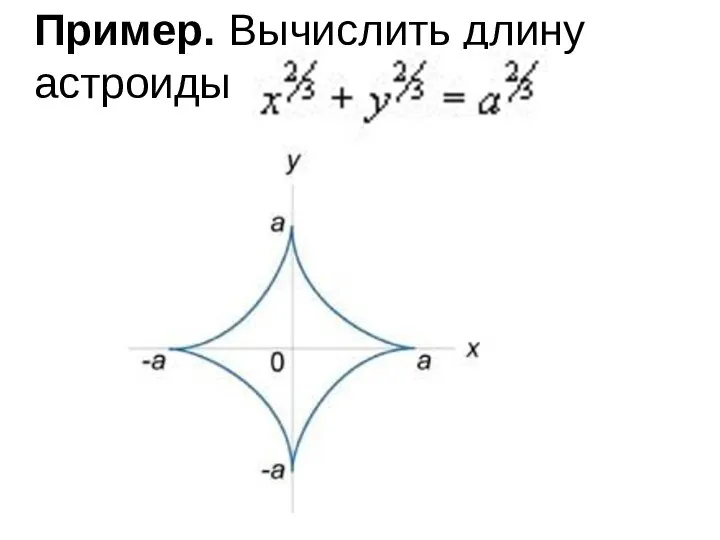
Слайд 14Решение. В силу симметрии, достаточно вычислить длину кривой, лежащей в первом квадранте,

и затем умножить результат на 4. Уравнение астроиды в первом квадранте имеет вид
Слайд 16Пример. Найти длину астроиды
x = a cos3t, y = a sin3t

Слайд 17Решение. Воспользуемся формулой
В нашем случае

Слайд 19 Поскольку кривая симметрична относительно осей координат, то

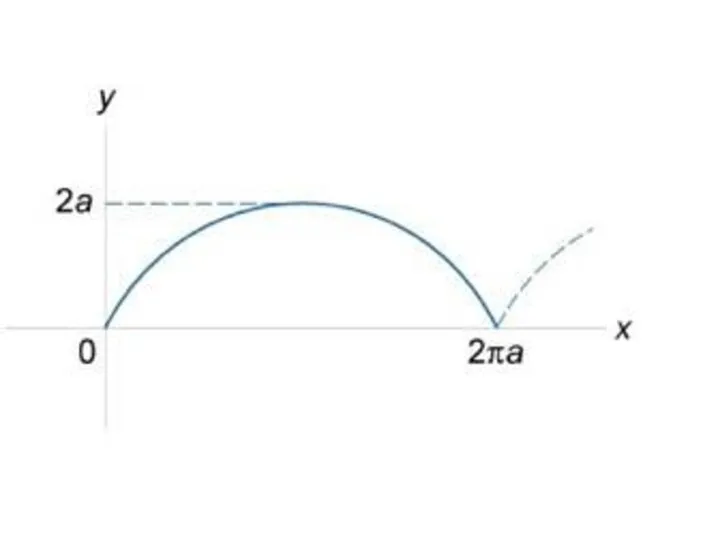
Слайд 20Пример. Найти длину циклоиды, заданной в параметрическом виде вектором
в интервале

Слайд 22 Решение. Воспользуемся формулой

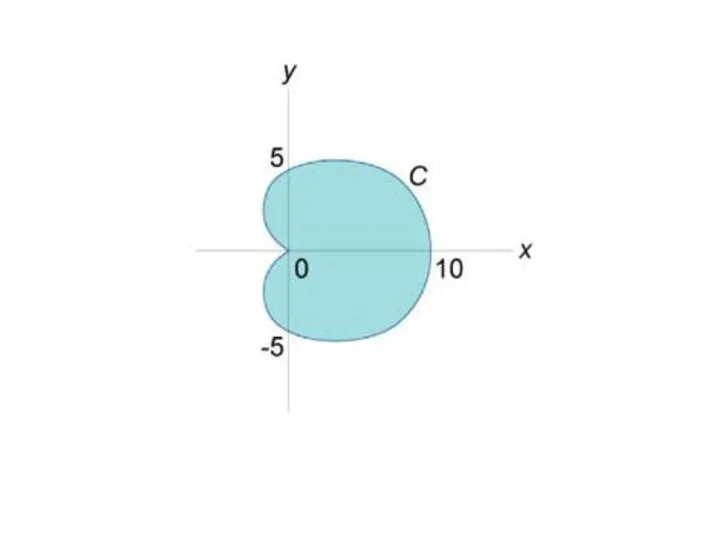
Слайд 25Пример. Найти длину кардиоиды, заданной в полярных координатах уравнением

Слайд 27Решение. Используем соотношение
В силу симметрии кардиоиды достаточно найти половину ее длины,

а затем удвоить полученный результат.
Слайд 28
Длина кардиоиды выражается в виде

Слайд 30
Так как при , то
Окончательно находим длину:

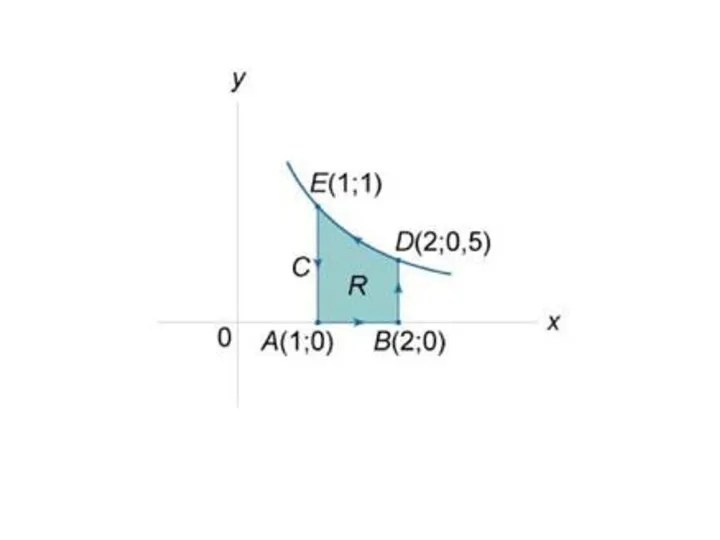
Слайд 33Пример. Найти площадь области, ограниченной гиперболой , осью Ox и вертикальными прямыми

x = 1, x = 2.
Слайд 35Решение. Вычислим площадь с помощью криволинейного интеграла.
Найдем отдельно каждый из интегралов.

Слайд 37Следовательно, площадь заданной области равна

Слайд 38Пример. Найти статические моменты дуги однородной астроиды
относительно осей координат.

Слайд 39Решение. Дуга астроиды однородна, следовательно, плотность в каждой точке постоянна. Пусть .

Запишем уравнение астроиды в параметрическом виде
где
Слайд 41По условию
следовательно,
dl = 3a sin t cos t dt

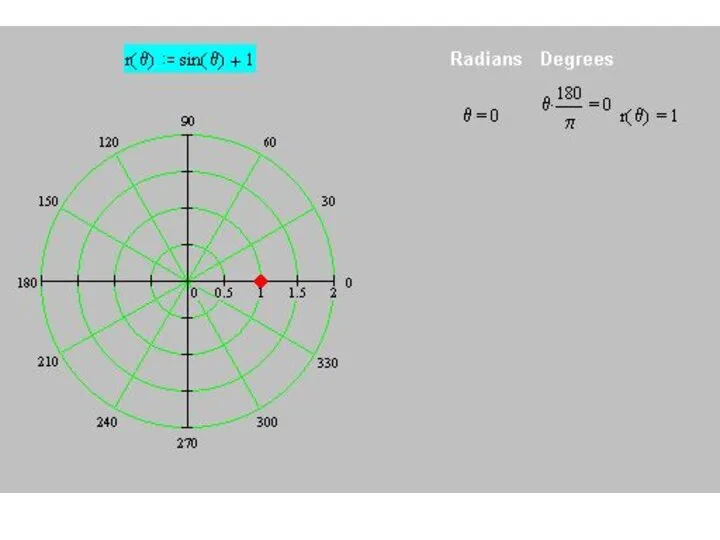
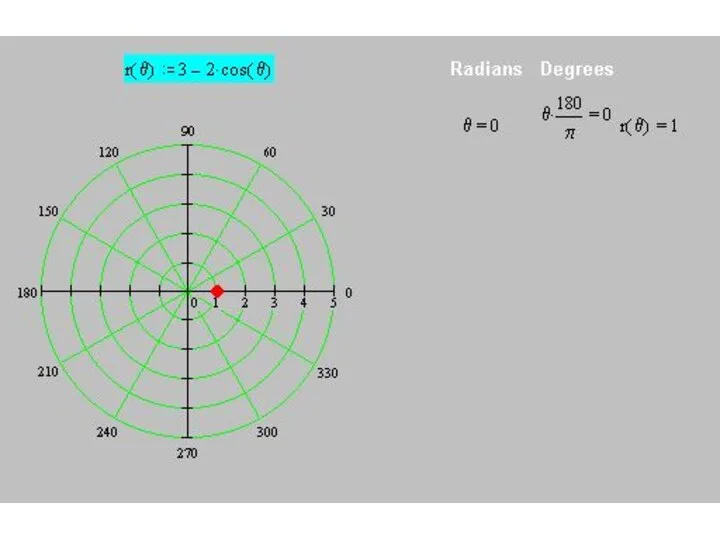
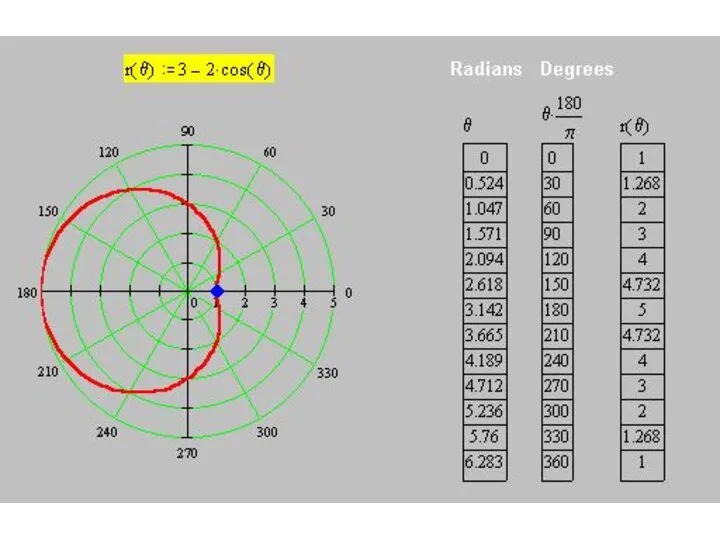
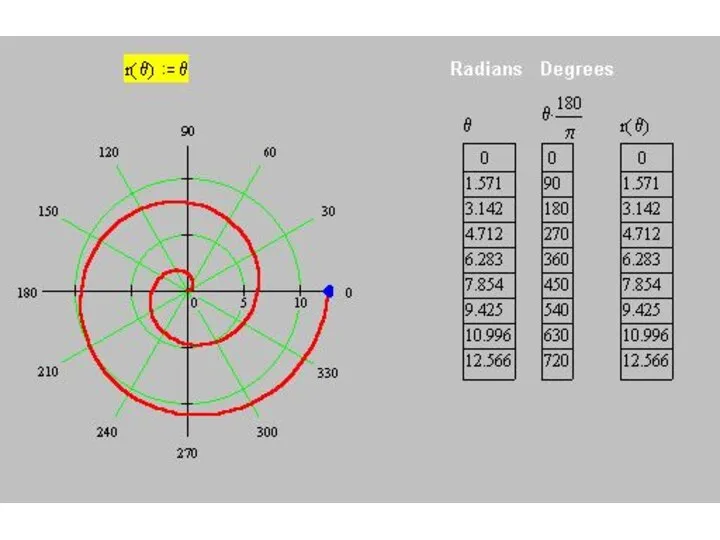
Слайд 47Построим кривую
r(θ) = 3 – 2 cos θ

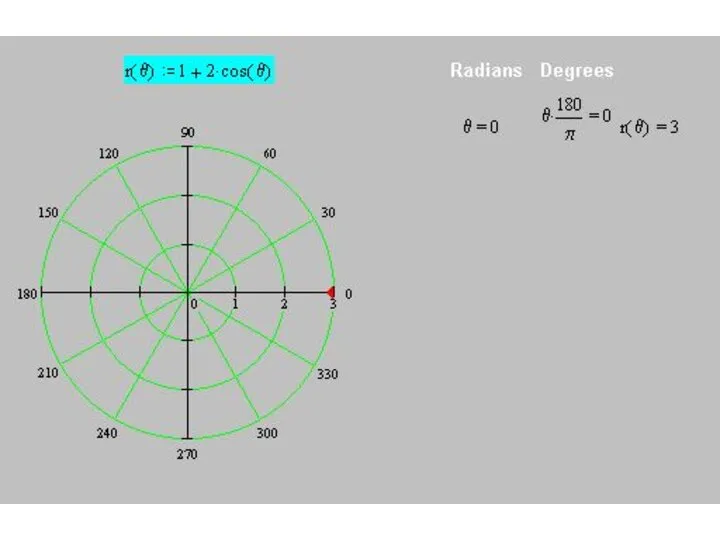
Слайд 50Построим кривую
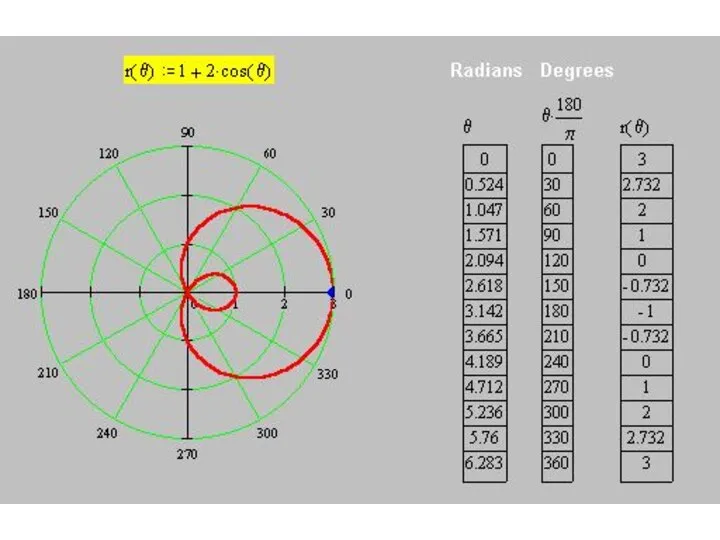
r(θ) = 1+ 2 cos θ

Слайд 53Построим кривую
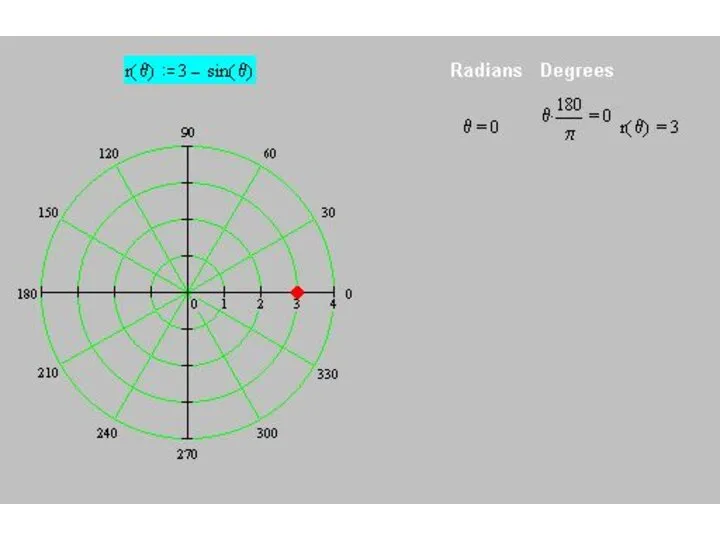
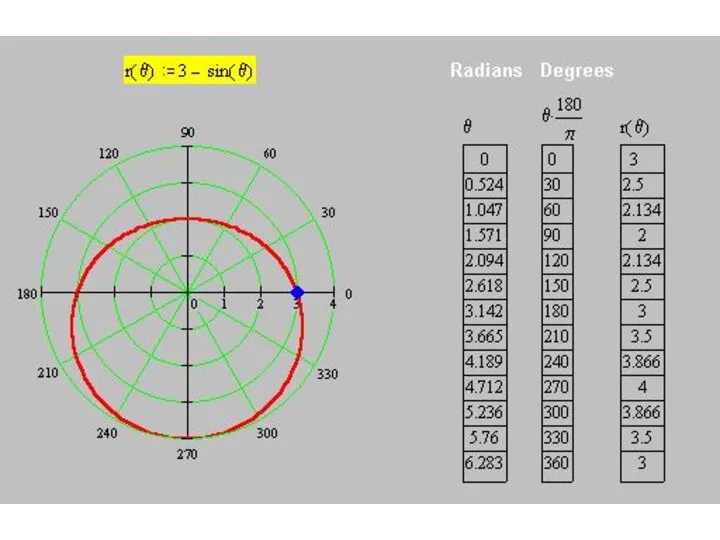
r(θ) = 3 – sin θ

Слайд 56Построим кривую
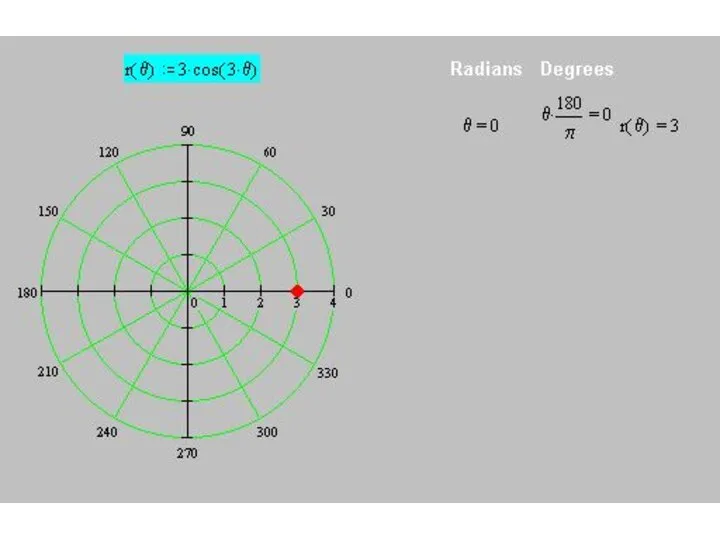
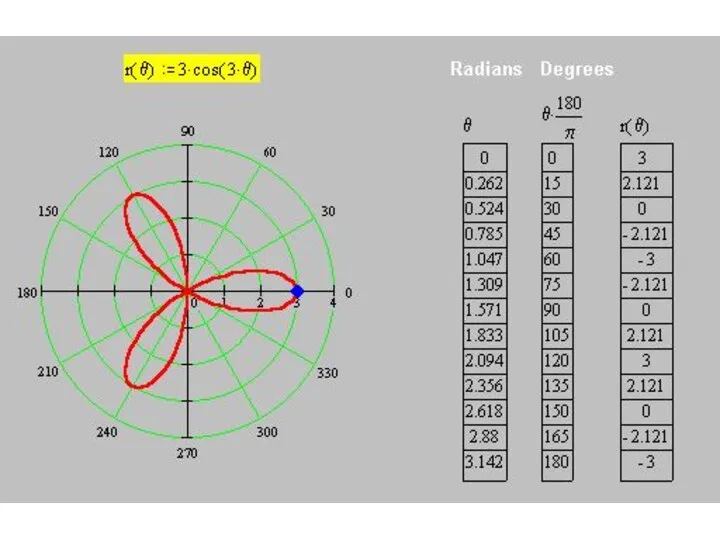
r(θ) = 3 cos (3θ)

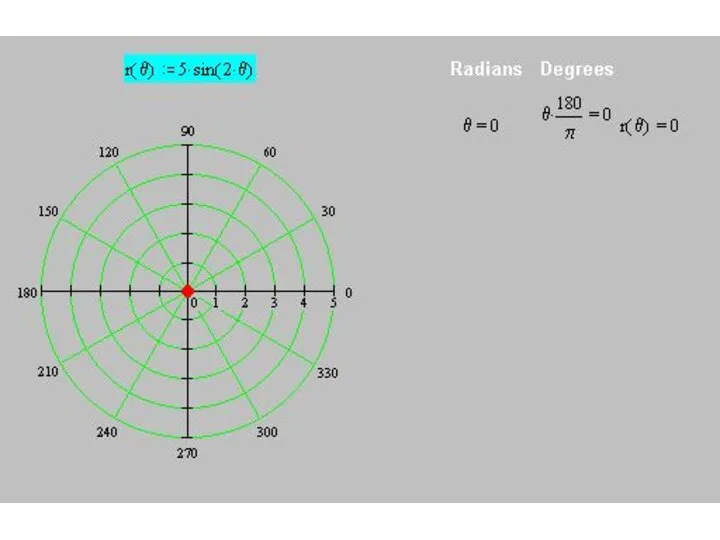
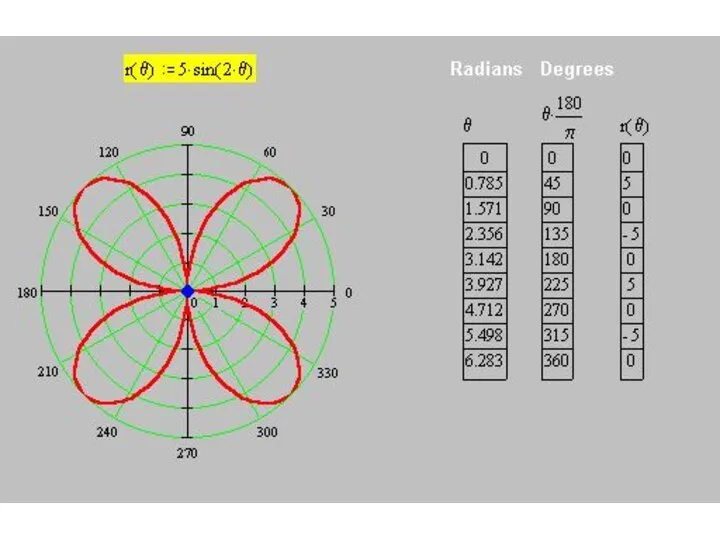
Слайд 59Построим кривую
r(θ) = 5 sin (2θ)











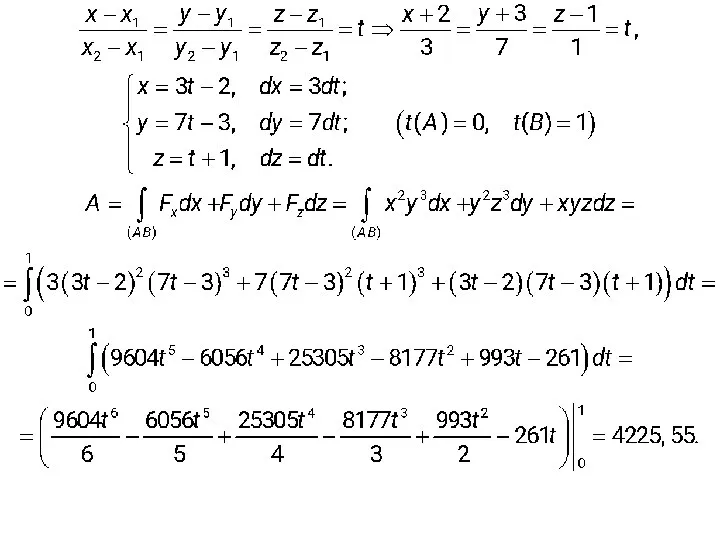


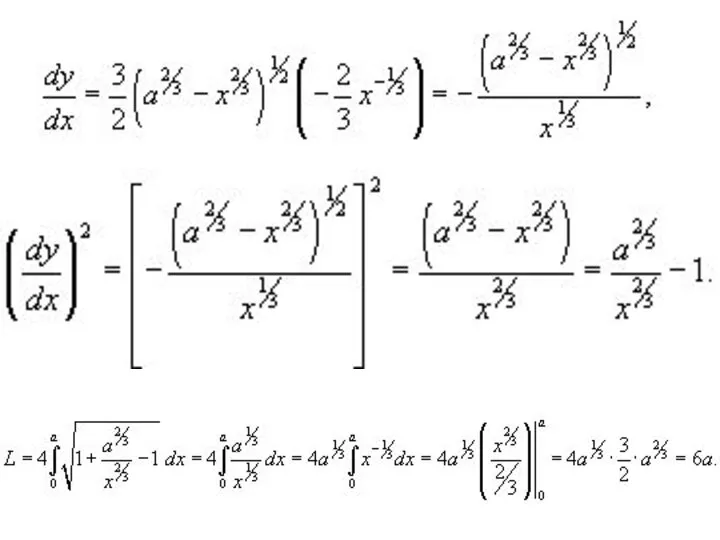


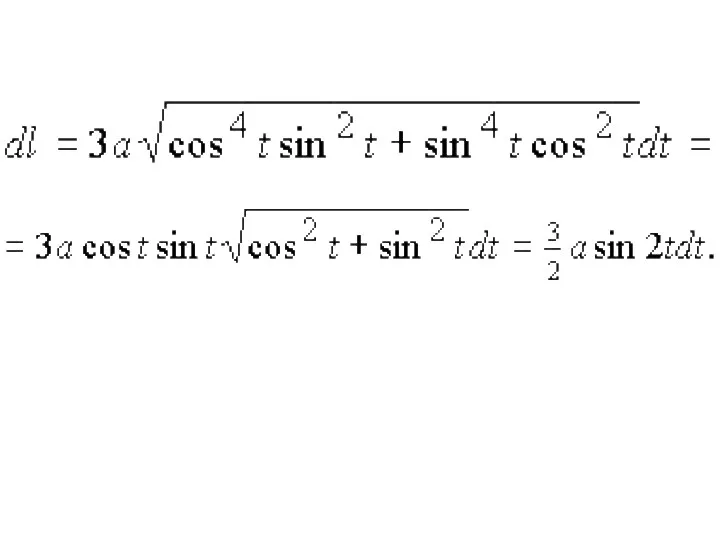








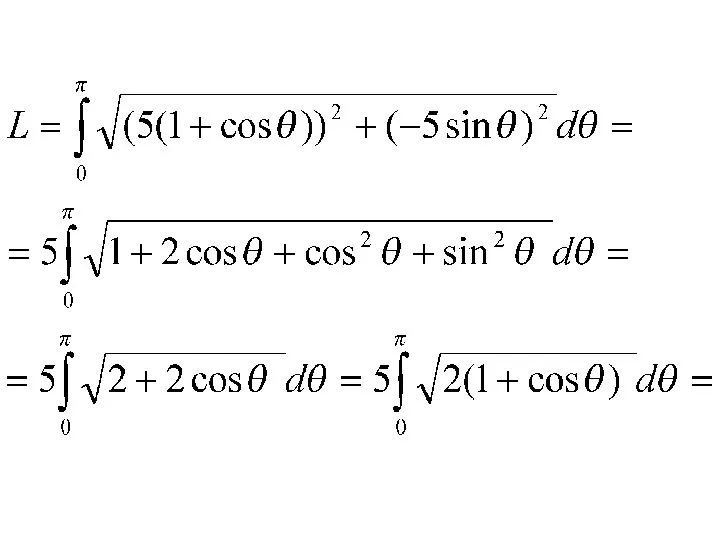

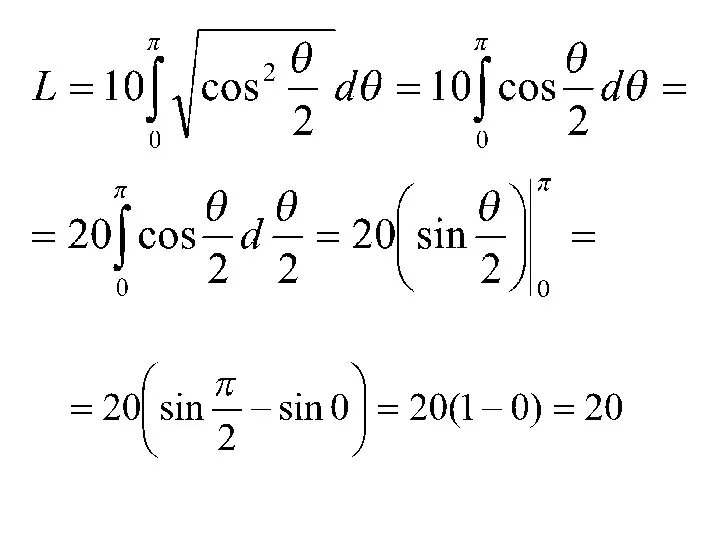



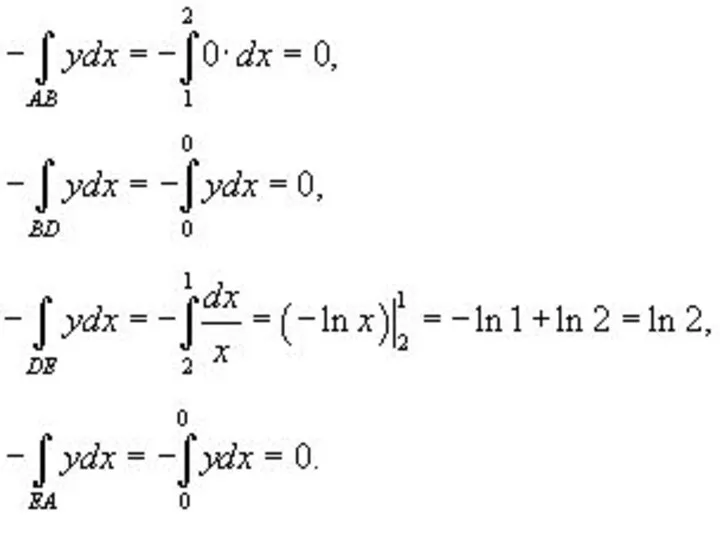



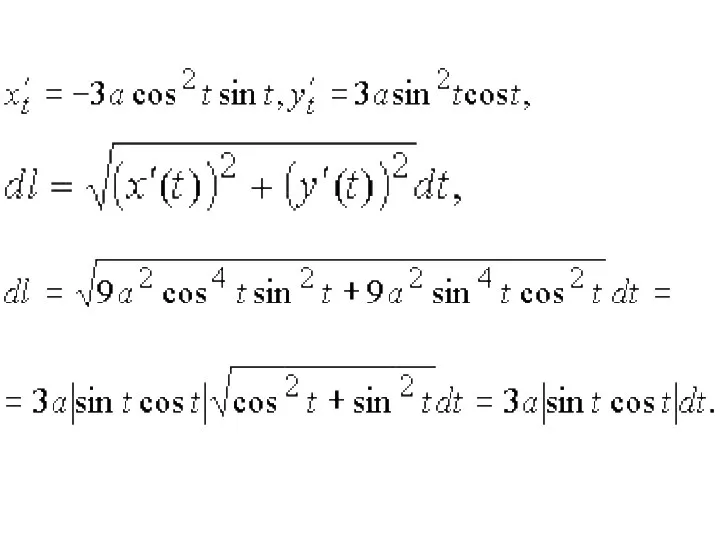

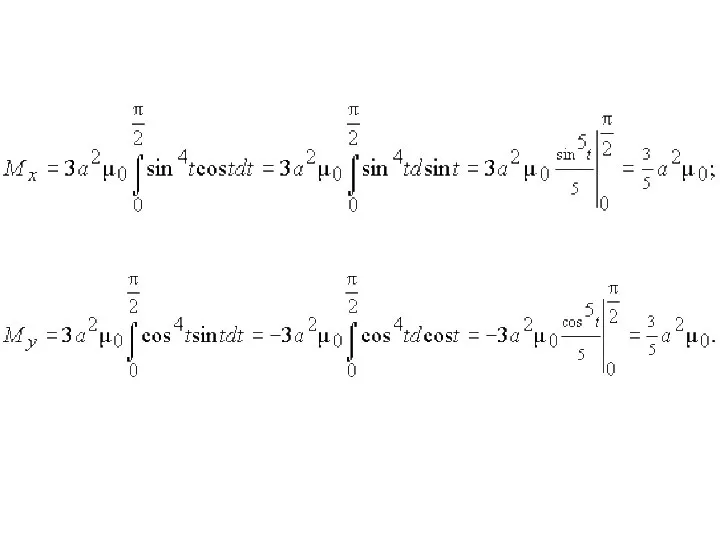










 Электрические явления
Электрические явления Квантовые вычисления
Квантовые вычисления Презентация на тему Движение тела, брошенного вертикально вверх
Презентация на тему Движение тела, брошенного вертикально вверх  Взаимодействие проводников с током
Взаимодействие проводников с током Редукторы. Типы передачи
Редукторы. Типы передачи Законы постоянного тока
Законы постоянного тока Динамика. Законы Ньютона
Динамика. Законы Ньютона Единицы измерения скорости. Формула скорости
Единицы измерения скорости. Формула скорости Формульный диктант Кинематика, законы Ньютона, сохранения, статика
Формульный диктант Кинематика, законы Ньютона, сохранения, статика Наноматериалы и нанотехнологии. Методы синтеза Введение
Наноматериалы и нанотехнологии. Методы синтеза Введение Оптические иллюзии в жизни
Оптические иллюзии в жизни Фотоэффект. Самостоятельная работа
Фотоэффект. Самостоятельная работа Силы трения
Силы трения Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Диэлектрики. Введение
Диэлектрики. Введение Общая физика
Общая физика Космические скорости. 10 класс
Космические скорости. 10 класс Теория Бора для атома водорода
Теория Бора для атома водорода Lek_PP_Operatorny_metod
Lek_PP_Operatorny_metod Физика, как наука и основа естествознания
Физика, как наука и основа естествознания Олимпийские игры в Афинах 2004 год
Олимпийские игры в Афинах 2004 год Презентация на тему Радиация: проблемы и перспективы
Презентация на тему Радиация: проблемы и перспективы  Решение качественных и расчетных задач по физике
Решение качественных и расчетных задач по физике Презентация на тему Вычисление массы и объёма тела по его плотности
Презентация на тему Вычисление массы и объёма тела по его плотности  Сила тяжести
Сила тяжести Датчики термоанемометров
Датчики термоанемометров История развития. Механика
История развития. Механика Порівняння швидкостей різних рухомих тіл
Порівняння швидкостей різних рухомих тіл