Слайд 2СОДЕРЖАНИЕ
Равнодействующая пространственной системы сходящихся сил.
Аналитическое условие равновесия.
Геометрическое условие равновесия.

Слайд 3Равнодействующая пространственной системы сходящихся сил
Пространственная система сходящихся сил – это
система
сил, линии действия которых не лежат в одной
плоскости, но пересекаются в одной точке.
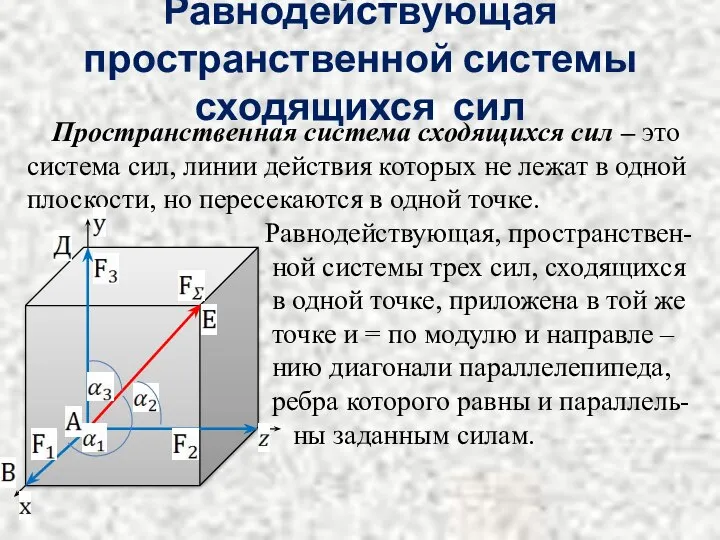
Равнодействующая, пространствен-
ной системы трех сил, сходящихся
в одной точке, приложена в той же
точке и = по модулю и направле –
нию диагонали параллелепипеда,
ребра которого равны и параллель-
ны заданным силам.
Слайд 4 Если действующие на тело три силы образуют м/у
собой прямые углы,

то при их сложении образуется
прямоугольный параллелепипед, диагональ которого:
Направление определяется углами:
Слайд 5Аналитическое условие равновесия.
Проекция равнодействующей системы сил на ось
равна алгебраической сумме

составляющих сил на ту
же ось:
Модуль равнодействующей:
Слайд 6 Для равновесия пространственной системы сходя-
щихся сил необходимо и достаточно, чтобы алгеб-
раическая

сумма проекций всех сил на каждую из
трех осей координат были равны нулю:
Слайд 7Геометрическое условие равновесия.
Равнодействующая любого числа сходящих сил.
расположенных в пространстве, равна

замыкающей
стороне многоугольника, стороны которого равны и
параллельны заданным силам (правило силового
многоугольника ).
Пространственная система сходящих сил уравно-
вешена, если многоугольник сил замкнут, т.е. FΣ = 0.
Слайд 8Момент силы относительно оси.
модули
проекций сил на плоскости,
перпендикулярные той оси,
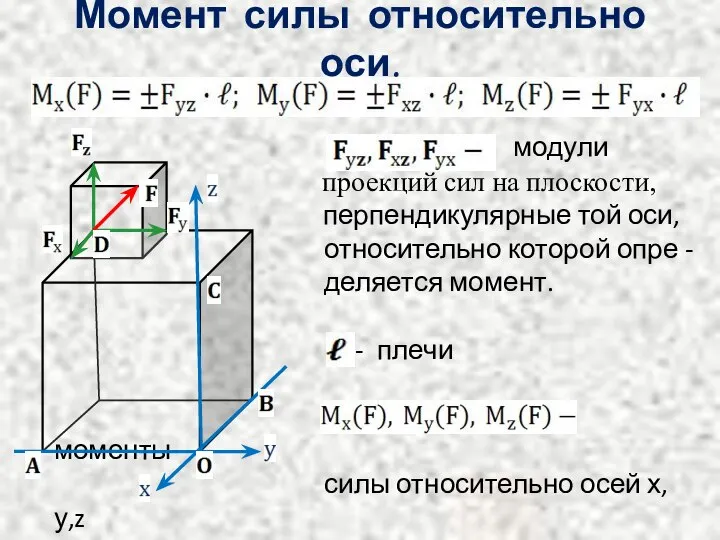
относительно которой опре -
деляется момент.
- плечи
моменты
силы относительно осей х,у,z
Слайд 9
Момент силы относи-
тельно оси называется
алгебраическая(скаляр-
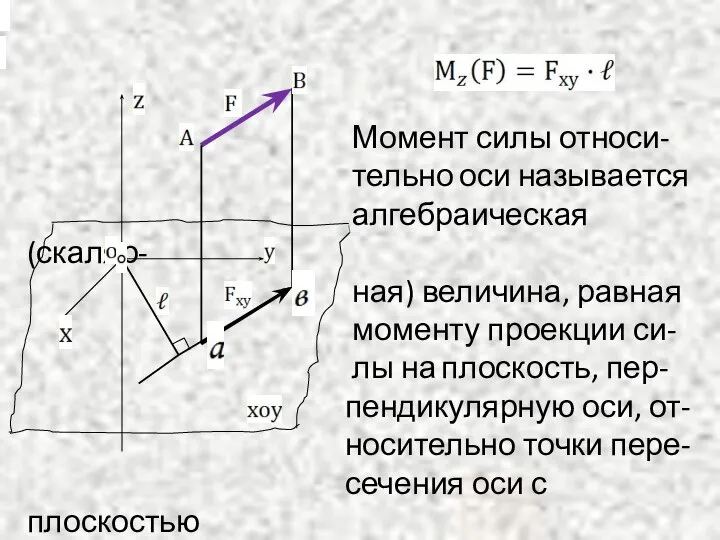
ная) величина, равная
моменту проекции си-
лы на плоскость, пер-
пендикулярную оси, от-
носительно точки пере-
сечения оси с плоскостью
Слайд 10Частный случай:
Момент силы относительно оси равен нулю, если
сила и ось
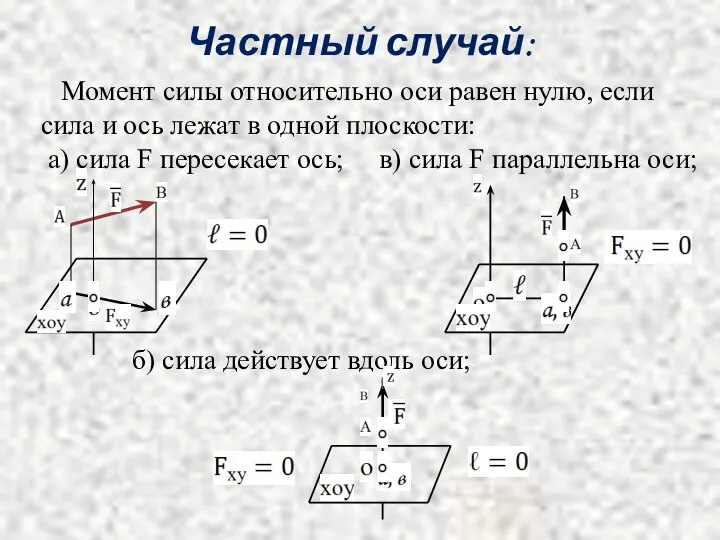
лежат в одной плоскости:
а) сила F пересекает ось; в) сила F параллельна оси;
б) сила действует вдоль оси;
Слайд 11Произвольная пространственная система сил.
Спроецируем главный вектор на оси:
Разложим главный момент
на
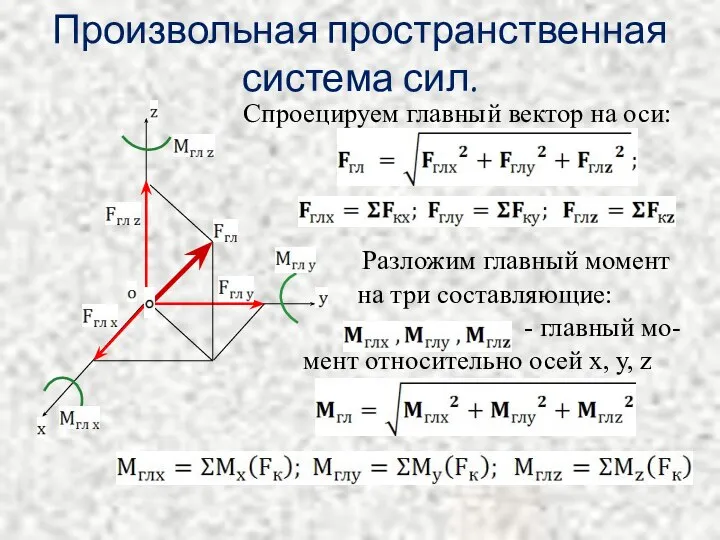
три составляющие:
- главный мо-
мент относительно осей х, у, z
Слайд 12 Когда пространственная система сил приводится к силе и к паре, возможны

четыре результата:
1. - система сил приводится к равнодействующей , равной ;
2. - система сил равнодействующей не имеет;
3. - система сил эквивалентна паре сил;
4. - система сил уравновешена.
Слайд 13Условия равновесия произвольной пространственной системы сил.
Система находится в равновесии, если

относительно произвольно выбран-
ной точки приведения. Следовательно:












 Звуки природы и звуки космоса. Что их объединяет
Звуки природы и звуки космоса. Что их объединяет Презентация на тему Экономия использования энергетических ресурсов на земле
Презентация на тему Экономия использования энергетических ресурсов на земле  Физика в игрушках
Физика в игрушках Направление индукционного тока
Направление индукционного тока Элементы трехфазных цепей
Элементы трехфазных цепей 33_1_PrZ_t_3_1_3_ElStatika_10SENT2022
33_1_PrZ_t_3_1_3_ElStatika_10SENT2022 Сухой электростатический перенос
Сухой электростатический перенос Уход за швейной машиной
Уход за швейной машиной Задачи на соединение проводников
Задачи на соединение проводников Электричество и магнетизм
Электричество и магнетизм Собственный механический и магнитный моменты электрона. Спин
Собственный механический и магнитный моменты электрона. Спин Агрегатные состояния вещества
Агрегатные состояния вещества Импульс тела. Задачи
Импульс тела. Задачи Электромагнитные волны. Явления интерференции и дифракции
Электромагнитные волны. Явления интерференции и дифракции Методы и приёмы решения задач по физике
Методы и приёмы решения задач по физике Задачи на движение
Задачи на движение Однородные уравнения. Уравнения, приводящиеся к однородным
Однородные уравнения. Уравнения, приводящиеся к однородным Решение качественных и расчетных задач по физике
Решение качественных и расчетных задач по физике История радио
История радио Сила трения
Сила трения Классификация зубчатых передач
Классификация зубчатых передач Испарение и конденсация. Поглощение и выделение энергии
Испарение и конденсация. Поглощение и выделение энергии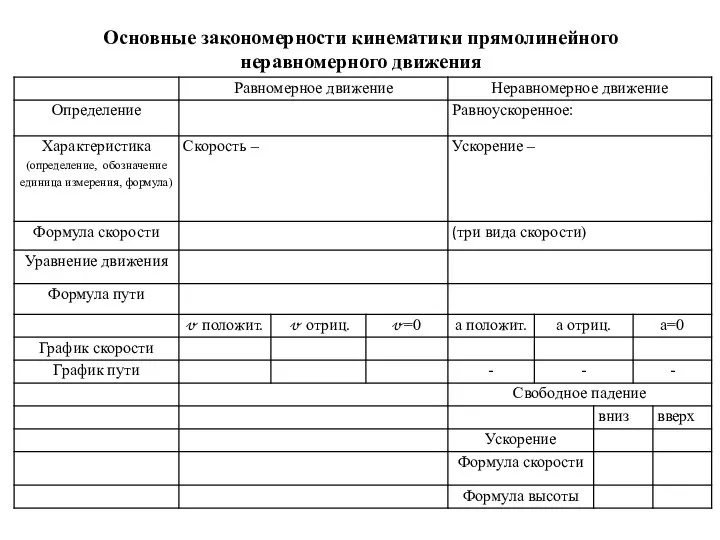 Закономерности кинематики прямолинейного неравномерного движения. Таблица
Закономерности кинематики прямолинейного неравномерного движения. Таблица Тангенс угла диэлектрических потерь, измерение показателя диэлектрических потерь
Тангенс угла диэлектрических потерь, измерение показателя диэлектрических потерь Презентация на тему Механическое движение
Презентация на тему Механическое движение  Механические волны
Механические волны Что изучает физика. Наблюдения и опыты
Что изучает физика. Наблюдения и опыты Атомные спектры
Атомные спектры