Расчет направляющих. Анализ напряжений и деформаций направляющих в процессе работы ловителя

В расчетах направляющих следует принять во внимание три эксплуатационных условия:
1) условия движения с нагрузкой, неравномерно распределенной на полу кабины;
2) работа ловителя;
3) загрузка и разгрузка, соответственно.
В большинстве национальных стандартов, расчет напряжения в направляющих проводится для условия 2), а расчет упругой деформации касается совершенно разных условий работы, а именно 1) и / или 3).

7.2.1. Анализ напряжений и деформаций направляющих в процессе работы ловителя
Направляющая будет рассматриваться как неразрезная балка с изменяющимся количеством опор. Как методы решения могут использоваться Теорема Трех Моментов и Метод Конечных Элементов.
Направляющая подвержена комбинированному воздействию тормозной силы Fb, действующей параллельно продольной оси направляющей, и внешнего момента Fb∙e (рис. 7.10).
Внешний момент возникает из-за эксцентричного расположения тормозной силы Fb которое представлено расстоянием е (см. рис. 7.3).

Расположение тормозной силы Fb

Изгибающий момент Moz зависит от количества пролетов балки и внешнего момента Fb ∙ е (от величины и расположения).
Уравнения для максимального изгибающего момента Moz как функции z, значения и расположение экстремумов локальных функций даны в табл.7.4 для
Fb ∙ е, действующего в I пролете балки, и в табл.7.5 для Fb∙e в пролете II. Максимальный изгибающий момент всегда находится в точке приложения внешнего момента Fb ∙ е.

Рис.7.11. Изменение максимального изгибающего момента MQZ вдоль неразрезной трехпролетной балки

Расчет напряжений в направляющих
Важнейшее значение имеет расположение ловителя.
Когда ловитель расположен под полом кабины, захват направляющих может происходить в пролете I.
Если ловитель смонтирован над потолком кабины, направляющие могут быть захвачены только во II пролете Расчет будет проводиться с учетом комбинированного действия поперечного и продольного изгиба.

(А) Пролет I
Изгибающий момент в любой точке левее Fb х е определяется следующей
окончательной формулой:
где М1 - момент опоры 1, (Н м), z - изменяющееся расстояние от левой опоры (0) до точки, в которой рассчитывается изгибающий момент, (мм), ξ -расстояние от левой опоры (0) до точки, в которой действует внешний момент Fb ∙ е, (мм).
где Е - модуль упругости (Юнга), (Н/мм2), Jx - момент инерции площади
поперечного сечения направляющей относительно оси х-х.

Что касается оценки величины а, могут иметь место три теоретических случая.
(a) α ∙ l< π /2
Это единственный случай, который может иметь место на практике.
Экстремум функции лежит вне пролета I. Это значит, что максимальная величина изгибающего момента остается в точке приложения Fb∙e и влияние воздействия тормозной силы Fb на продольную устойчивость не имеет решающего значения из-за жесткости направляющей в плоскости, перпендикулярной оси х-
х поперечного сечения направляющей.
(b) а ∙l = π/2
Экстремум функции имеет место на правой опоре пролета I (опора 1).
(c) а ∙l > π/2

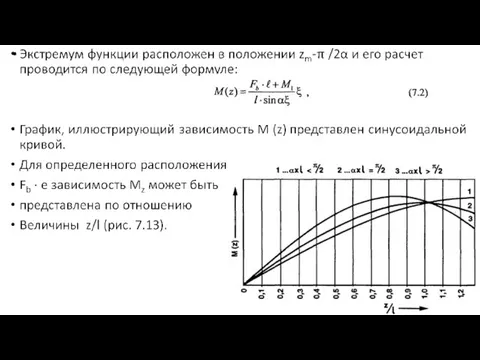
Экстремум функции расположен в пролете I. Для ξ > zm это значит, что изгибающий момент, действующий левее Fb ∙ е больше, чем в точке приложения Fb ∙ е и имеет решающее значение для расчета прочности направляющей.
Все три случая проиллюстрированы на рис. 7.13.
В случае (а) синусоидальные кривые могут быть построены для определенных положений внешнего момента Fb ∙ е, определяемого расстоянием ξ от левой опоры пролета I (опора 0).
Кривые на рис. 7.14 были построены для параметров пассажирского лифта небольшой грузоподъемности (номинальная грузоподъемность 320 кг, номинальная скорость 0,7 м/с).

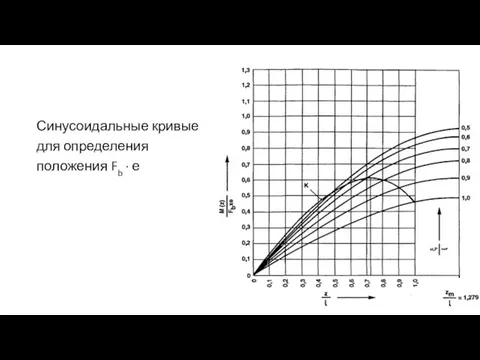
Синусоидальные кривые
для определения
положения Fb ∙ е

Кривые на рис. 7.14 были построены для параметров пассажирского лифта небольшой грузоподъемности (номинальная грузоподъемность 320 кг, номинальная скорость 0,7 м/с).
Так как. максимальный изгибающий момент всегда действует в точке приложения Fb ∙ е, возможно начертить график зависимости максимального изгибающего момента от величины отношения
z / l, т.е для точки приложения момента Fb ∙ е (кривая К).
Для
мы получаем критическое значение ξm положения точки действия Fb ∙ е.

Когда Fb ∙ е находится в этой точке, изгибающего момента Mmax достигает абсолютного максимума. Обе величины ξm и Mmax уже были даны в табл. 7.4 (т.е. ξm = zm = 0,7251 1 и Мmax = Mozm = 0,6129 Fb ∙ е для неразрезной пяти пролетной балки).

(В) Пролет II
Формулы, полученные из того же самого первоначального уравнения с помощью тех же самых математических методов, более сложные, чем для пролета I.
Изгибающий момент:
Где
С1 = М1
и
М2 - момент на правой опоре пролета II (опора 2).

Расположение экстремума функции.
Постоянные интегрирования C1 и С2 зависят от моментов на опорах, т.е.
также от расположения момента Fb ∙ е.
Поэтому, в отличие от пролета I, расположение максимального изгибаю-
щего момента (zm) в данном случае является функцией расположения
Fb ∙ е.( ξm).
Максимальная величина изгибающего момента:

Кривая зависимости M(z), может быть получена путем наложения двух
отдельных кривых: С2 ∙ sin αz и C1 ∙ cos αz с различными амплитудами. Амплитуды отличаются в зависимости от расположения Fb ∙ е. Полученная кривая характеризуется разной амплитудой и фазовым сдвигом.
Заменив исходные данные техническими параметрами реального лифта, будет легко показать, что С2 всегда больше нуля, а С1 может быть больше, меньше или равно нулю в зависимости от расположения ξ момента Fb ∙ е. Существует предельное значение которое, например, для балки пяти или более пролетов имеет величину 0,3804 1, измеренную от левой опоры (1).

Кроме того,
C1 < 0 для ξ > 0,3804 1 и фазовый сдвиг z0>0;
M(z) смещается в правом направлении.
С1 = 0 для ξ = 0,3804 1 и z0 = 0.
С1 > 0 для ξ < 0,3804 1 и z0 < 0;
М (z) смещается влево.
Фазовый сдвиг:

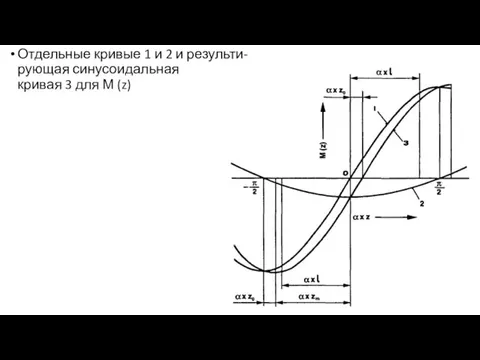
Отдельные кривые 1 и 2 и результи-
рующая синусоидальная
кривая 3 для М (z)

Расчет прогиба
Следует рассмотреть два случая
(A) Fb ∙ е действует у правой опоры (1) пролета I. Этот случай имеет решающее значение, когда ловитель расположен под полом кабины.
Положение максимального прогиба:
Максимальный прогиб:

(В) Fb ∙ е действует у правой опоры (2) пролета II. Этот случай имеет ре-
шающее значение, когда ловитель установлен над крышей кабины.
Мы получаем квадратное уравнение для zm, корни которого:
где
Максимальный прогиб

7.2.2. Силы, действующие на направляющие в процессе нормальной работы. Классы загрузки
При нормальных условиях эксплуатации нагрузка может быть распределена неравномерно в двух перпендикулярных направлениях.
Силы, действующие на направляющие из-за неравномерного распределения нагрузкиy

На рис. показана схема направляющих и действующих на них сил,
обусловленных неравномерной загрузкой кабины. Силы Fy действуют в плоскости направляющих (у-у), тогда как Fx1 и Fx2 действуют в плоскостях х-х перпендикулярных плоскости у-у.
Каждая направляющая подвергается изгибу под действием силы Fy, а также изгибу и кручению силой Fx.

Силы могут быть рассчитаны по следующим формулам:
где Q - номинальная грузоподъемность (кг), gn - стандартное ускорение свободного падения (м/с2), еу и ех - эксцентрицитеты нагрузки в кабине (мм), b - ширина кабины (мм), с - глубина кабины (мм), h - вертикальное расстояние между центровыми линиями направляющих башмаков кабины (мм).

Подставив определенные значения эксцентрицитетов ех и еу в уравнения 7.11, 7.12 и 7.13, мы получим величину поперечных сил, действующих на направляющие в нормальном эксплуатационном режиме.
Например, для ех = с/8 и еу = b/8:

Силы, действующие на направляющие противовеса
Поперечные силы, действующие на направляющие противовеса, могут
быть вызваны смещением центра тяжести относительно точки подвески.
Для расчетных целей предполагается, что масса противовеса смещена относительно центра на 20 мм в плоскости направляющих (у-у) или в перпендикулярной плоскости (х-х).
Основные положения расчета силы, действующей на направляющие в
нормальных условиях работы, для грузовых лифтов определены в большинстве стандартов. Положения, касающиеся определения классов загрузки, включенные в Британский стандарт BS 5655:Part 9, наиболее поучительны и поэтому будут здесь представлены.

Классы загрузки (в соответствии с BS 5655: Part 9)
Класс А: Загрузка пассажирами и обычными грузами.
Класс А загрузки применяется, когда загрузка и разгрузка кабины производится вручную или с использованием ручных тележек и когда масса любого единичного груза или любой ручной тележки с грузом не превышает четверти номинальной грузоподъемности.
При определении горизонтальных сил, действующих на направляющие, предполагается, что 50% номинальной нагрузки расположено на расстоянии от точки подвески:
(a) равном одной четвертой ширины кабины, т.е. еу = Ы4 или
(b) равном одной четвертой глубины кабины, т.е. ех = с/4.

Класс В: Загрузка транспортных средств с двигателем.
Загрузка класса В применяется, когда лифт используется исключительно
для перевозки тележек с двигателем или пассажирских автомашин, соответствующих номинальной грузоподъемности лифта.
При определении горизонтальных сил, действующих на направляющие,
предполагается, что полная номинальная нагрузка расположена на расстоянии от точки подвески:
(a) равном одной восьмой ширины кабины, т.е. еу = b/8 или равной одной второй ширины кабины минус 1220 мм, т.е. (0,5b-1220), что бы ни было больше.
(b) равном одной двенадцатой глубины кабины, т.е. е, = с/12.

Класс С: Загрузка тяжелых грузов
Загрузка класса С применяется гам, где тележки с двигателем или ручные
тележки используются для перевозки вместе с грузом, превышающим загрузку
класса А, или где транспортируются сосредоточенные грузы.
При определении горизонтальных сил, действующих на направляющие,
предполагается, что полная номинальная нагрузка расположена на расстоянии
от точки подвески:
(a) равном одной четвертой ширины кабины, т.е. еу = b/4 или
(b) равном одной четвертой глубины кабины, т.е. ех = с/4.
В стандарте BS 5655:Part 9 оговариваются условия загрузки кабины, когда она находится в стационарном положении, на уровне этажа.
Для классов В и С предполагается, что одна вторая номинальной нагрузки приложена к порогу кабины, что приводит к появлению горизонтальных сил,
действующих на направляющие в направлении х-х. Если известна фактическая
нагрузка порога кабины, её следует учитывать вместо величины Q/2 ∙ gn.

7.2.3. Международные стандарты расчета направляющих
Британский Стандарт BS 5655:Part 9
Напряжение в направляющей в в процессе работы ловителя σ определяется уравнением:
где Fb, - тормозная сила, действующая на одну направляющую, (Н),
S - площадь поперечного сечения направляющей, (мм2), е - эксцентриситет
тормозной силы (горизонтальное расстояние от оси х-х поперечного сечения направляющей до точки воздействия башмаков ловителя, (мм),
Wx - момент сопротивления изгибу относительно оси х-х, (мм3), lk-максимальное расстояние между кронштейнами направляющих, (мм), Е - модуль упругости (Юнга) материала направляющей, (Н/мм2) и Jx - момент инерции площади поперечного сечения направляющей относительно оси х-х, (мм4).

Прогиб направляющей в процессе работы ловителя ограничен до максимума 0,25 длины механически обработанной поверхности направляющего рельса для того, чтобы избежать риска выхода направляющих башмаков с направляющей.
С учетом этого условия, максимальная величина тормозной силы ловителя определяется по формуле:

Тормозная сила Fb определена в BS 5655: Part 9 и также в Европейском Стандарте EN 81-1.
В общем, тормозная сила в случае применения двух направляющих рассчитывается по формуле
где К - масса кабины (кг) и а - максимально допустимое ускорение тор-
можения кабины, (м/с2).

Практические значения тормозной силы (допуская, что gn = 10 м/с2) следующие:
для ловителя резкого торможения, исключая тип с заклинивающим роликом,
для ловителя с заклинивающим роликом,
для ловителя плавного торможения,

Напряжение в направляющих, рассчитанное по уравнению 7.14, не должно превышать следующие значения:
140 Н/мм2 для предела прочности стали 370 Н/мм2
170 Н/мм2 для предела прочности стали 430 Н/мм2
210 Н/мм2 для предела прочности стали 520 Н/мм2.
Величина модуль упругости (Юнга) Е = 2,07 х 105 Н/мм2.
Критерии качества, основанные на учете напряжений и деформации, при работе в нормальном эксплуатационном режиме следующие: направляющая рассматривается как простая балка с определенной степенью фиксации в опорных точках и, предполагается, что поперечная сила действует в середине расстояния между креплениями направляющей.

Тогда максимальные напряжения изгиба рассчитываются по формулам 7.17 и 7.18:
Постоянный коэффициент в знаменателях уравнений 7.17 и 7.18 должен быть равным 4 для шарнирных опор и 8 - для опор с заделкой концов.
При расчете максимально допустимого напряжения по отношению к пределу прочности материала направляющей на растяжение, следует принимать коэффициент запаса 5, что составляет практически половину значения, определенного для случая работы ловителя.

Горизонтальная упругая деформация в средней точке балки в двух взаимно перпендикулярных направлениях рассчитается по формулам:
Постоянный коэффициент в уравнениях 7.19 и 7.20 будет 48 для шарнир-
ных опор и 192 для опор с заделкой концов.
Максимально допустимые прогибы в соответствии с уравнениями 7.19 и
7.20 составляют 3 мм в плоскости направляющих (уу) и 6 мм в перпендикулярном направлении (ух).

Американский Стандарт Безопасности А 17.1
Метод расчетов, определенный в А17.1, непонятный, т.к. он основан на графиках для расчета размера направляющих без представления теоретического обоснования. Тем не менее, форма графиков аналогична форме графиков, основанных на Британских критериях и, в результате, предполагается, что исходные допущения и методы расчета сходны в обоих нормативных документах.

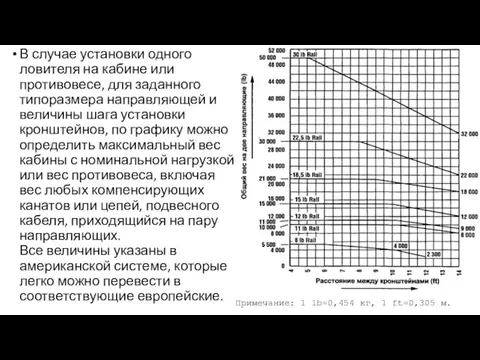
В случае установки одного ловителя на кабине или противовесе, для заданного типоразмера направляющей и величины шага установки кронштейнов, по графику можно определить максимальный вес кабины с номинальной нагрузкой или вес противовеса, включая вес любых компенсирующих канатов или цепей, подвесного кабеля, приходящийся на пару направляющих.
Все величины указаны в американской системе, которые легко можно перевести в соответствующие европейские.
Примечание: 1 lb=0,454 кг, 1 ft=0,305 м.

При применении двух ловителей кабины или противовеса (сдвоеных) нагрузки, определенные на предыдущем рис., могут быть увеличены с помощью множителей приведенных в табл. 7.6.

Там, где противовесы не оборудованы ловителем, вес противовеса на пару направляющих не должен превышать значений табл.7.7. Если не используется железобетон, расстояние между кронштейнами не должно превышать 4,88 м (16 фут).

В А17.1 определено максимальное напряжение в направляющей или ее креплении под действием горизонтальных сил, действующих на направляющую в процессе загрузки, разгрузки или перемещении, рассчитанное без ударной нагрузки как 103 Н/мм2, основанное на классе загрузки и максимально допустимом прогибе 6,3 мм.

Европейский Стандарт EN 81-1:1998
Методы вычислений, включенные в Приложение G этого стандарта, до-
вольно подробны и исключительно информативны и, соответственно, здесь обсуждаться не будут. Нормирован только коэффициент запаса, максимально допустимое напряжение и максимально допустимый прогиб.
В табл.7.8 приведены значения коэффициента запаса по отношению к
пределу прочности материала направляющих в зависимости от условий эксплуатации и относительного удлинения (пластичности) материала направляющей.
Материал с удлинением до 8% не может использоваться для направляющих.

В табл. 7.9 представлены максимально допустимое напряжение для наиболее распространенных величин предела прочности материала направляющей и для всех условий эксплуатации.
Максимально допустимый погиб направляющих профиля Т:
(a) 5 мм в обоих направлениях для направляющей при работе ловителя,
(b)10 мм для обоих направлений направляющих противовеса без лови-
телей.

7.2.4. Оценка методов расчета
Расчеты напряжений и прогибов, включенные в стандарт BS 5655:Part 9,
касаются всех условий эксплуатации. Однако могут возникнуть возражения при
проведении детального анализа.
В разделе 7.2.1 был представлен анализ напряжения направляющих, приводящему к заключению, что при воздействии ловителя направляющие никогда не подвергаются напряжению от комбинации продольного изгиба и изгиба в плоскости действия изгибающего момента, т.е. в направлении оси у-у площади поперечного сечения направляющей. Это было всегда сочетанием сжатия и изгиба. Поэтому неправильно рассматривать возможность одновременного действия продольного изгиба и изгиба в плоскости внешнего момента.

Однако напряжения продольного изгиба не следует игнорировать во избежание риска потери статической устойчивости направляющих.
Продольный изгиб может произойти в плоскости наименьшей изгибной
жесткости направляющей.
Нормативы для определения тормозной силы ловителя Fb могут стать предметом обсуждения, в частности, при применении ловителя резкого торможения. Ускорение торможения 40 м/с2 кажется довольно небольшим.
Предполагается, что нагрузка равномерно распространяется на полу кабины при работе ловителя.
Эффект одновременного действия тормозной силы ловителя и горизонтальных сил, вызванных эксцентричным положением груза в кабине, не принимаются во внимание.

В высшей степени невероятно совпадение работы ловителя и наиболее неблагоприятного распределение нагрузки на полу кабины для современных конструкций лифтов; однако эффект одновременности для панорамных лифтов, где консольная нагрузка всегда создает поперечные нагрузки направляющих, следует учитывать.
Поперечные силы могут быть также вызваны весом собственной массы кабины в зависимости от положения центра тяжести и точки подвески. Кроме того, из-за консольного положения нагрузки дополнительный динамический вращающий момент в ходе работы ловителя приведет к действию дополнительных динамических сил на направляющие.

В стандарте BS 5655:Part 9 регламентированы горизонтальные силы, действующие на направляющие в нормальных условиях эксплуатации, а также максимально допустимые прогибы.
К сожалению, одновременное действие в одной и той же точке направляющей двух взаимно перпендикулярных сил не принимается во внимание, хотя нагрузка может неравномерно распределяться одновременно в обоих направлениях.
При расчете сил в направлении оси х-х (см. рис.7.16), нагрузка предполагается симметрично расположенной относительно оси х-х и силы на обе направляющие - одинаковой величины.

Уравнения для напряжения и допустимого прогиба были получены для простой балки с определенной степенью ограничения подвижности в точках крепления. В результате, в формулах были заменены знаменатели. Однако направляющие фактически являются неразрезными балками, и будет интересно провести сравнительные расчеты для получения разных результатов.
Скручивание направляющих, вызванное горизонтальными силами в направлении оси х-х, не принимается во внимание в любом стандарте, хотя его влиянием пренебрегать не следует.
Как уже говорилось, расчет направляющих, включенный в А 17.1, непонятный и, соответственно, здесь коментироваться не будет.
Дальнейшая эволюция стандартизации расчетов должна привести к использованию сложных компьютерных программ, которые могут отражать фактические условия и учитывать все влияющие факторы.

7.2.5. Рекомендуемый метод расчета направляющих
Рекомендуемый метод должен быть простым, охватывать все эксплуатационные условия и отражать современное состояние знания.
А. Работа ловителя
I. Все лифты, кроме лифтов с эксцентричными направляющими или с консольной подвеской.
(а) Напряжение от изгиба и сжатия σ:

Изгибающий момент вызван эксцентрически расположенной тормозной силой Fb; внешний момент Fb ∙ е.
Расчет производится для неразрезной балки.
В уравнении 7.21 S - площадь поперечного сечения направляющей (мм2),
е - эксцентриситет тормозной силы Fb (мм), Wx - момент сопротивления изгибу относительно оси х-х (мм3).
Коэффициент С1 дается в таблице 7.10 и зависит от количества пролетов
неразрезной балки.
Тормозная сила во всех случаях рассчитывается по формуле:

Здесь К - масса кабины (кг), n - количество направляющих, gn - стандартное ускорение свободного падения (м/с2) и к1- коэффициент динамичности, зависящий от типа ловителя:
k1 = 5 для ловителей резкого торможения кроме типа с заклинивающим роликом,
k= 3 для ловителей резкого торможения с заклинивающим роликом,
k = 2 для ловителей плавного торможения.

(b) Напряжение продольного изгиба
В плоскости минимальной жесткости изгиба направляющей напряжение рассчитывается по формуле:
где ω — коэффициент продольного изгиба, данный в таблицах 7.11 и 7.12 для стали с пределом прочности 370 Н/мм2 и 520 Н/мм2,соответственно, как функция гибкости λ.

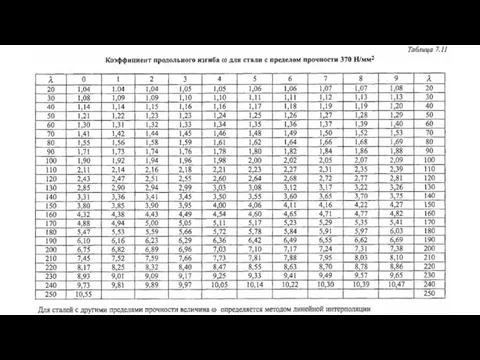
Для стали с пределом прочности 420 Н/мм2 коэффициент продольного изгиба может быть определен по формуле (линейная интерполяция):
Предполагается, что направляющая ведет себя как простая
балка с двумя опорами, нагруженная тормозной силой Fb, действующей в направлении её продольной оси.
Схема для расчета напряжений
продольного изгиба

Гибкость:
где i - радиус инерции, (мм),
где J- минимальный момент инерции площади поперечного сечения направляющей, (мм4), т.к. предполагается, что продольный изгиб происходит в плоскости наименьшей изгибной
жесткости направляющей.

В обоих случаях (а) и (Ь) максимально допускаемое напряжение должно соответствовать стандарту EN 81-1:1998.
Сравнительные расчеты, выполненные в Чешской Республике для ряда пассажирских и грузовых лифтов с разными основными параметрами, выявили, что определяющий вид напряжений зависит от показателя гибкости направляющей. Для гибкости λ ≤ 105 напряжение, вызванное совместным действием изгиба и сжатия, является определяющим, тогда как было доказано, что продольный изгиб ведет к критической ситуации в случае λ > 105.
Так как коэффициент продольного изгиба также в значительной степени зависит от материала направляющих, рекомендуется проводить расчет по обоим видам напряжений для гибкости 100-110.

II. Лифты с эксцентричным положением направляющих или с консольной подвеской
Следует проводить расчет суммарных напряжений при комбинированном действии изгиба и сжатия; дополнительно следует учитывать изгибающий момент, обусловленный наличием груза в кабине.
Нагрузка должна быть равномерно распределена на три четверти площади пола кабины в наиболее неблагоприятном положении.
Распределение нагрузки в широких кабинах (ширина больше глубины)
Распределение нагрузки вглубоких кабинах(глубина больше ширины)

Силы тяжести массы груза и кабины должны умножаться на коэффициент динамичности k1. Нагрузка должна быть приложена в соответствующей точке площади поперечного сечения.

В. Условия передвижения (нормальная работа)
Напряжение изгиба
Расположение боковых и поперечных сил, действующих на направляющие, показано на рис.

Предполагается, что нагрузка равномерно распределена на три четверти площади пола кабины в наиболее неблагоприятном положении.
Следует выполнить расчет напряжения изгиба для лифтов с эксцентричным расположением направляющих или с консольной подвеской.
Для типовых конструкций лифтов напряжение изгиба не велико.
Расчет будет выполнен для случая двухосного изгиба

Боковая сила:
Поперечная сила:
Максимальные изгибающие моменты можно получить из формул, если
h < 1,5 l (h - расстояние между центральными точками направляющих башмаков).

если h > 1,5l
Напряжение изгиба:
Если конфигурация отличается от показанной на рис. ранее, силы Fx и Fy должны быть рассчитаны соответствующим образом. Одновременное действие Fx и Fy происходит только в случае двуосного изгиба.

Прогиб
Прогиб в плоскости направляющих (у-у) рассчитывается по формуле:
где l - максимальное расстояние между центральными точками кронштейнов крепления пролета направляющей, (мм), Е- модуль упругости направляющей (Н/мм2), Jx - момент инерции площади поперечного сечения направляющей относительно оси х-х поперечного сечения (мм4).
С2 дано в табл. 7.13 и зависит от количества пролетов неразрезной балки.

Прогиб в плоскости х-х, перпендикулярной плоскости направляющих, может рассчитываться по формуле:
где Jy, - момент инерции площади поперечного сечения направляющей от-
носительно ocи y-y поперечного сечения (мм4).

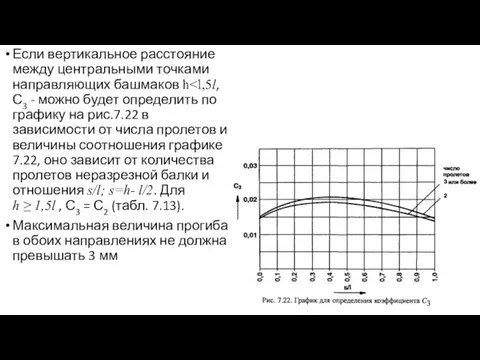
Если вертикальное расстояние между центральными точками направляющих башмаков h будет определить по графику на рис.7.22 в зависимости от числа пролетов и величины соотношения графике 7.22, оно зависит от количества пролетов неразрезной балки и отношения s/l; s=h- l/2. Для
h ≥ 1,5l , С3 = С2 (табл. 7.13).
Максимальная величина прогиба в обоих направлениях не должна превышать 3 мм

С. Загрузка (разгрузка)
Предполагается, что определенная часть номинальной нагрузки
Fs=f1Qgn действует на порог входа кабины.
Принимаются следующие значения величины f1
f1= 0,4 для пассажирских лифтов,
f1 = 0,75 для грузовых лифтов без загрузки вилочными погрузчиками
или подобными устройствами или, если в случае загрузки вилочными
Погрузчиками вес вилочного погрузчика включен в Q.
f1 = 1,25 для грузовых лифтов, если вес вилочного погрузчика не вклю-
чен в Q.
.

Основные формулы для одноосного изгиба (см. рис. ):
Поперечная сила нагрузки направляющей:
Изгибающий момент:
если h < 1,5 l,
если h > 1,5l,

Напряжение изгиба:
Прогиб:
С3 можно определить по графику на рис. 7.22.
В случае двухосного изгиба (т.е. где применяются двери одностороннего
открывания) - см. рис. 7.24.

В случае двухосного изгиба (т.е. где применяются двери одностороннего открывания) - см. рис. 7.24.