РавноускДвиж.СвободПадение

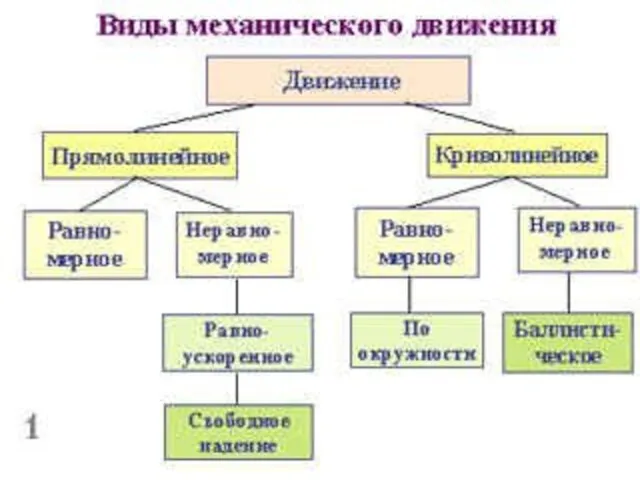
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ.
ДВИЖЕНИЕ
С УСКОРЕНИЕМ СВОБОДНОГО ПАДЕНИЯ

Что такое перемещение?
Что такое равномерное движение?
Что такое скорость равномерного прямолинейного движения?
Что такое средняя скорость?
Что такое мгновенная скорость?
это направленный отрезок, проведенный из начального положения тела в его конечное положение.
это такое движение, когда тело (материальная точка) за равные промежутки времени проходит равные пути.
это величина, равная отношению перемещения точки к промежутку времени, в течении которого это перемещение произошло.
это величина, равная отношению всего пути, пройденного телом, ко всему времени, за которое пройден этот путь.
это предел отношения перемещения
точки к промежутку времени , в течении которого это перемещение произошло при
.

Спортсмен пробежал дистанцию 400 м по дорожке стадиона и возвратился к месту старта. Определите путь L, пройденный спортсменом, и модуль его перемещения S.

Автомобиль двигался со скоростью 15 м/с в течение 5 с. Какой путь он проехал за это время?

Расчет скорости
Формула для расчета скорости в векторном виде:
Формула для расчета скорости в координатном виде:

Перемещение
Перемещение это векторная величина.
Формула для расчета перемещения:
Формула для расчета перемещения в векторной форме:

Еще одна формула для расчета перемещения при равноускоренном движении:

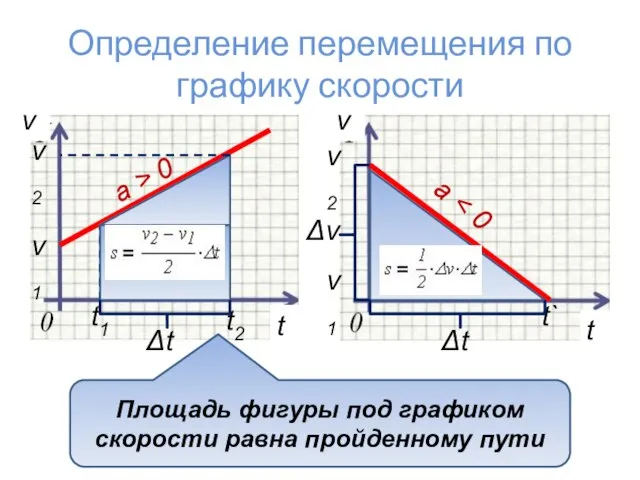
Определение перемещения по графику скорости
a < 0
a > 0
v1
t1
v2
v1
t
t
v
v
v2
t`
t2
Δt
Δt
Δv
Площадь фигуры под графиком скорости равна пройденному пути

Средняя скорость при прямолинейном движении c постоянным ускорением
Если при прямолинейном движении с постоянным ускорением направление скорости не меняется, то средний модуль скорости равен полусумме модулей начальной и конечной скоростей:
Связь между проекциями начальной и конечной скоростей, ускорения и перемещения

Уравнение движения
Формула уравнения движения в координатном виде:

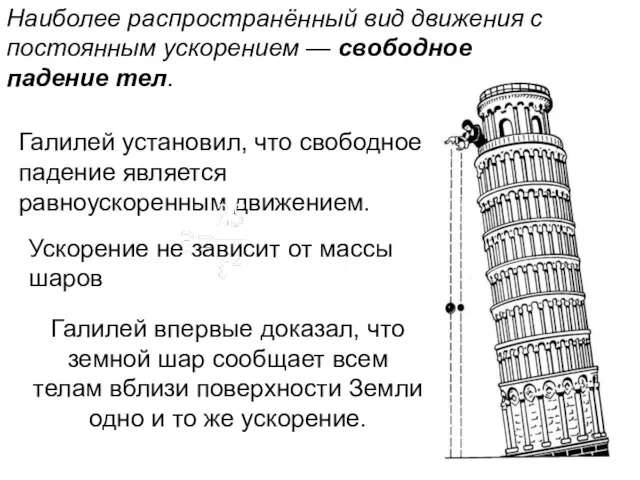
Наиболее распространённый вид движения с постоянным ускорением — свободное падение тел.
Галилей установил, что свободное падение является равноускоренным движением.
Ускорение не зависит от массы шаров
Галилей впервые доказал, что земной шар сообщает всем телам вблизи поверхности Земли одно и то же ускорение.

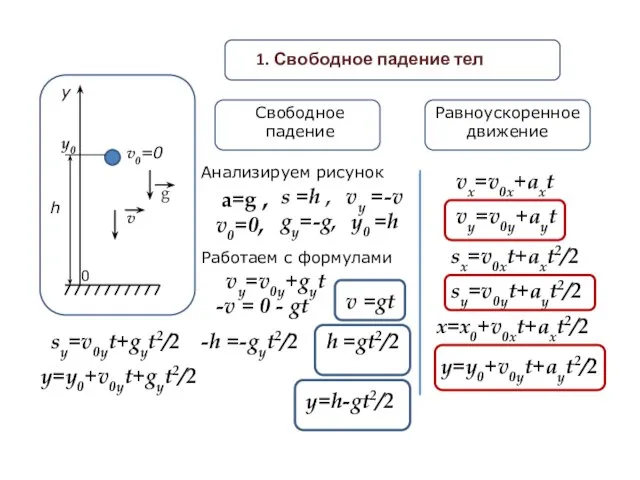
у
h
g
v0=0
1. Свободное падение тел
Равноускоренное
движение
Свободное
падение
vx=v0x+axt
vy=v0y+ayt
sy=v0yt+ayt2/2
sx=v0xt+axt2/2
x=x0+v0xt+axt2/2
y=y0+v0yt+ayt2/2
Анализируем рисунок
v0=0,
a=g ,
gy=-g,
y0 =h
Работаем с формулами
vy=v0y+gyt
sy=v0yt+gyt2/2
v
-v = 0 - gt
-h =-gyt2/2
y=y0+v0yt+gyt2/2
y=y0-gt2/2
v =gt
h =gt2/2
y=h-gt2/2
s =h ,
0
y0
vу =-v

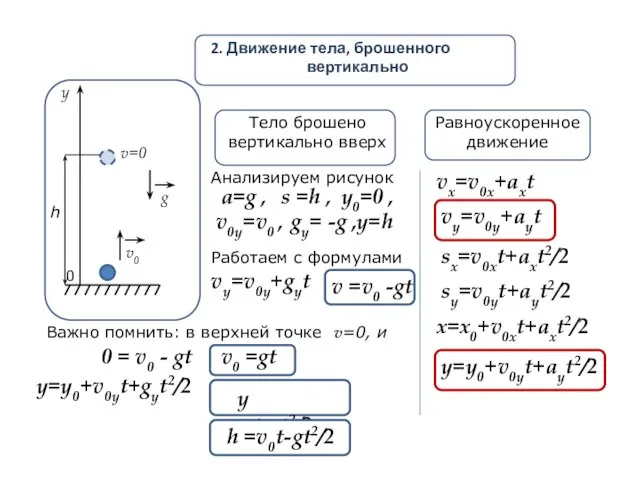
у
g
v=0
v0
h
2. Движение тела, брошенного
вертикально
Равноускоренное
движение
vx=v0x+axt
vy=v0y+ayt
sy=v0yt+ayt2/2
sx=v0xt+axt2/2
x=x0+v0xt+axt2/2
Тело брошено вертикально вверх
v0y=v0 ,
a=g ,
gy= -g ,
y=h
s =h ,
Анализируем рисунок
y0=0 ,
Работаем с формулами
0
vy=v0y+gyt
v =v0 -gt
Важно помнить: в верхней точке v=0, и
0 = v0 - gt
v0 =gt
y=y0+v0yt+gyt2/2
y =v0t-gt2/2
h =v0t-gt2/2
y=y0+v0yt+ayt2/2

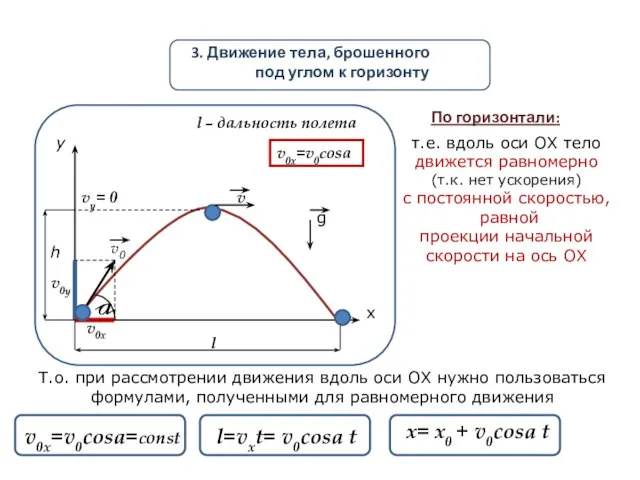
3. Движение тела, брошенного
под углом к горизонту
у
х
a
v0x
v0y
v0
v
vy= 0
l
h
g
По горизонтали:
т.е. вдоль оси ОХ тело
движется равномерно
(т.к. нет ускорения)
с постоянной скоростью,
равной
проекции начальной
скорости на ось ОХ
Т.о. при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения
l=vxt= v0cosa t
x= x0 + v0cosa t
l – дальность полета
v0x=v0cosa
v0x=v0cosa=const

v0x=v0cosa
у
х
a
v0x
v0y
v0
v
vy=0
l
h
g
По вертикали:
Вдоль оси ОУ тело
движется равнозамедленно,
подобно телу, брошенному вертикально вверх
со скоростью, равной проекции начальной скорости на ось ОУ
h - максимальная высота
v0у=v0sina
Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали
gy= -g ,
v0у=v0sina
=v0sina - gt
vy= v0y+gyt
y=y0+v0yt+gyt2/2 = v0sinat- gt2/2
=v0sina - gt

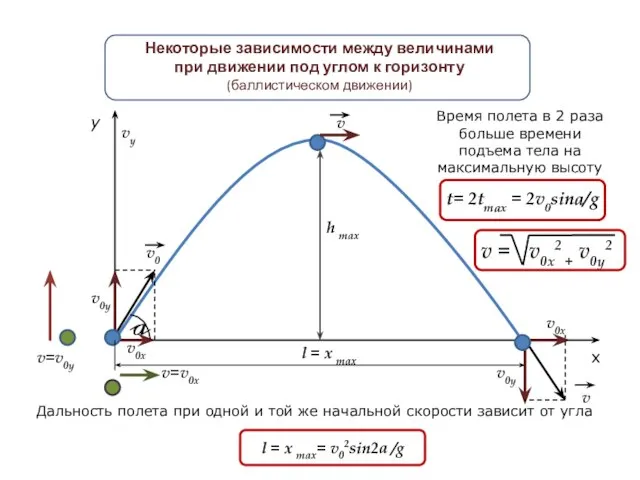
h max
y
x
v0у
v0х
v0у
vу
v0х
v
v0
a
v=v0у
v
v=v0x
Некоторые зависимости между величинами
при движении под углом к горизонту
(баллистическом движении)
Время полета в 2 раза
больше времени
подъема тела на
максимальную высоту
t= 2tmax = 2v0sina/g
Дальность полета при одной и той же начальной скорости зависит от угла
l = x max= v02sin2a /g
v =
+ v0у2
v0x2
l = x max

Движение с постоянным ускорением свободного падения
Так как ускорение свободного падения с течением времени не меняется, то движение тела в данном случае, как и любое движение с постоянным ускорением, можно описать уравнениями
υ0x = υ0cosα, υ0y= υ0sinα, ax = 0 и ay = -g.
Проекции вектора на оси координат:

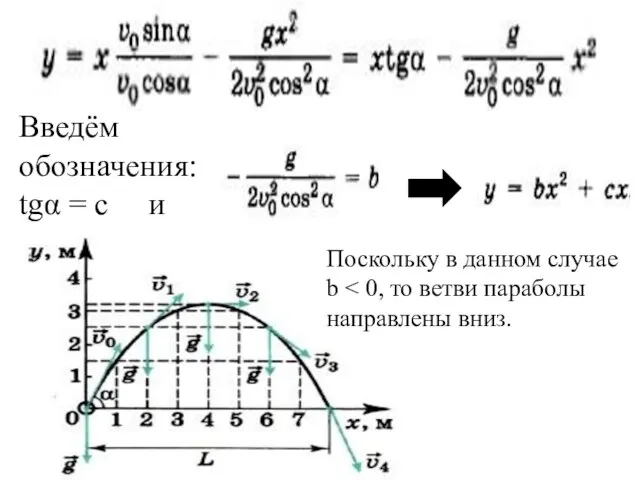
Введём обозначения: tgα = с и
Поскольку в данном случае b < 0, то ветви параболы направлены вниз.

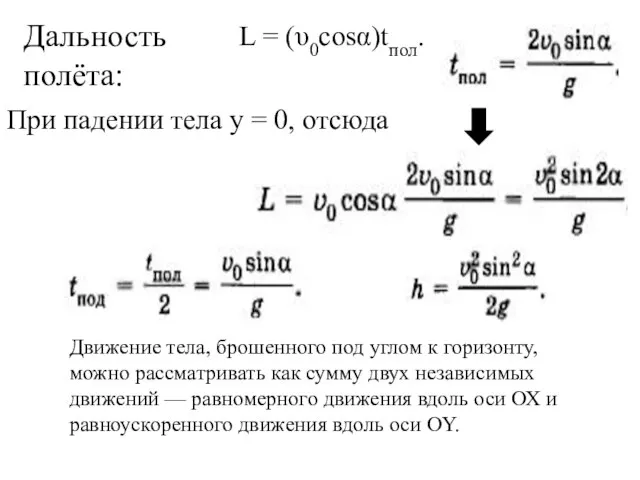
Дальность полёта:
При падении тела у = 0, отсюда
L = (υ0cosα)tпол.
Движение тела, брошенного под углом к горизонту, можно рассматривать как сумму двух независимых движений — равномерного движения вдоль оси ОХ и равноускоренного движения вдоль оси OY.

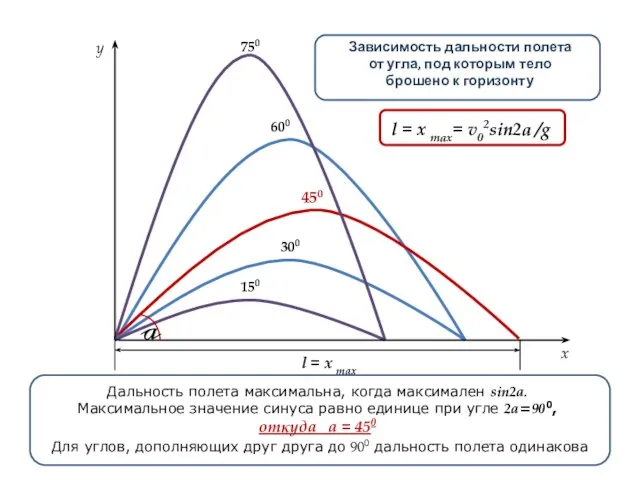
150
750
450
300
600
y
x
v0x=v0cosa
Зависимость дальности полета
от угла, под которым тело
брошено к горизонту
l = x max
l = x max= v02sin2a /g
a
v0x=v0cosa
Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=900,
откуда a = 450
Для углов, дополняющих друг друга до 900 дальность полета одинакова

4. Движение тела, брошенного
горизонтально
v0у=0,
a=g ,
gy= -g ,
y0 =h
s =h ,
Анализируем рисунок:
По горизонтали:
тело движется равномерно
с постоянной скоростью, равной проекции начальной скорости на ось ОХ
v0x= v0
l=vxt= v0cosa t
l=v0xt= v0 t
По вертикали:
Тело свободно падает с высоты h .
Именно поэтому, применимы формулы для свободного падения:
v =gt
h =gt2/2
y=y0-gt2/2
v0
g
h
l
v0y=0
v0x
у
х

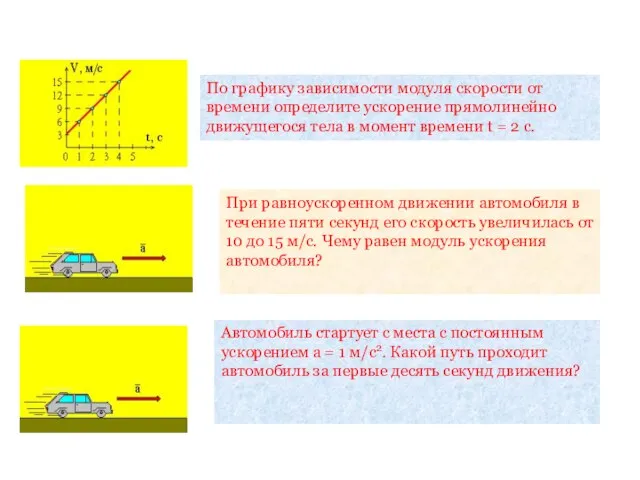
По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени t = 2 с.
При равноускоренном движении автомобиля в течение пяти секунд его скорость увеличилась от 10 до 15 м/с. Чему равен модуль ускорения автомобиля?
Автомобиль стартует с места с постоянным ускорением а = 1 м/с2. Какой путь проходит автомобиль за первые десять секунд движения?

Маленький стальной шарик упал с высоты 45 м. Сколько времени длилось его падение? Какое перемещение совершил шарик за первую и последнюю секунды своего движения?

С какой высоты свободно падала сосулька, если расстояние до земли она преодолела за 4 с?