Содержание
- 2. Кинематика твердого тела Задать движение твердого тела – значит, указать способ определения положения каждой точки в
- 3. Виды движения твердого тела Поступательное движение Вращательное движение Плоско-параллельное движение Сферическое движение Общий случай движения твердого
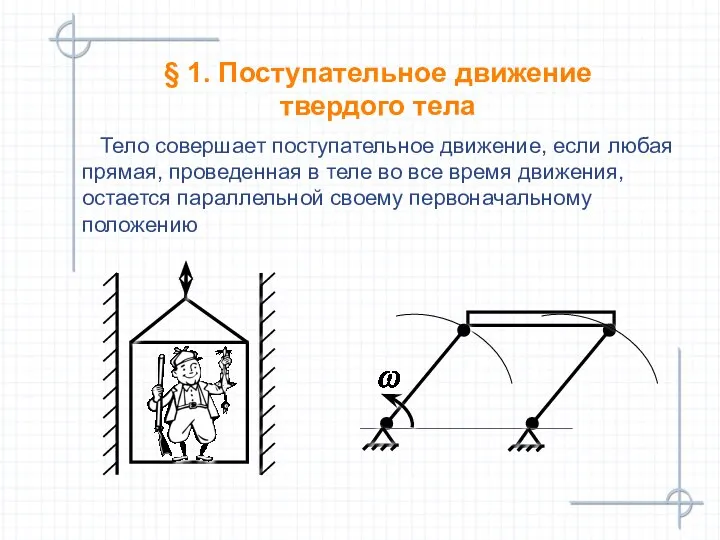
- 4. § 1. Поступательное движение твердого тела Тело совершает поступательное движение, если любая прямая, проведенная в теле
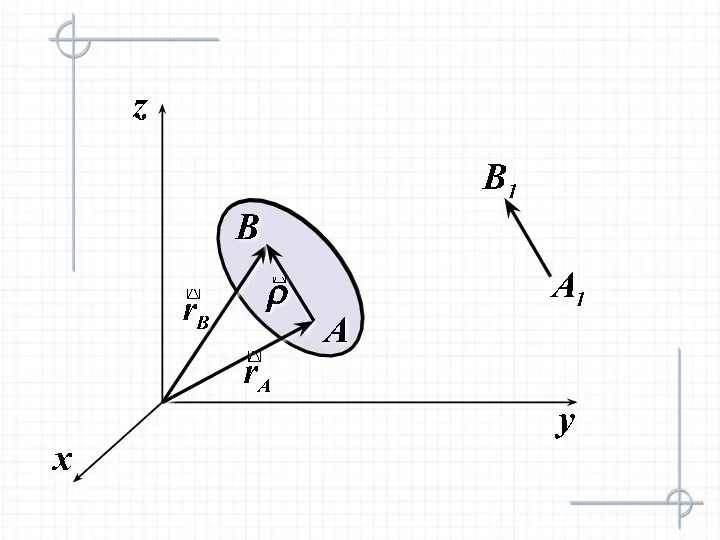
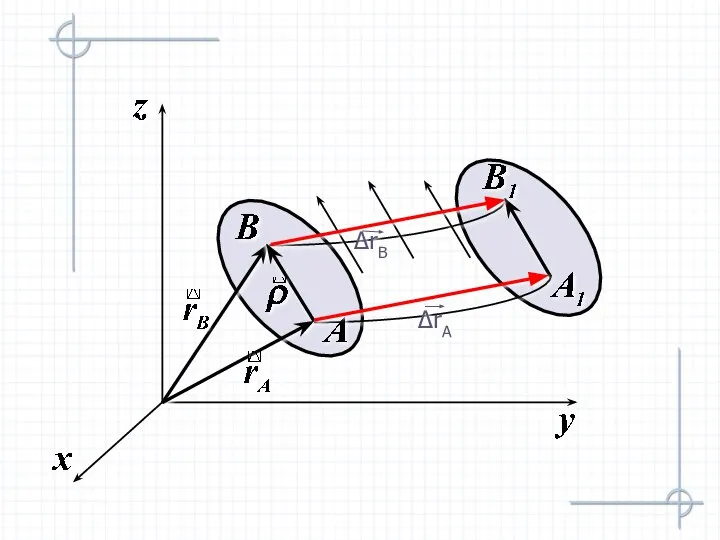
- 5. Теорема, определяющая свойства поступательного движения При поступательном движении твердого тела все его точки описывают одинаковые траектории
- 9. Найдем скорости точек А и В
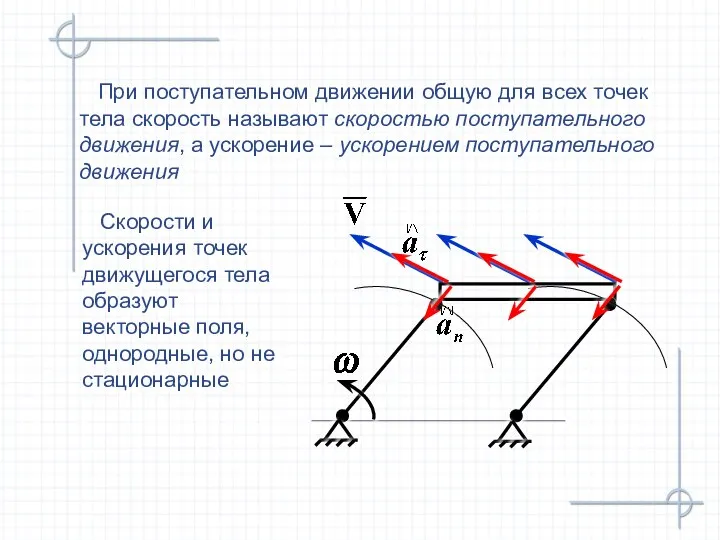
- 12. При поступательном движении общую для всех точек тела скорость называют скоростью поступательного движения, а ускорение –
- 13. § 2. Вращательное движение твердого тела вокруг неподвижной оси Движение твердого тела с двумя неподвижными точками
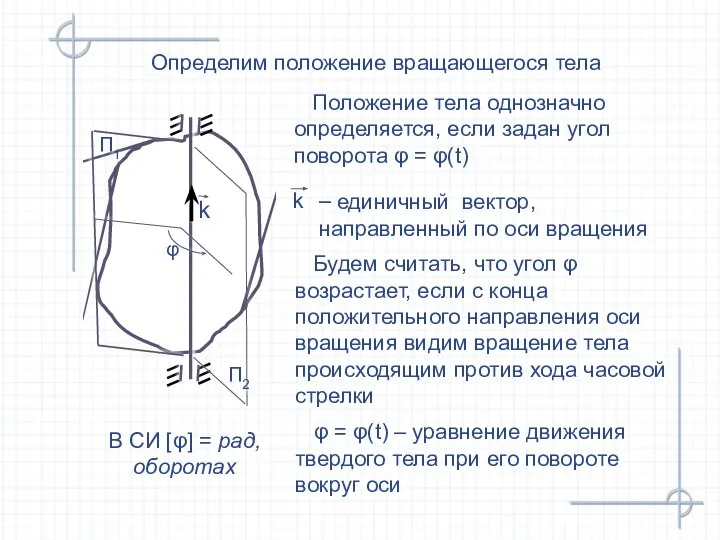
- 14. Положение тела однозначно определяется, если задан угол поворота φ = φ(t) Определим положение вращающегося тела П2
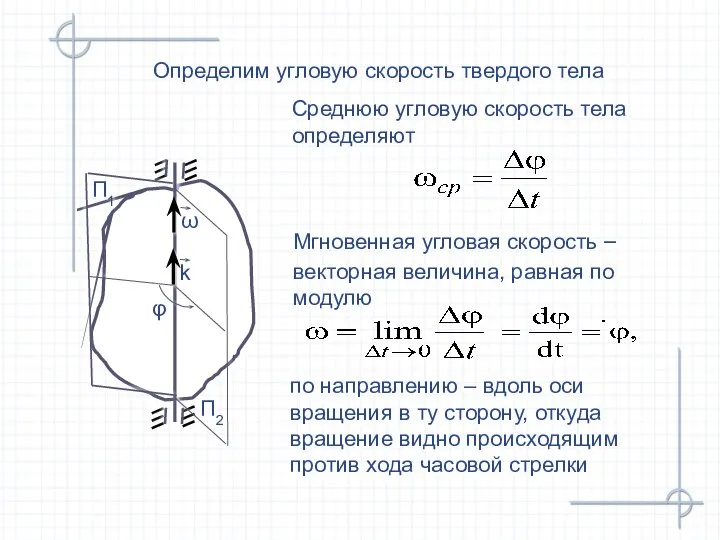
- 15. Среднюю угловую скорость тела определяют Определим угловую скорость твердого тела П2 П1 Мгновенная угловая скорость –
- 16. В технике при равномерном вращении пользуются n – числом оборотов в минуту В системе СИ [ω]
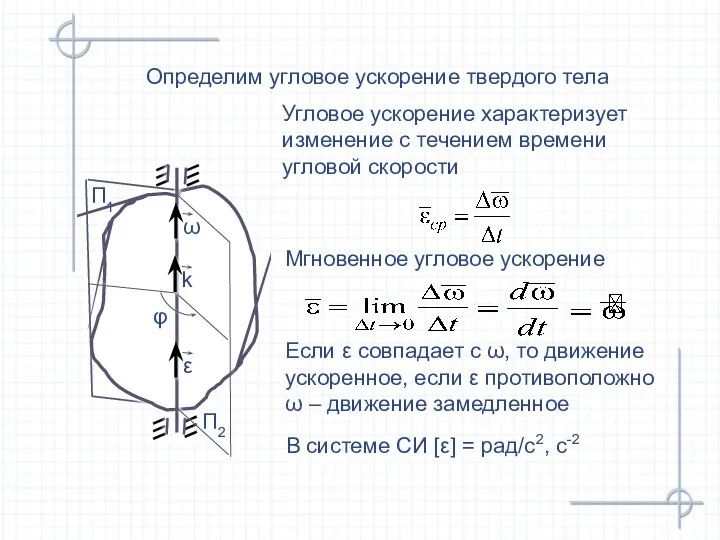
- 17. Угловое ускорение характеризует изменение с течением времени угловой скорости Определим угловое ускорение твердого тела П2 П1
- 18. Равномерное вращение Если то вращение называется равномерным Закон равномерного вращения твердого тела С – константа интегрирования
- 19. Равнопеременное вращение Если ω и ε имеют одинаковые знаки, то вращение равноускоренное, если разные – равнозамедленное
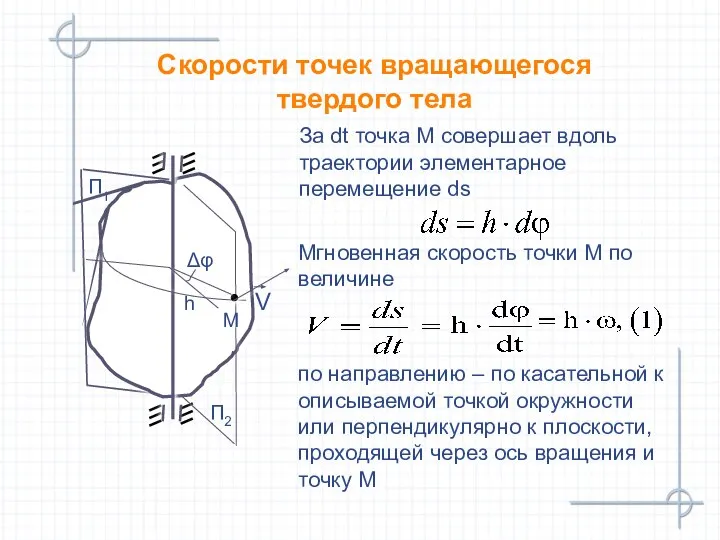
- 20. За dt точка М совершает вдоль траектории элементарное перемещение ds Скорости точек вращающегося твердого тела П2
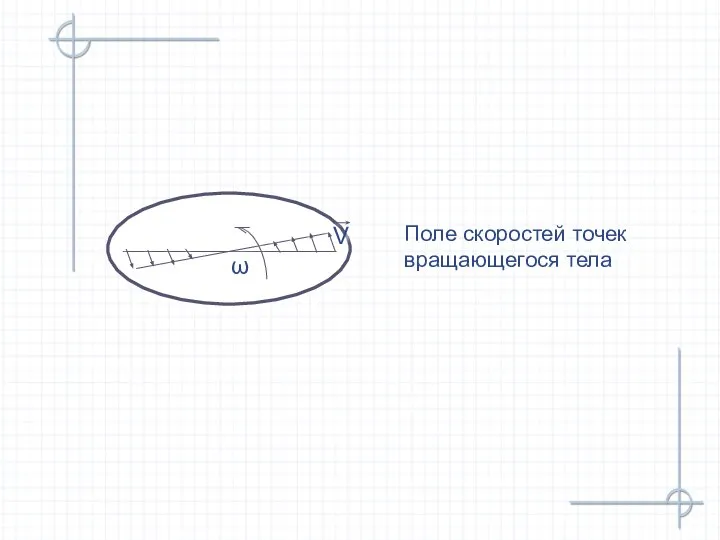
- 21. Поле скоростей точек вращающегося тела
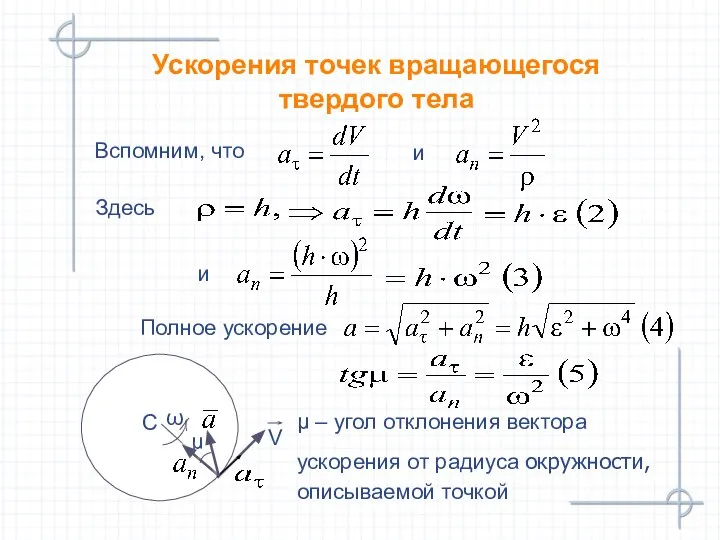
- 22. Вспомним, что Ускорения точек вращающегося твердого тела μ Здесь Полное ускорение и и C μ –
- 23. Поле ускорений точек вращающегося тела Формулы (1)–(5) позволяют определить скорость и ускорение любой точки вращающегося тела,
- 24. Леонард Эйлер (1707 –1783) показал, что скорость вращающейся точки тела можно определить из векторного произведения угловой
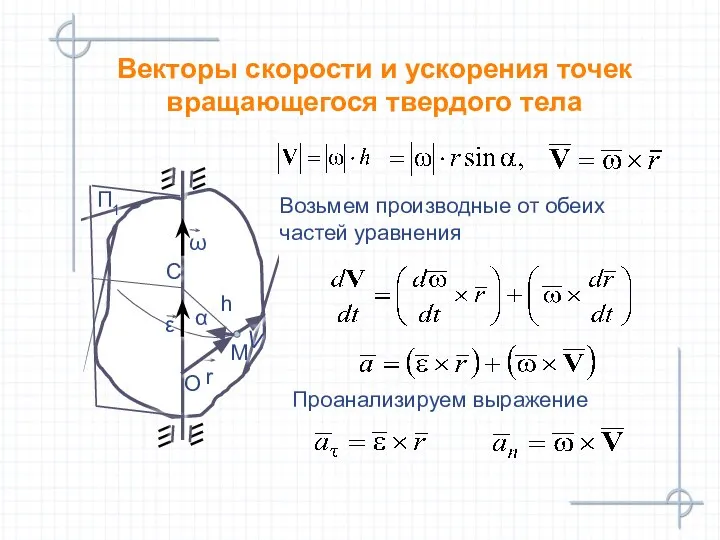
- 25. Векторы скорости и ускорения точек вращающегося твердого тела П1 С Возьмем производные от обеих частей уравнения
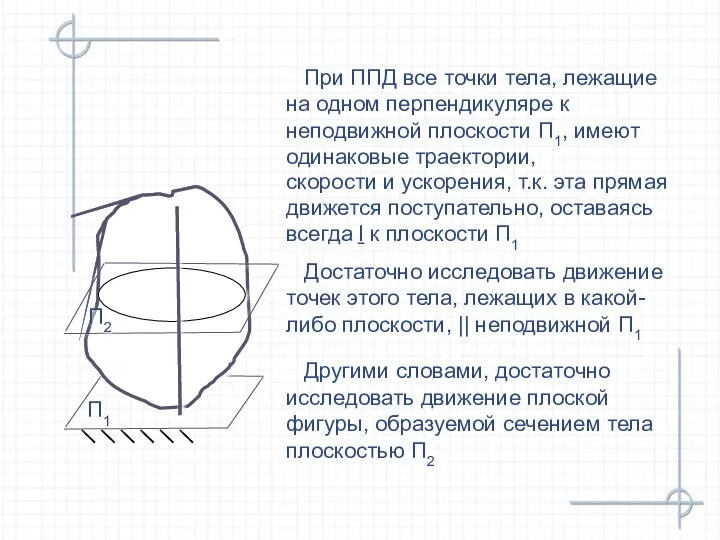
- 26. § 3. Плоско-параллельное движение твердого тела Плоско-параллельным (или плоским) движением (ППД) твердого тела называется такое, при
- 27. скорости и ускорения, т.к. эта прямая движется поступательно, оставаясь всегда ḻ к плоскости П1 При ППД
- 28. Положение фигуры в плоскости П2 по отношению к неподвижной системе координат ОХУ определяется положением какого-либо отрезка
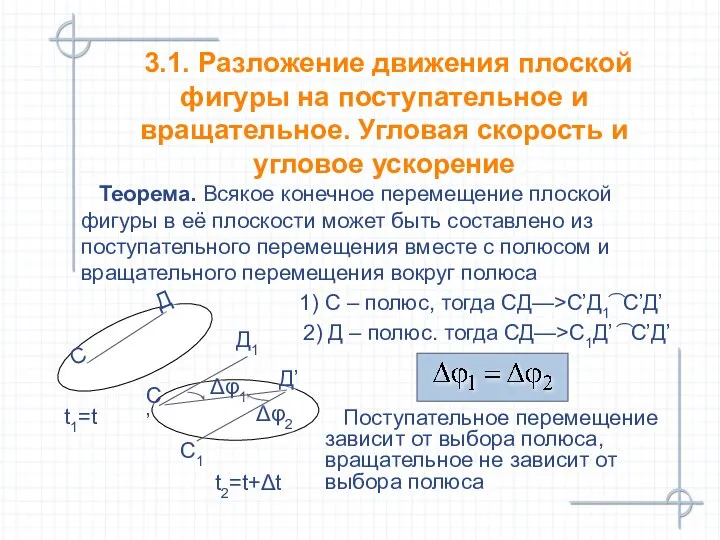
- 29. Теорема. Всякое конечное перемещение плоской фигуры в её плоскости может быть составлено из поступательного перемещения вместе
- 30. Для характеристики вращательного движения вокруг подвижной оси, проходящей через полюс, введем понятия угловой скорости ω и
- 31. А – полюс; М – произвольная точка плоской фигуры; 3.2. Определение траекторий и скоростей точек плоской
- 32. Скорости точек плоской фигуры (4) Скорость любой точки М плоской фигуры равна геометрической сумме скоростей какой-либо
- 33. (5) Вращательная скорость VMA определяется численно и по направлению так же, как если бы тело совершало
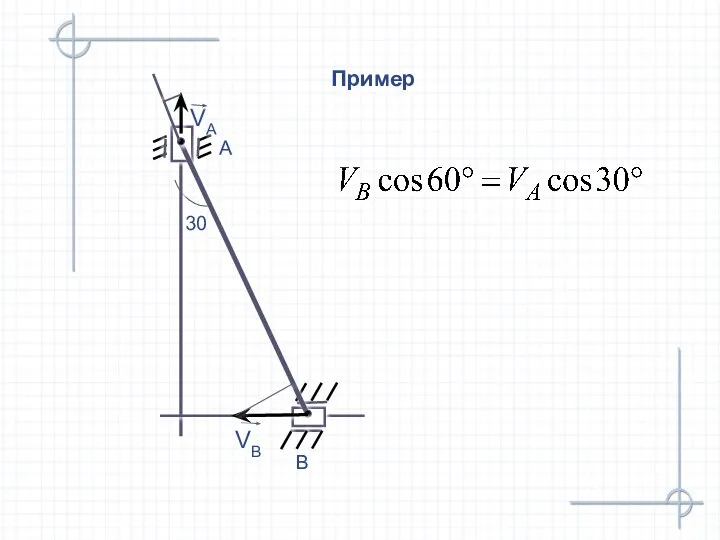
- 34. (6) 3.3. Теорема о проекциях скоростей Найдем скорость точки В. Пусть точка А – полюс При
- 35. Пример B A
- 36. 3.4. Мгновенный центр скоростей (мцс) Мгновенный центр скоростей (мцс) – это такая точка плоской фигуры, скорость
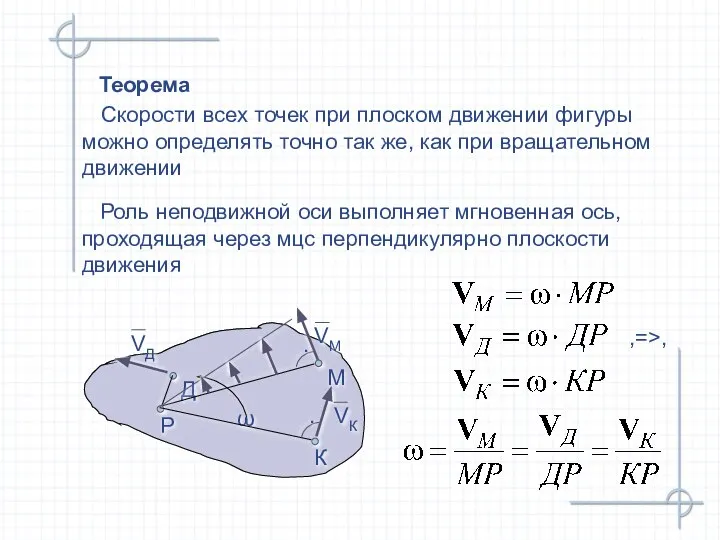
- 37. Теорема Скорости всех точек при плоском движении фигуры можно определять точно так же, как при вращательном
- 38. Выводы 1. Для определения мцс надо знать только направление скоростей двух каких-нибудь точек плоской фигуры (или
- 39. 3. Угловая скорость плоской фигуры в каждый момент времени равна отношению скорости какой-нибудь точки фигуры к
- 40. 3.5. Частные случаи определения МЦС 1. Интуитивный Точка соприкосновения неподвижной поверхности и катящегося без скольжения диска
- 41. (·)Р – МЦС (·)А и (·)К принадлежат II колесу, => Свойство пропорции Если VA || VK
- 42. 3. Случай мгновенно поступательного движения 4. Если известна скорость какой-либо (·)В и угловая скорость тела, то
- 43. 3.6. Определение ускорений точек при ППД (7) продифференцируем
- 44. Пример. Два колеса соединены водилом ОА. I-е колесо вращается с угловой скоростью ωI относительно неподвижного шарнира
- 45. Можем найти линейное ускорение любой точки колеса II О А K где
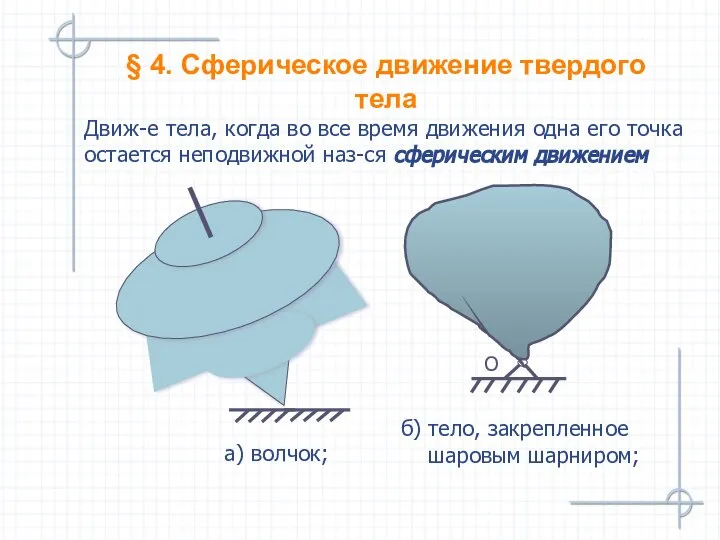
- 46. § 4. Сферическое движение твердого тела б) тело, закрепленное шаровым шарниром; Движ-е тела, когда во все
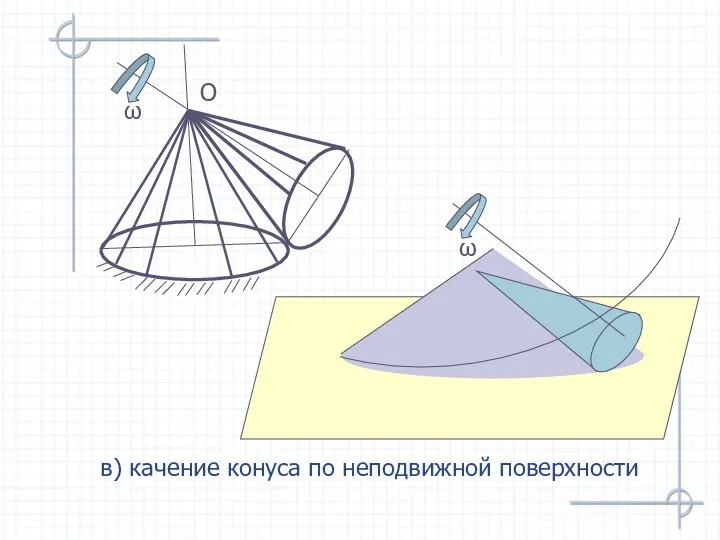
- 47. в) качение конуса по неподвижной поверхности
- 48. Линия ОК – линия узлов. а) Уравнения движения: Положение тела отн-но неподви-жных осей ОX1Y1Z1 можно определить
- 49. Линия ОК – линия узлов. б) угловая скорость тела: - собственное вращение вокруг оси z -
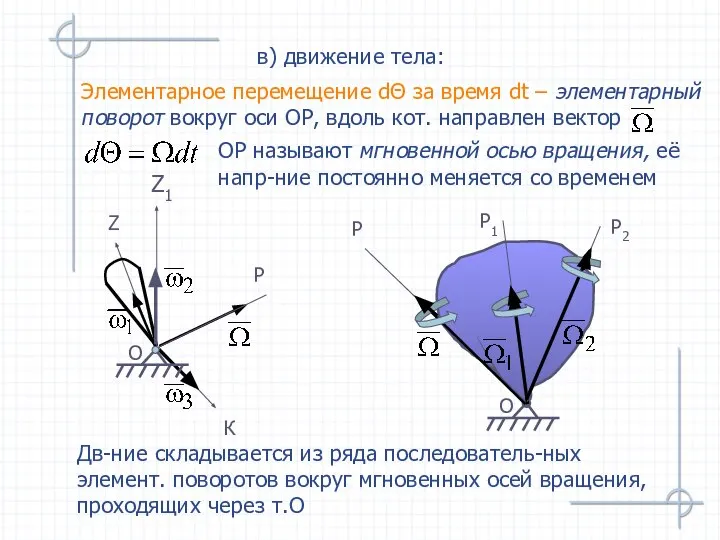
- 50. Элементарное перемещение dΘ за время dt – элементарный поворот вокруг оси ОР, вдоль кот. направлен вектор
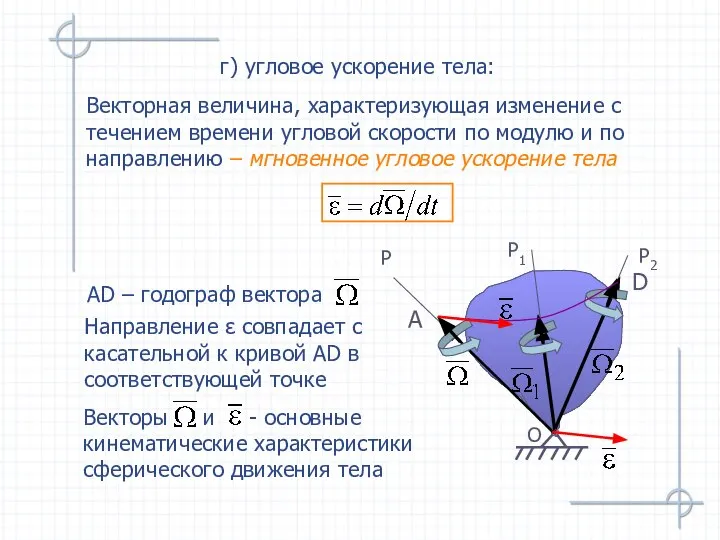
- 51. г) угловое ускорение тела: Направление ε совпадает с касательной к кривой АD в соответствующей точке АD
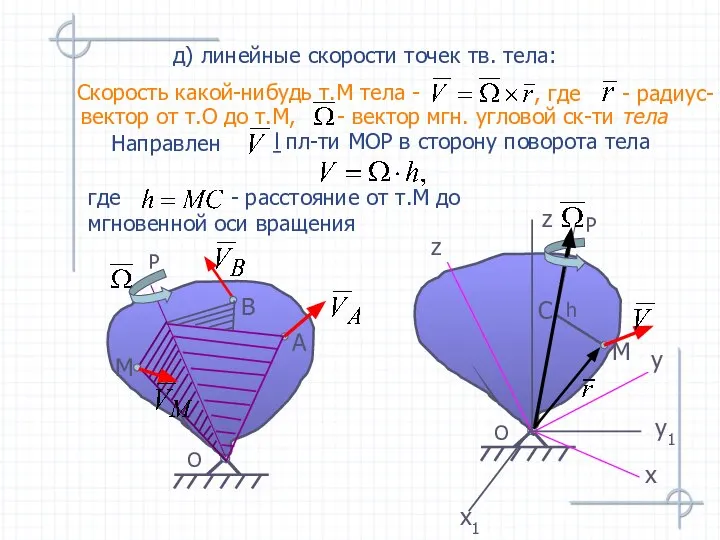
- 52. вектор от т.О до т.М, - вектор мгн. угловой ск-ти тела д) линейные скорости точек тв.
- 53. - вращательное ускорение е) линейные ускорения точек тв. тела: Ускорение какой-нибудь т.М тела - или С
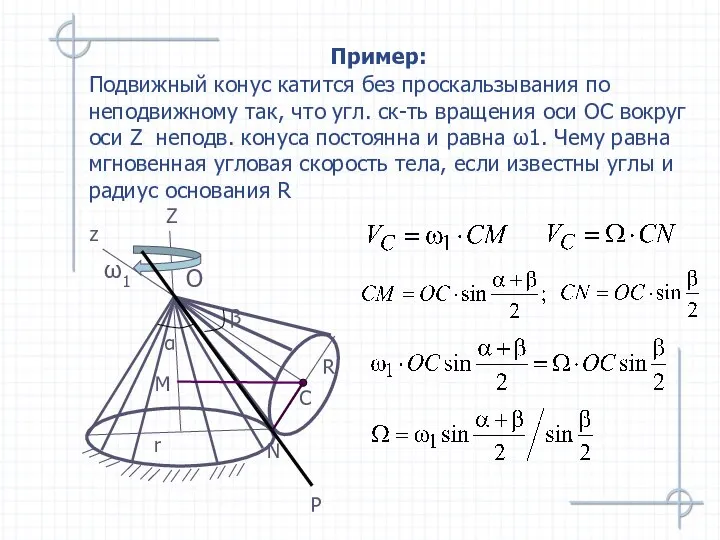
- 54. Пример: Подвижный конус катится без проскальзывания по неподвижному так, что угл. ск-ть вращения оси ОС вокруг
- 55. А § 5. Общий случай движения свободного твердого тела (4) – уравнения свободного движения твёрдого тела
- 56. Движение свободного твердого тела в общем случае можно рассматривать как совокупность поступательного движения вместе с точкой
- 58. Скачать презентацию




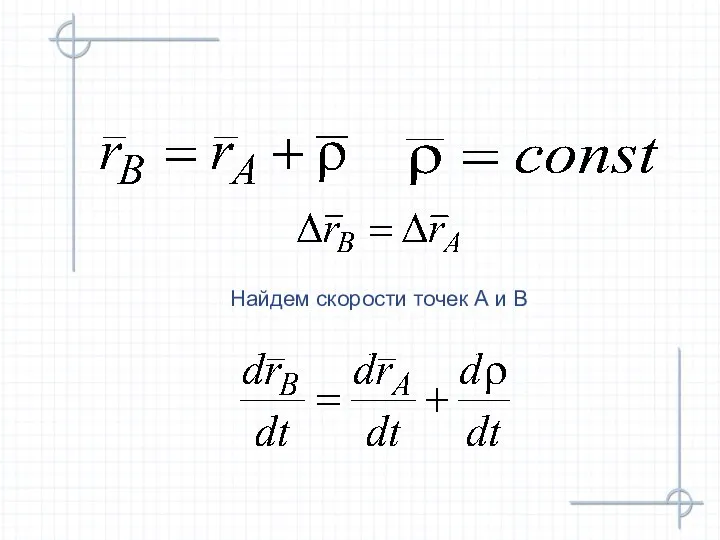
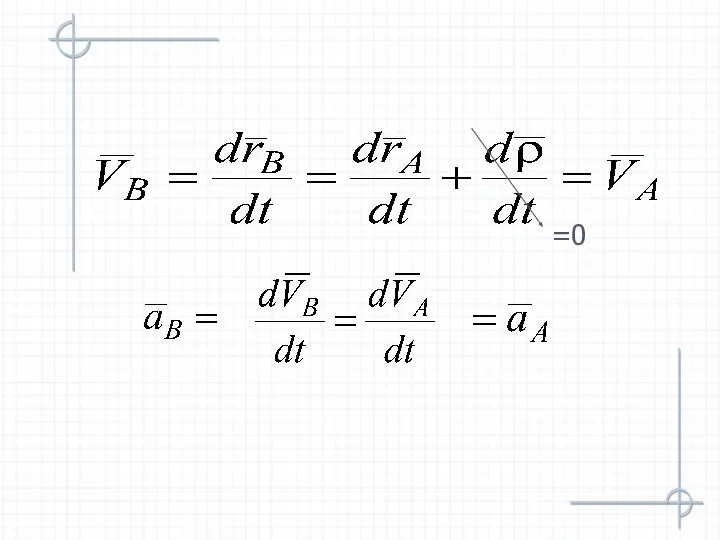
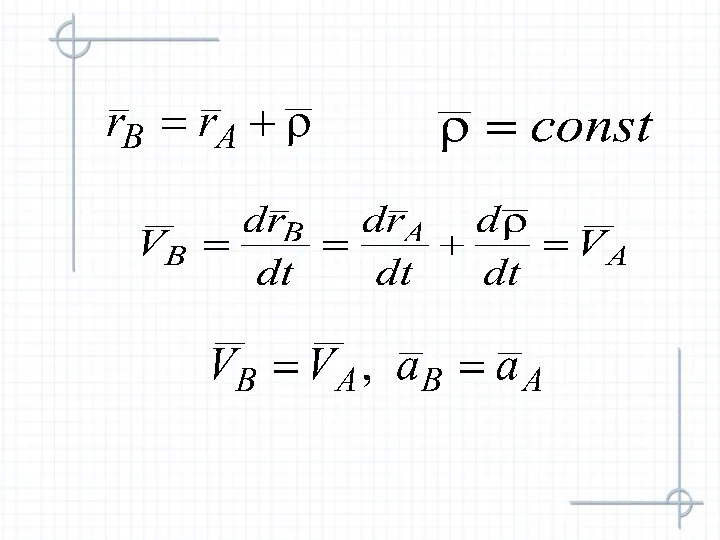



























 История нанотехнологий. Лекция 2
История нанотехнологий. Лекция 2 Электрическое поле
Электрическое поле Коллективные спасательные средства. Тема 2.3
Коллективные спасательные средства. Тема 2.3 Повышение качества преподавания физики
Повышение качества преподавания физики Двойные интегралы
Двойные интегралы Использование инновационных технологий для повышения мотивации обучения физики
Использование инновационных технологий для повышения мотивации обучения физики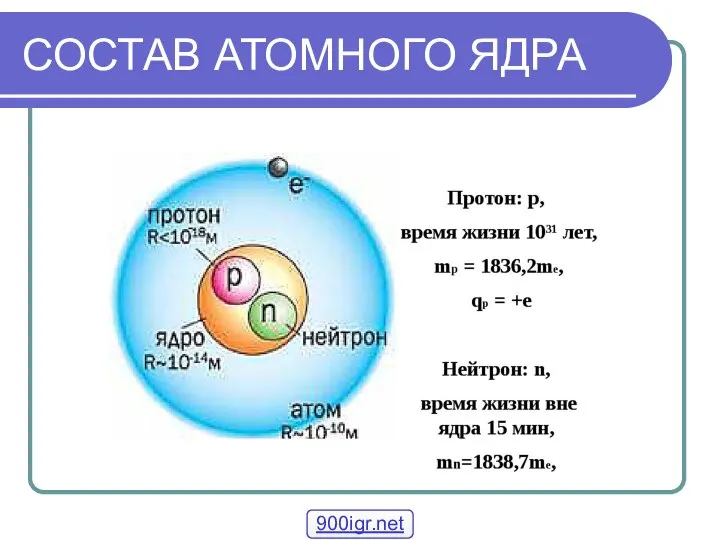 Состав атомного ядра
Состав атомного ядра Необычные барометры
Необычные барометры Физические методы анализа Метод красок и ультразвуковой метод анализа на выявление структуры
Физические методы анализа Метод красок и ультразвуковой метод анализа на выявление структуры Прямолинейное равномерное и прямолинейное равноускоренное движения
Прямолинейное равномерное и прямолинейное равноускоренное движения Расчет электрических цепей переменного тока. Лекция 4
Расчет электрических цепей переменного тока. Лекция 4 Диэлектрики в энергетическом поле
Диэлектрики в энергетическом поле Презентация на тему Радиация: проблемы и перспективы
Презентация на тему Радиация: проблемы и перспективы  Теоретическая механика
Теоретическая механика Фотометрия и светотехника (Тема 1)
Фотометрия и светотехника (Тема 1) Руководство для выполнения графических работ. Начертательная геометрия
Руководство для выполнения графических работ. Начертательная геометрия Закон Джоуля-Ленца
Закон Джоуля-Ленца Методы зубонарезания
Методы зубонарезания Поршневой компрессор. Лабораторная работа
Поршневой компрессор. Лабораторная работа Давление твёрдых тел, жидкостей и газов
Давление твёрдых тел, жидкостей и газов Газоразрядные приборы
Газоразрядные приборы Презентация на тему Гелиоцентрическая система Николая Коперника
Презентация на тему Гелиоцентрическая система Николая Коперника  Законы проведения возбуждения по нервному волокну. Парабиоз. Физиологические свойства синапсов
Законы проведения возбуждения по нервному волокну. Парабиоз. Физиологические свойства синапсов Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза  Информационно - коммуникационные технологии на уроках физики
Информационно - коммуникационные технологии на уроках физики Атомное ядро
Атомное ядро Презентация на тему Физика в космосе
Презентация на тему Физика в космосе  Основные представления о напряженном состоянии горных пород
Основные представления о напряженном состоянии горных пород