Содержание
- 2. Для решения задач динамики с учетом упругости звеньев прибегают к приближенному решению, когда машину или исследуемый
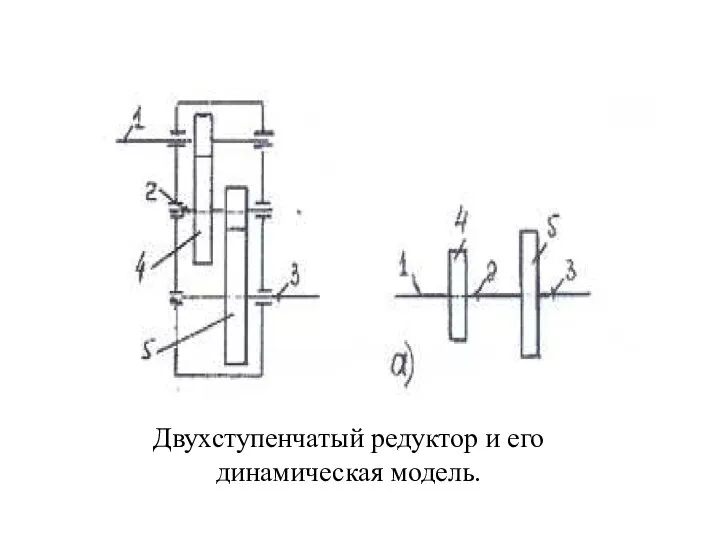
- 3. Двухступенчатый редуктор и его динамическая модель.
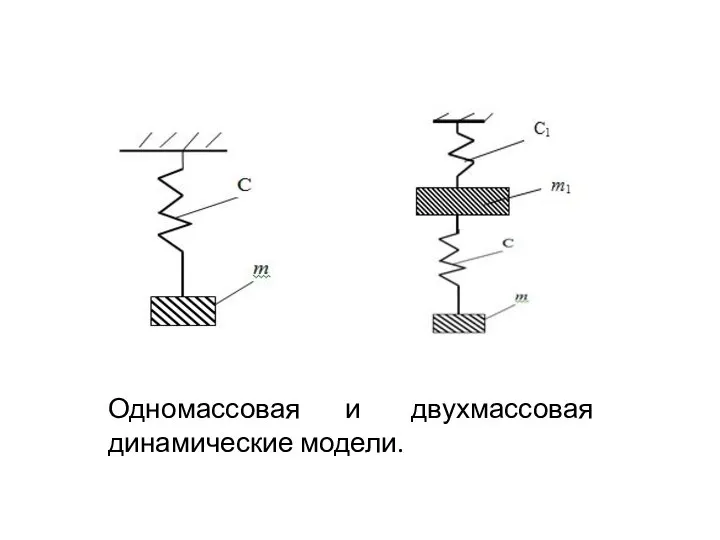
- 4. Одномассовая и двухмассовая динамические модели.
- 5. При решении задач с учетом сил упругого сопротивления звеньев механизмов следует учесть, что на тело, кроме
- 6. Учитывая изложенные выше зависимости и принятые допущения, получаем уравнение движения масс с учетом сил упругости или,
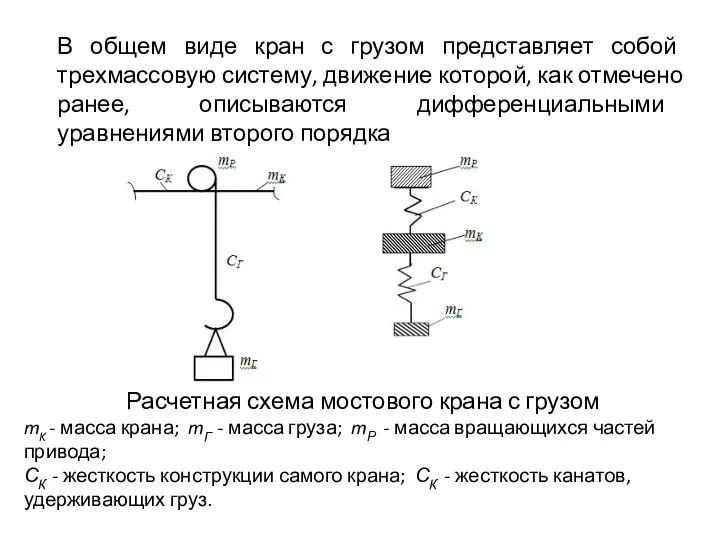
- 7. В общем виде кран с грузом представляет собой трехмассовую систему, движение которой, как отмечено ранее, описываются
- 8. Динамическая нагрузка при подъеме груза В процессе подъема возможны два варианта: подъем «с веса» и подъем
- 9. В начальный момент подъема нагрузка на грузозахватное устройство РГЗ составит РГЗ = QГ + Рдин ≥
- 10. Во втором случае – подъем «с подхватом» груз лежит на каком-либо основании, канаты провисают, и в
- 11. Динамическая нагрузка, также как в первом случае, зависит от жесткости опорной конструкции СК , но при
- 12. В первом случае – подъем «с веса» динамическая деформация самого крана мало отличается от статической. Поэтому
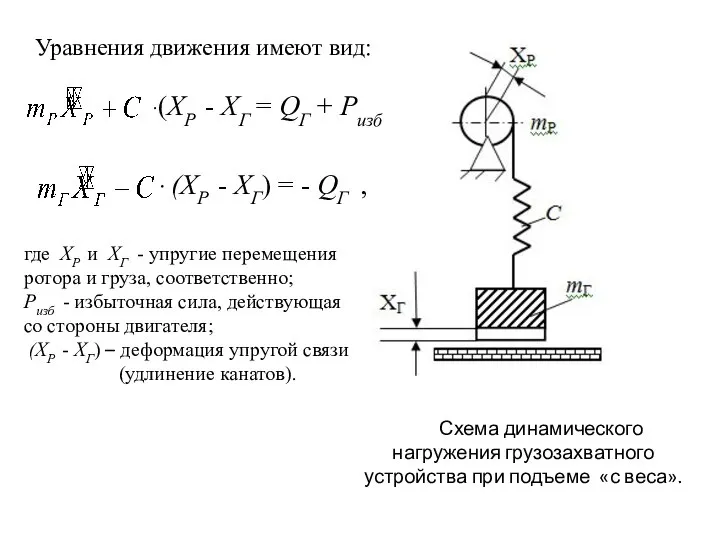
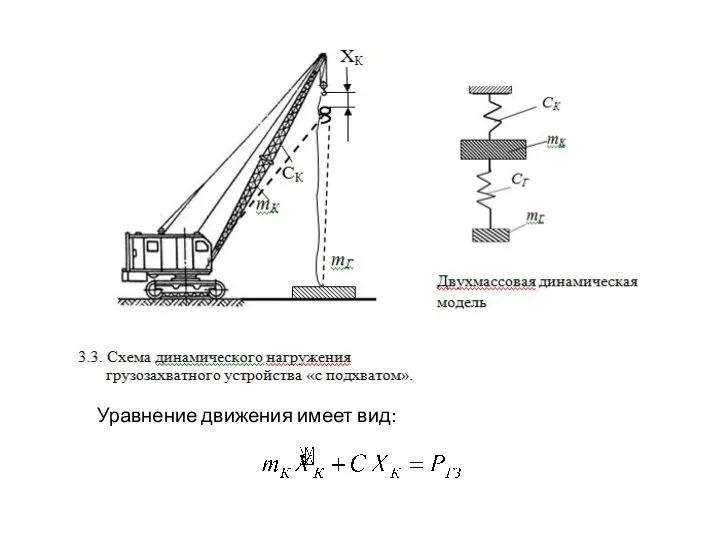
- 13. Схема динамического нагружения грузозахватного устройства при подъеме «с веса». ∙(ХР - ХГ = QГ + Ризб
- 14. Избыточную силу, действующая со стороны двигателя, определяют зависимостью Ризб = φ∙QГ (3.4) где φ = коэффициент
- 15. При торможении опускающегося груза величину Рдин и коэффициент динамичности определяют по тем же формулам, но под
- 16. Во втором случае – подъем «с подхватом» груз лежит на каком-либо основании, канаты провисают, нагрузка на
- 17. Уравнение движения имеет вид:
- 18. Решение этого уравнения где уСТ – прогиб конструкции от статической нагрузки; V - установившаяся скорость подъема
- 20. Скачать презентацию












 Электромагниты. 8 класс
Электромагниты. 8 класс Презентация на тему Сила трения
Презентация на тему Сила трения  Введение в предмет Микросхемотехника
Введение в предмет Микросхемотехника Резисторы и Реостаты. Занятие 7
Резисторы и Реостаты. Занятие 7 Резонансные методы передачи электрической энергии
Резонансные методы передачи электрической энергии Закон Максвелла. Электромагнитное поле
Закон Максвелла. Электромагнитное поле Электризация тел
Электризация тел Как устроен строительный экскаватор и что такое гидравлический цилиндр?
Как устроен строительный экскаватор и что такое гидравлический цилиндр? Магнетизм. Структурно-логическая схема. Условные обозначения
Магнетизм. Структурно-логическая схема. Условные обозначения Работа по физике. Правду ли говорят
Работа по физике. Правду ли говорят Презентация на тему Влияние магнитных полей на живые организмы
Презентация на тему Влияние магнитных полей на живые организмы  Рулевое устройство
Рулевое устройство Фотометрия и светотехника. ВИК - простая форма обучения
Фотометрия и светотехника. ВИК - простая форма обучения Скин-фактор. Различные режимы притока. Уравнение притока
Скин-фактор. Различные режимы притока. Уравнение притока Дозиметрия. Период полураспада. Закон радиоактивного распада
Дозиметрия. Период полураспада. Закон радиоактивного распада Покоривший волны
Покоривший волны Расчет характеристик световой волны. Практическая работа №21
Расчет характеристик световой волны. Практическая работа №21 Поколения ядерных реакторов. Лекция 6
Поколения ядерных реакторов. Лекция 6 Мир вокруг нас
Мир вокруг нас Инструменты и приборы
Инструменты и приборы Механическая работа. Единицы работы
Механическая работа. Единицы работы Спектроскопические методы анализа
Спектроскопические методы анализа Решения задач по теме Плавление и отвердевание кристаллических тел
Решения задач по теме Плавление и отвердевание кристаллических тел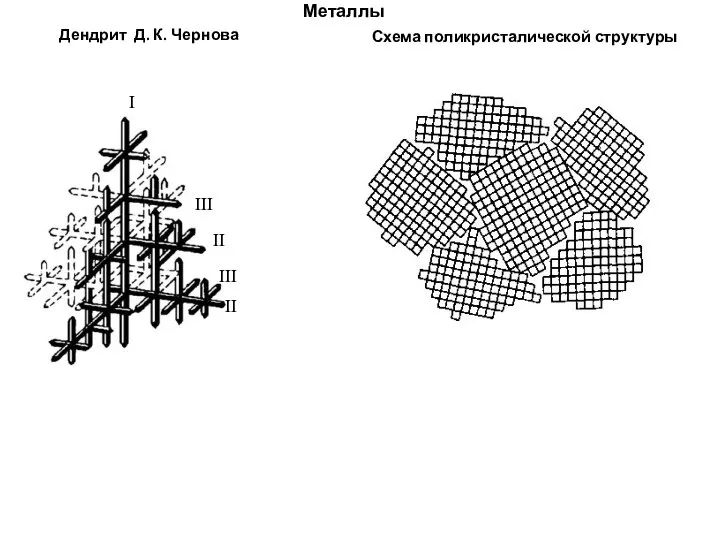 Металлы. Дендрит Д.К. Чернова
Металлы. Дендрит Д.К. Чернова Количество теплоты
Количество теплоты Методы инструментального выявления недостоверного учета электрической энергии
Методы инструментального выявления недостоверного учета электрической энергии Презентация на тему Оптические приборы
Презентация на тему Оптические приборы  Активация в ядерной физике. (Тема 2.8)
Активация в ядерной физике. (Тема 2.8)