Содержание
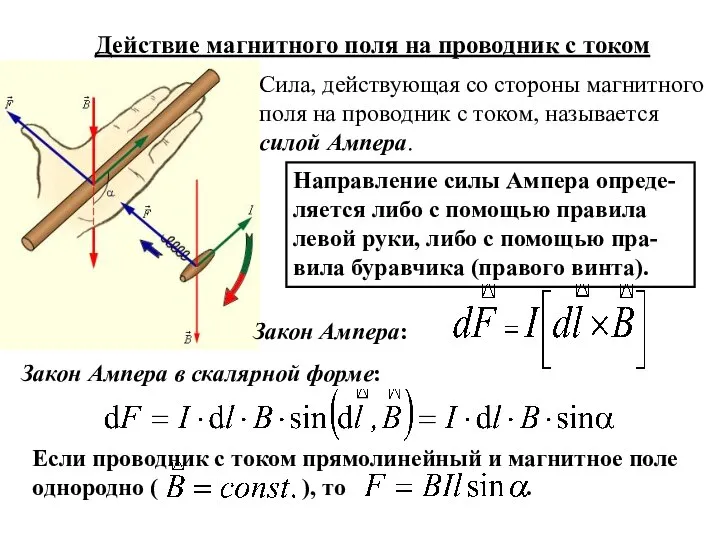
- 2. Действие магнитного поля на проводник с током Сила, действующая со стороны магнитного поля на проводник с
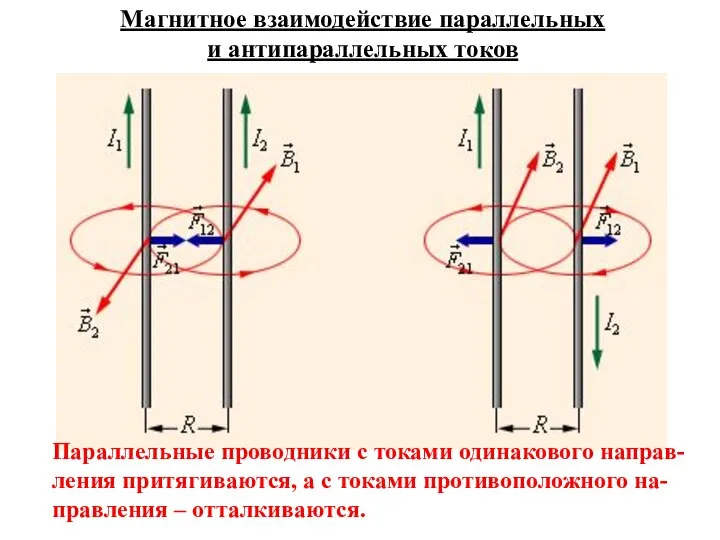
- 3. Взаимодействие параллельных проводников с током По закону Био-Савара-Лапласа: По закону Ампера: При и : Параллельные проводники
- 4. Параллельные проводники с токами одинакового направ-ления притягиваются, а с токами противоположного на-правления – отталкиваются. Магнитное взаимодействие
- 5. Действие магнитного поля на движущийся заряд Сила, действующая со стороны магнитного поля на движущийся заряд, называется
- 6. (α = 0 или π; FЛ = 0). Движение прямолинейное и равномерное. 1. Частица движется вдоль
- 7. Если на движущуюся заряженную частицу одновременно действуют электрическое поле напряженностью и маг- нитное поле с индукцией
- 8. Эффект Холла (обнаружен в 1879 г.) Эффект Холла – это возникновение попе- речной разности по- тенциалов
- 9. Постоянная Холла Эдвин Герберт Холл (1855 – 1938) где – постоянная Холла. Измерив постоянную Холла, можно
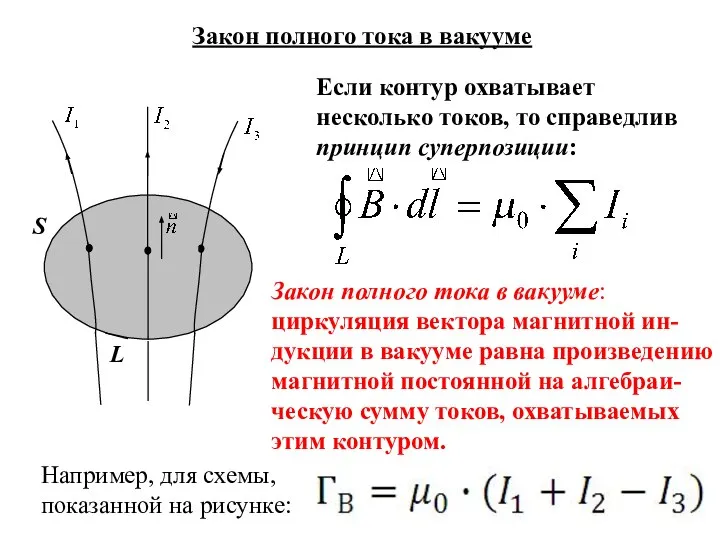
- 10. L – циркуляция вектора магнитной индукции. Циркуляция вектора магнитной индукции Если для электростатического поля всегда: то
- 11. Пример: вычислим циркуляцию вектора для прямо-линейного проводника с током в вакууме вдоль контура, совпадающего с одной
- 12. Если контур охватывает несколько токов, то справедлив принцип суперпозиции: Закон полного тока в вакууме Закон полного
- 13. Магнитный поток Магнитным потоком через площадку dS называется скалярная физическая величина – магнитный поток через Для
- 15. Скачать презентацию









 Презентация на тему Что изучает физика (7 класс)
Презентация на тему Что изучает физика (7 класс)  Подготовка машины к работе
Подготовка машины к работе Презентация на тему Идеальный газ в МКТ
Презентация на тему Идеальный газ в МКТ  Механика. Закон Архимеда
Механика. Закон Архимеда Презентация на тему Способы теплопередачи
Презентация на тему Способы теплопередачи  Презентация на тему Понятие силы трения
Презентация на тему Понятие силы трения  Однородное и неоднородное магнитное поле. Направление тока и направление линий его магнитного поля
Однородное и неоднородное магнитное поле. Направление тока и направление линий его магнитного поля Невагомiсть
Невагомiсть Нанотехнологии и их применение
Нанотехнологии и их применение Ядерный реактор
Ядерный реактор Теория горения и взрывов. Кинетическая реакция горения. Лекция 3
Теория горения и взрывов. Кинетическая реакция горения. Лекция 3 Интегрирование дифференциальных уравнений движения мотоцикла
Интегрирование дифференциальных уравнений движения мотоцикла Инфракрасное и ультрафиолетовое излучение
Инфракрасное и ультрафиолетовое излучение Роль машиностроения и этапы его развития. Тема 1
Роль машиностроения и этапы его развития. Тема 1 Первичные и вторичные параметры длинной линии. Лекция Д1
Первичные и вторичные параметры длинной линии. Лекция Д1 Методы регистрации элементарных частиц
Методы регистрации элементарных частиц Электроосветительные приборы
Электроосветительные приборы Lektsia_1 (1)
Lektsia_1 (1) Применение фотоэффекта
Применение фотоэффекта Лекция 4
Лекция 4 Технология критического мышления на уроках физики
Технология критического мышления на уроках физики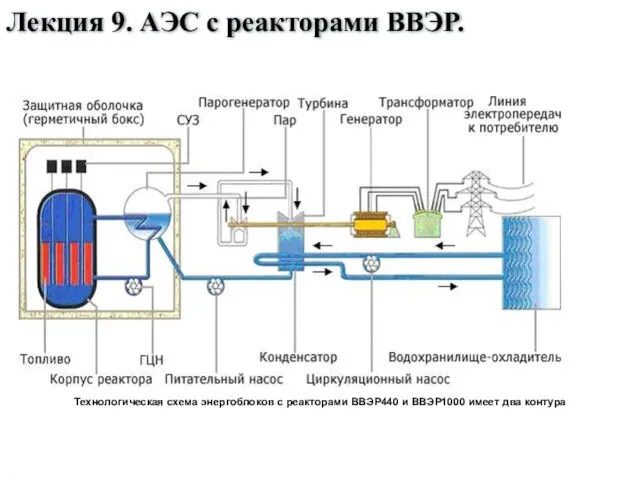 АЭС с реакторами ВВЭР. Лекция 9
АЭС с реакторами ВВЭР. Лекция 9 Течь жидкости ГУР
Течь жидкости ГУР На чем мы плаваем?
На чем мы плаваем? Проводники и диэлектрики
Проводники и диэлектрики Введение. Принципы радио- и телевещания. Особенности антенно-фидерных устройств и РРВ. Лекция 1,2
Введение. Принципы радио- и телевещания. Особенности антенно-фидерных устройств и РРВ. Лекция 1,2 Методическая разработка по применению первого закона термодинамики к решению графических задач
Методическая разработка по применению первого закона термодинамики к решению графических задач Прямоугольная яма
Прямоугольная яма