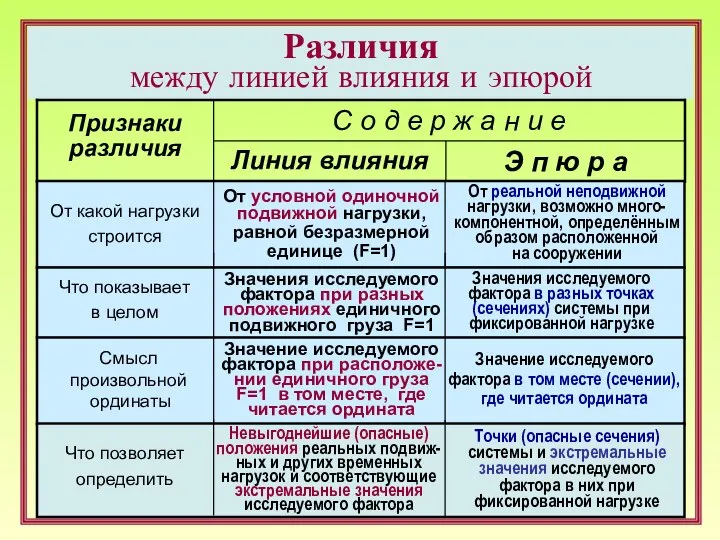
безразмерной
единице (F=1)
От реальной неподвижной нагрузки, возможно много-компонентной, определённым образом расположенной
на сооружении
Что показывает
в целом
Значения исследуемого фактора при разных положениях единичного подвижного груза F=1
Значения исследуемого фактора в разных точках (сечениях) системы при фиксированной нагрузке
Смысл
произвольной
ординаты
Значение исследуемого фактора при расположе-нии единичного груза F=1 в том месте, где читается ордината
Что позволяет
определить
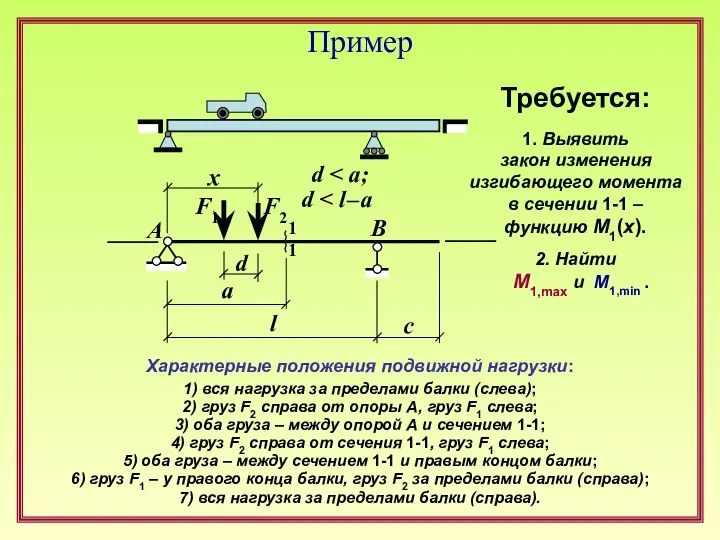
Невыгоднейшие (опасные) положения реальных подвиж-ных и других временных нагрузок и соответствующие экстремальные значения
исследуемого фактора
Точки (опасные сечения) системы и экстремальные значения исследуемого фактора в них при фиксированной нагрузке
Значение исследуемого фактора в том месте (сечении), где читается ордината




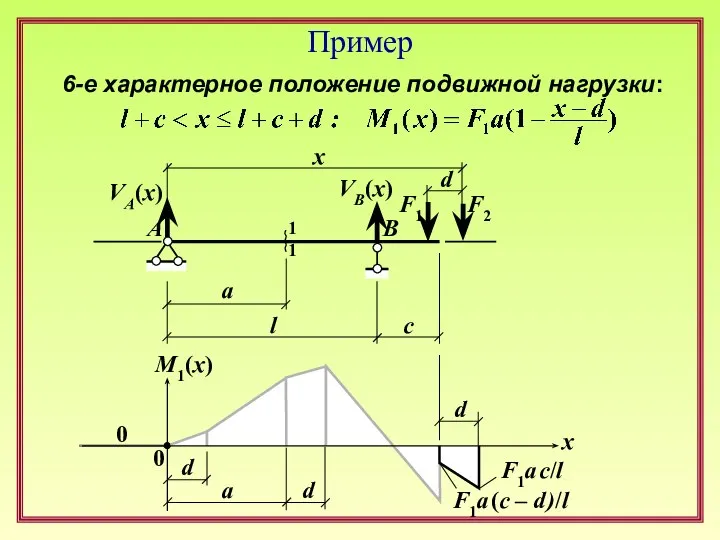
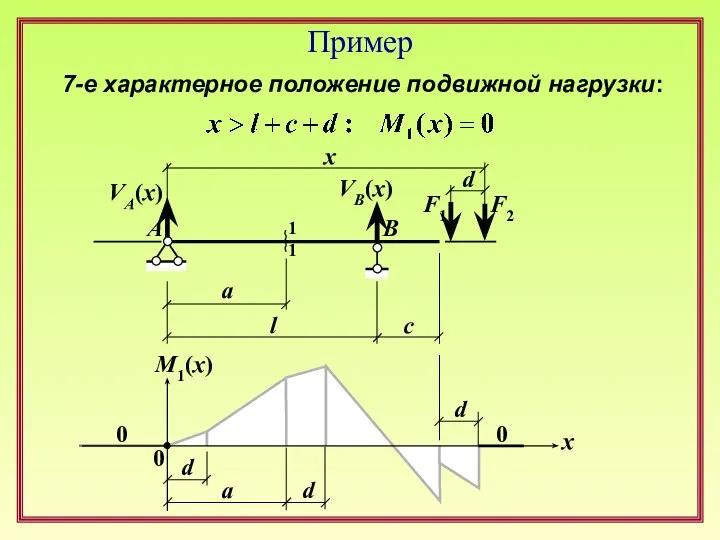
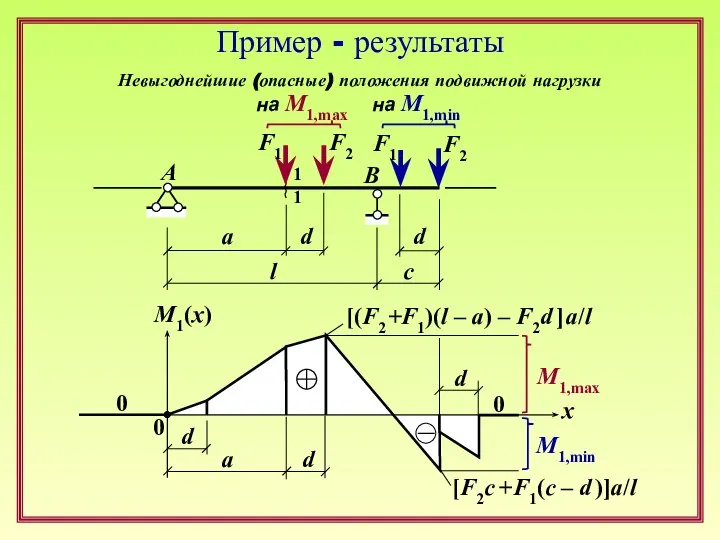
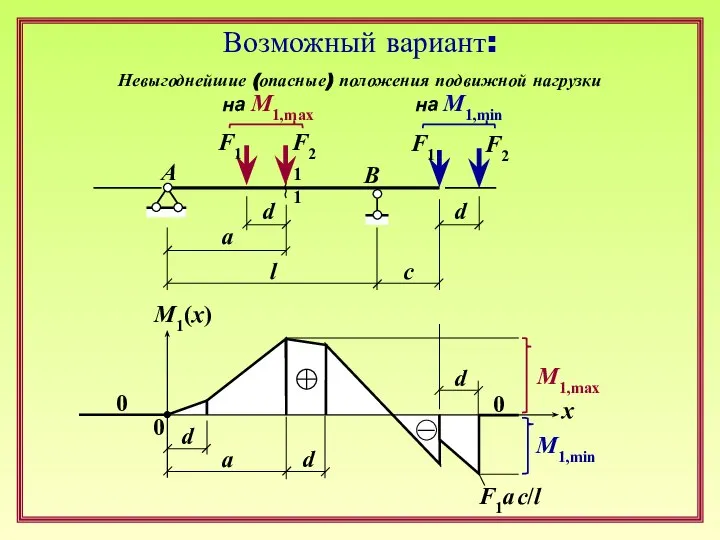

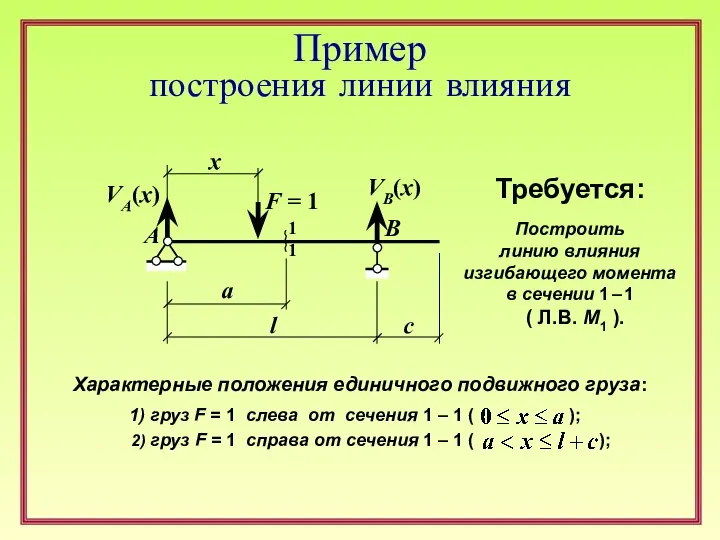
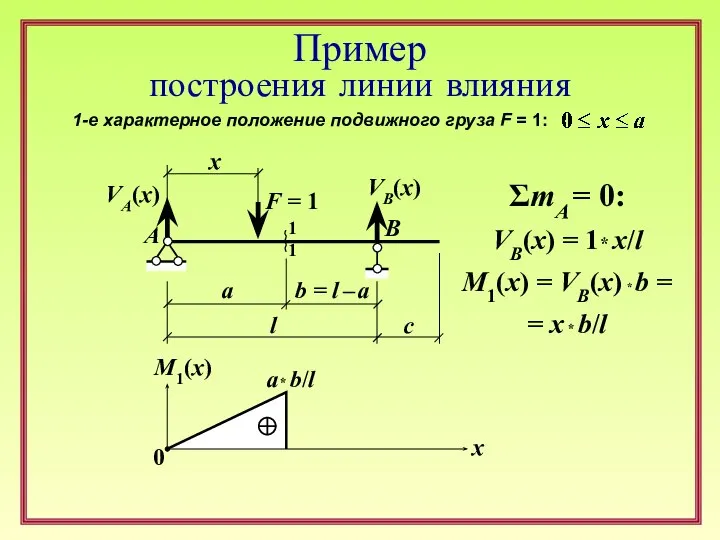
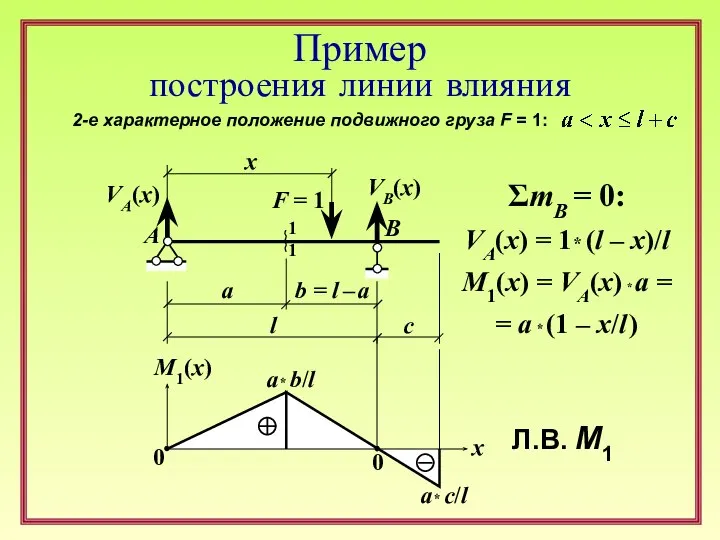
 Основы физической органической химии. Сигма-ро анализ
Основы физической органической химии. Сигма-ро анализ Геометрическая оптика. (Лекция 6)
Геометрическая оптика. (Лекция 6) Презентация на тему Движение тела, брошенного вертикально вверх
Презентация на тему Движение тела, брошенного вертикально вверх  Цепные передачи (ЦП)
Цепные передачи (ЦП) Гравитационные волны
Гравитационные волны Энергия связи
Энергия связи Винт Архимеда
Винт Архимеда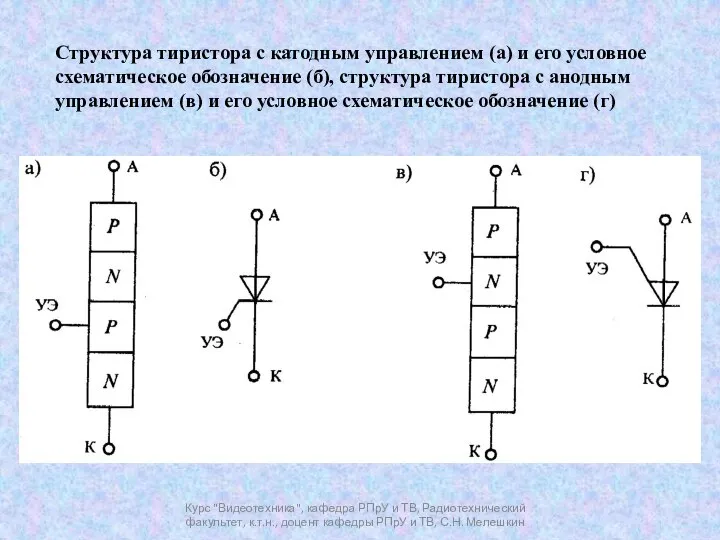 Тиристор
Тиристор Ускорение свободного падения а земле и других небесных телах
Ускорение свободного падения а земле и других небесных телах Фундаментальные физические величины. Упражнения. Часть 2
Фундаментальные физические величины. Упражнения. Часть 2 Презентация (4)
Презентация (4) Учимся мыслить
Учимся мыслить Магнитное поле Земли
Магнитное поле Земли Плотность вещества
Плотность вещества ТО системы зажигания искрового двигателя
ТО системы зажигания искрового двигателя Өлшеудің белгісіздігі туралы түсінік
Өлшеудің белгісіздігі туралы түсінік Презентация на тему Закон преломления света (8 класс)
Презентация на тему Закон преломления света (8 класс)  Сила тяжести
Сила тяжести Новая прдукция
Новая прдукция Топ5 самых перспективных разработок атомной отрасли (Команда МОУ Лицей №1 10 класс)
Топ5 самых перспективных разработок атомной отрасли (Команда МОУ Лицей №1 10 класс) Назначение, устройство и работа сцепления автомобиля КамАЗ 5320 его привод и пневмогидроусилитель
Назначение, устройство и работа сцепления автомобиля КамАЗ 5320 его привод и пневмогидроусилитель Радиоактивные превращения, ядерные реакции, энергия связи. Решение задач
Радиоактивные превращения, ядерные реакции, энергия связи. Решение задач L- jetronic
L- jetronic Условия, при которых тело плавает и при которых тонет
Условия, при которых тело плавает и при которых тонет Излучение и поглощение электромагнитных волн в среде. (Лекция 2)
Излучение и поглощение электромагнитных волн в среде. (Лекция 2) Звездный час (викторина)
Звездный час (викторина) Роль физики в современном мире
Роль физики в современном мире Тепловое действие электрического тока. Закон Джоуля-Ленца
Тепловое действие электрического тока. Закон Джоуля-Ленца