Тепловое излучение. Лекция 30

Существуют два вида излучения.
Тепловое излучение – испускание электромагнитных волн за счёт
внутренней (тепловой)
энергии тел.
Люминесценция – излучения,
возбуждаемые за счёт любого вида энергии,
кроме тепловой.

Виды люминесценции
- хемилюминесценция (свечение окисляющегося на воздухе фосфора за счёт энергии, выделяемой при химическом превращении);
- электролюминесценция (свечение, возникающее в газах и твёрдых телах под воздействием электрического поля);
- фотолюминесценция (свечение, возбуждаемое поглощаемым телом электромагнитным излучением).

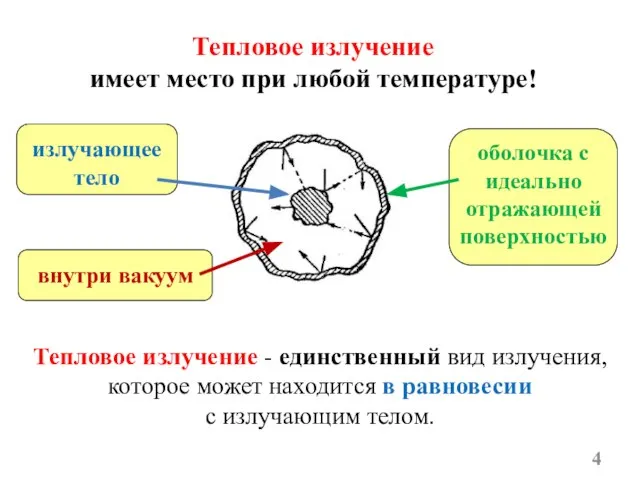
Тепловое излучение
имеет место при любой температуре!
излучающее
тело
оболочка с идеально отражающей поверхностью
внутри вакуум
Тепловое излучение - единственный вид излучения, которое может находится в равновесии
с излучающим телом.

Равновесность означает,
что тело в единицу времени
поглощает столько же энергии,
сколько и излучает.
Потому что любое нарушение равновесия
в системе тело-излучение
вызывает возникновение процессов, восстанавливающих равновесие.
Почему тепловое излучение равновесно?

Энергетическая светимость RT – энергия, излучаемая единицей поверхности излучающего тела за единицу времени по всем направлениям.
(Мощность излучения с единицы площади поверхности тела)
W – энергия, излучаемая всей поверхностью тела [Дж];
S – площадь поверхности [м2];
P – мощность излучения [Вт];
t – время излучения [с].
Энергетическая светимость RT – функция температуры T.

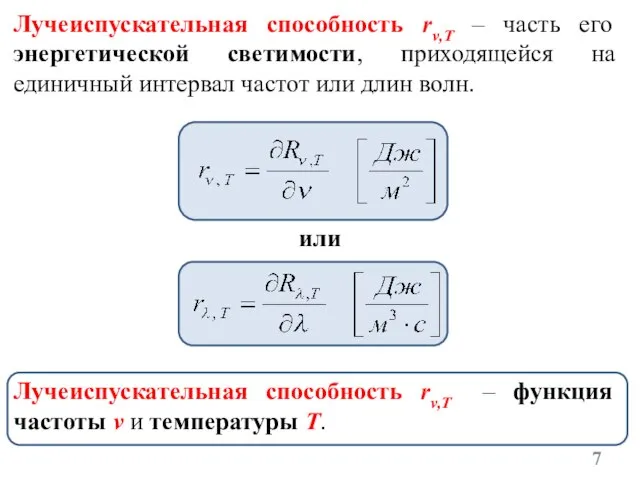
Лучеиспускательная способность rν,T – часть его энергетической светимости, приходящейся на единичный интервал частот или длин волн.
Лучеиспускательная способность rν,T – функция частоты ν и температуры T.

Интегральная форма записи энергетической светимости
Всегда

Как перейти от rν,T к rλ,T ?
Учтём, что , тогда
Знак «-» учитывает,
что с ростом одной величины (λ или ν),
другая величина убывает.

Перепишем выражения в виде
Воспользовавшись соотношением, получим

Спектральной поглощательная способность тела Aν,T
Спектральная поглощательная способность Aν,T –
функция частоты ν и температуры T.
Пусть на элементарную площадку поверхности тела падает лучистая энергия, переносимая электромагнитными волнами, частота которых заключена в интервале ν, ν+dν.
Часть данной энергии будет поглощена телом.

Очевидно, что всегда
Если
то такое тело называется абсолютно чёрным.
АЧТ - тело, способное поглощать при любой температуре всё падающее на него излучение любой частоты.

Наиболее близкими телами к АЧТ можно назвать:
чёрный бархат;
сажа (уголь) поглощает 96% света;
Vantablack - субстанция из углеродных нанотрубок. Поглощает 99,965% падающего на него излучения.
Пример: при наличии небольшого отверстия в замкнутой полости, свет, попавший туда, будет испытывать
многократные отражения и практически полностью поглотится.

Серое тело - тело, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела:

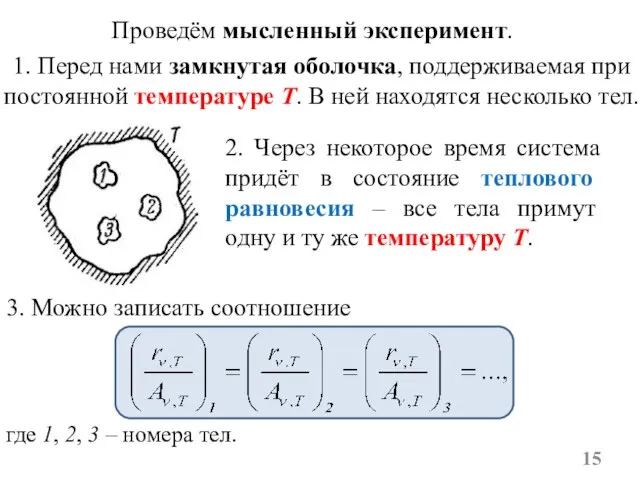
Проведём мысленный эксперимент.
2. Через некоторое время система придёт в состояние теплового равновесия – все тела примут одну и ту же температуру T.
3. Можно записать соотношение
где 1, 2, 3 – номера тел.
1. Перед нами замкнутая оболочка, поддерживаемая при постоянной температуре T. В ней находятся несколько тел.

Закон Кирхгофа
а. Отношение лучеиспускательной к поглощательной способности тела не зависит от природы тела и является универсальной для всех тел функцией частоты (длины волны) и температуры:
Кирхгоф
Густав Роберт
(1824-1887)

Определим вид универсальной функции Кирхгофа
Применим закон Кирхгофа к АЧТ
Для АЧТ
б. Для всех тел, отношение лучеиспускательной способности к спектральной поглощательной способности равно лучеиспускательной способности абсолютно черного тела при той же температуре.
Таким образом, универсальная функция Кирхгофа есть лучеиспускательная способность АЧТ.

Величины rν,T и Aν,T могут меняться
очень сильно при переходе
от одного тела к другому.
Но отношение этих величин
одинаково для всех тел!
Тело, сильнее поглощающее какие-либо лучи, будут эти лучи сильнее и испускать.

Энергетическая светимость серого тела

Энергетическая светимость чёрного тела пропорциональна четвёртой степени его термодинамической температуре.
Закон Стефана-Больцмана – постоянная Стефана-Больцмана;
T – термодинамическая температура [К].
Стефан
Йозеф
(1835-1893)
Больцман
Людвиг
(1844-1906)

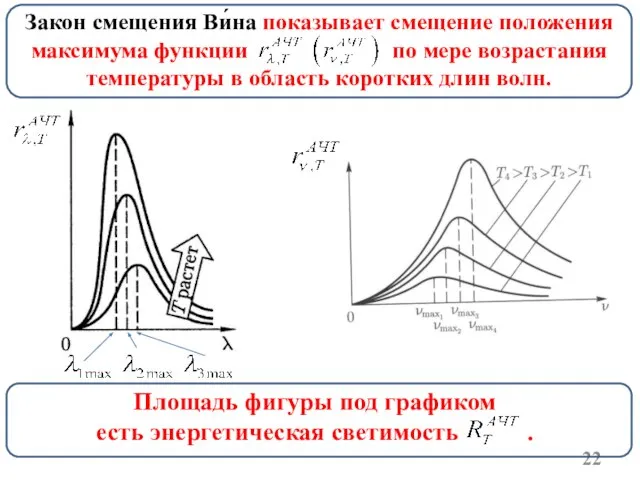
Закон смещения Ви́на
λmax – длина волны, соответствующая максимальному значению лучеиспускательной способности АЧТ [м];
b=2,9·10-3 – постоянная Ви́на [м·К];
T – температура [К].
Длина волны, соответствующая максимальному значению лучеиспускательной способности АЧТ, обратно пропорциональна его абсолютной температуре.
Вин
Вильгельм
(1864 - 1928)
Спектр АЧТ – распределение лучеиспускательной способности АЧТ по длинам волн.

Площадь фигуры под графиком
есть энергетическая светимость .
Закон смещения Ви́на показывает смещение положения максимума функции по мере возрастания температуры в область коротких длин волн.

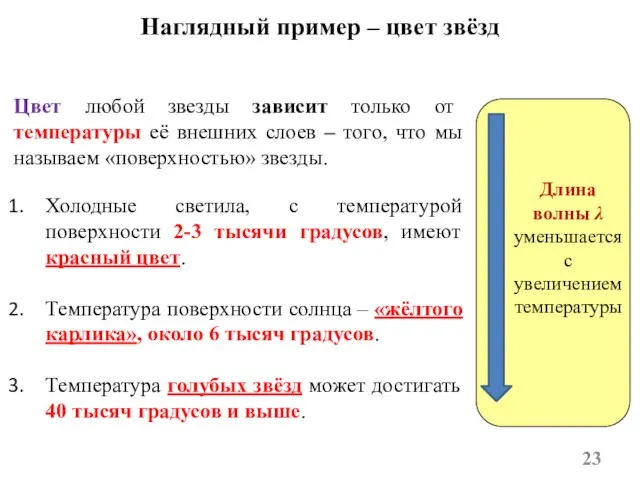
Наглядный пример – цвет звёзд
Цвет любой звезды зависит только от температуры её внешних слоев – того, что мы называем «поверхностью» звезды.
Холодные светила, с температурой поверхности 2-3 тысячи градусов, имеют красный цвет.
Температура поверхности солнца – «жёлтого карлика», около 6 тысяч градусов.
Температура голубых звёзд может достигать 40 тысяч градусов и выше.
Длина волны λ уменьшается с увеличением температуры

Созвездие Ориона
Звезда Бетельгейзе красного цвета
Звезда Ригель
голубовато-белого цвета

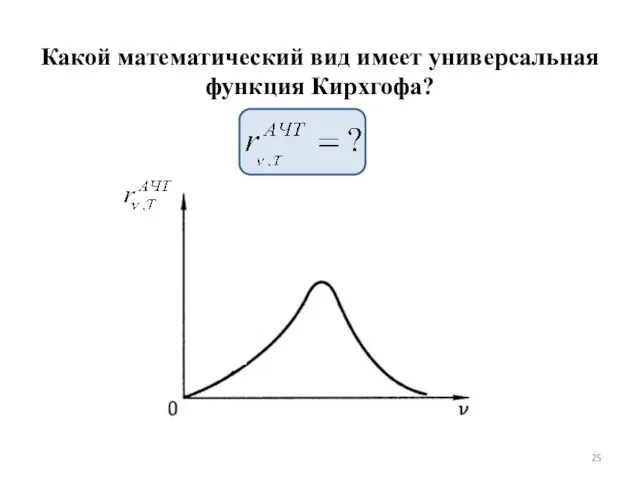
Какой математический вид имеет универсальная функция Кирхгофа?

Формула Рэлея-Джинса
k=1,38·10-23 – постоянная Больцмана [Дж/К];
T – абсолютная температура [К].
Стретт, Джон Уильям
(лорд Рэлей)
(1842 - 1919)
Джинс
Джеймс Хопвуд
(1877 - 1946)
Рэлей и Джинс получили зависимость от частоты света, используя методы классической статистической физики.
Они предположили, опираясь на теорему о равнораспределении энергии по степеням свободы, что на каждое электромагнитное колебание приходится в среднем энергия равная kT.

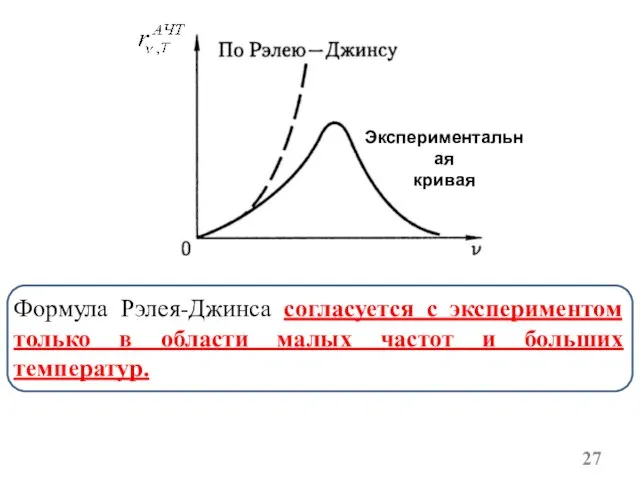
Формула Рэлея-Джинса согласуется с экспериментом только в области малых частот и больших температур.

Мы видим, что неограниченно растёт, достигая чрезвычайно больших значений в ультрафиолете (7,5·1014-3·1017 Гц).
Этот результат получил название «ультрафиолетовая катастрофа».

Эта неудача свидетельствовала о
недостатках
в классической теории физики.

РЕВОЛЮЦИЯ В ФИЗИКЕ. 1900 ГОД.
Квантовая гипотеза Планка
h=6,625·10-34 – постоянная Планка [Дж·с];
с=3·108 – скорость света в вакууме [м/с];
λ – длина волны света [м].
ν – частота волны света [Гц].
Атомные осцилляторы излучают энергию не непрерывно, а дискретно, определёнными порциями – квантами.
- энергия кванта.

Поскольку энергия излучается порциями, то энергия осциллятора может принимать лишь определённые дискретные значения, кратные целому числу квантов:
Формула Планка
Формула Планка, хорошо согласуется с экспериментальными данными по распределению энергии в спектре излучения АЧТ, во всём интервале частот и температур.
а.

Особый случай Энергия кванта очень мала по сравнению с энергией теплового движения kT.
Формула Планка переходит в формулу Рэлея-Джинса.
б.

Доказательство.
Подставим (*) в формулу Планка
формула Рэлея-Джинса

Получим из формулы Планка формулу Стефана-Больцмана.
Введём безразмерную переменную

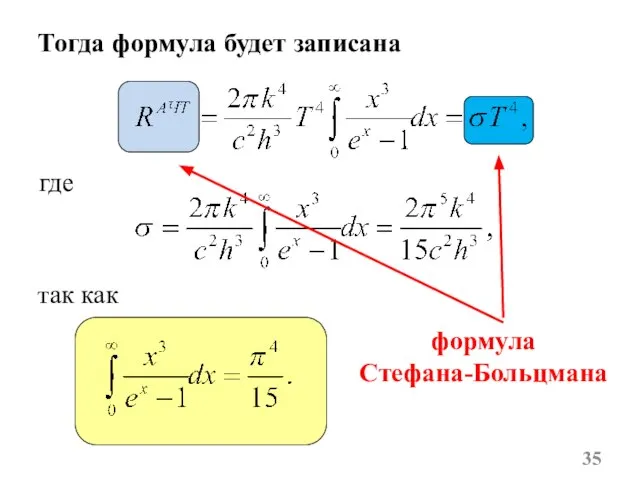
Тогда формула будет записана
где
так как
формула
Стефана-Больцмана

Получим из формулы Планка закон Ви́на с помощью (7) и (17)
откуда

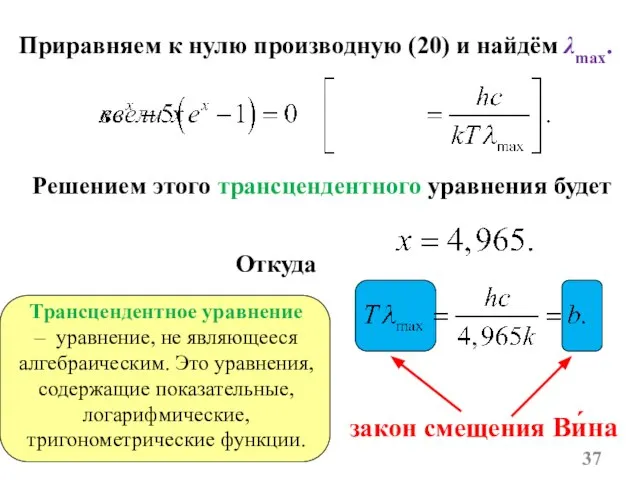
Приравняем к нулю производную (20) и найдём λmax.
Решением этого трансцендентного уравнения будет
Откуда
закон смещения Ви́на
Трансцендентное уравнение – уравнение, не являющееся алгебраическим. Это уравнения, содержащие показательные, логарифмические, тригонометрические функции.