способы решения
Система уравнений Максвелла для электромагнитного поля: смысл, способы решения
Полезно знать Подготовка к экзамену Физика для "чайников"
Иван27 Июнь 201717 264
Нет времени писать работу?
Доверь это кандидату наук!
Узнай стоимость
Содержание
Содержание
Первое уравнение Максвелла
Третье уравнение Максвелла
Второе уравнение Максвелла
Четвертое уравнение Максвелла
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
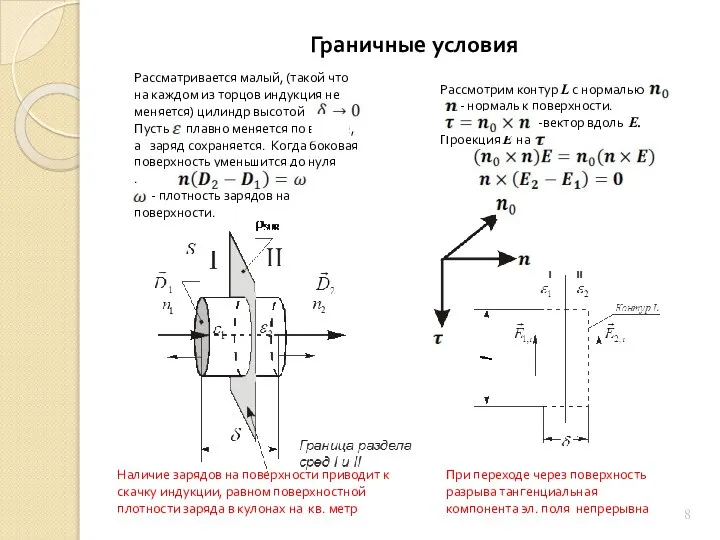
Стационарное электрическое поле
Первое уравнение: электрический заряд порождает электрическое поле
Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле
Третье уравнение: магнитных зарядов не существует
Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле
Уравнения Максвелла
Исключив зависимость от времени, получаем:
Из второго следует, что Е можно представить в виде
- скалярный потенциал
Минус выбран для того, чтобы выполнить общепринятое условие:
«вектор Е направлен от положительного заряда к отрицательному»



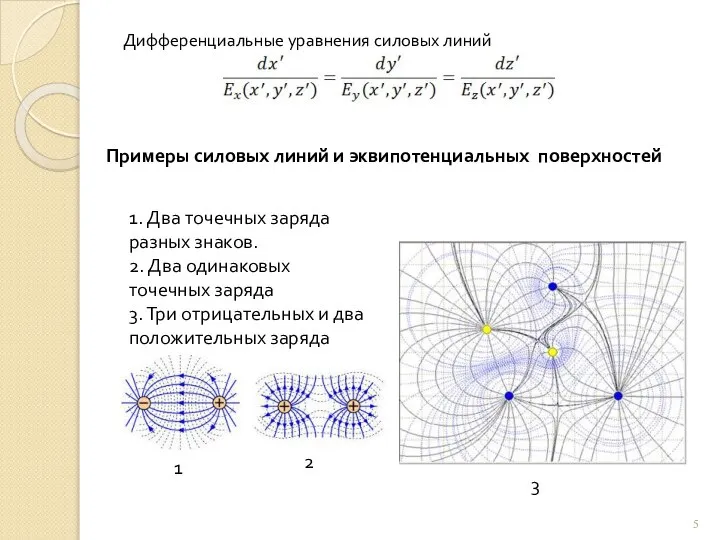
















 Главные центральные оси сечения
Главные центральные оси сечения Колебания и волны (ОГЭ). Решение задач 9 класс
Колебания и волны (ОГЭ). Решение задач 9 класс Конденсатор
Конденсатор Силы осмоса. Как варить вкусную картошку
Силы осмоса. Как варить вкусную картошку Режим натуральной мощности
Режим натуральной мощности Закон сохранения энергии
Закон сохранения энергии Физические свойства металлов
Физические свойства металлов Линзы. Основные элементы
Линзы. Основные элементы Статика. Физика
Статика. Физика Волновая оптика
Волновая оптика Законы сохранения
Законы сохранения Алессандро Вольта - Электрическая батарея
Алессандро Вольта - Электрическая батарея Голография. Её физические принципы
Голография. Её физические принципы Управление параметрами излучения мультиферроиковой структуры электрическим полем
Управление параметрами излучения мультиферроиковой структуры электрическим полем Автономные инверторы
Автономные инверторы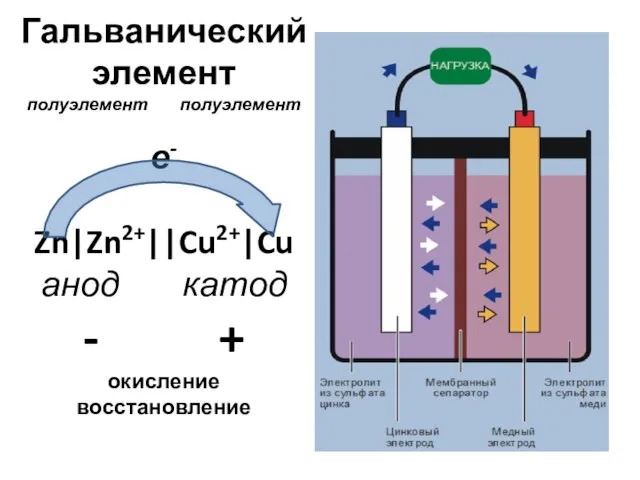 Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление
Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление Квалификационная работа Проект специализированной СТОА Honda на 5 рабочих постов с технологией замены топливного фильтра
Квалификационная работа Проект специализированной СТОА Honda на 5 рабочих постов с технологией замены топливного фильтра Испарение. Насыщенный и ненасыщенный пар. Поглощение энергии при испарении жидкости и выделение ее при конденсации пара
Испарение. Насыщенный и ненасыщенный пар. Поглощение энергии при испарении жидкости и выделение ее при конденсации пара Физика в картинках
Физика в картинках Основные приемы резания тонколистого металла и проволоки
Основные приемы резания тонколистого металла и проволоки Разветвленные цепи переменного тока
Разветвленные цепи переменного тока Презентация на тему Температура
Презентация на тему Температура  Двигатели технический систем
Двигатели технический систем Теплотехника. Основные определения и понятия. Параметры состояния. Уравнения состояния
Теплотехника. Основные определения и понятия. Параметры состояния. Уравнения состояния Презентация на тему Электромагнитная индукция
Презентация на тему Электромагнитная индукция  Явление самоиндукции
Явление самоиндукции Кинематика материальной точки. Тема №1
Кинематика материальной точки. Тема №1 Параметры эвольвентного зубчатого зацепления
Параметры эвольвентного зубчатого зацепления