Содержание
- 2. Неинерциальные СО – системы отсчёта, движущиеся относительно инерциальных систем отсчета с ускорением. Геоцентрическая система отсчета (жёстко
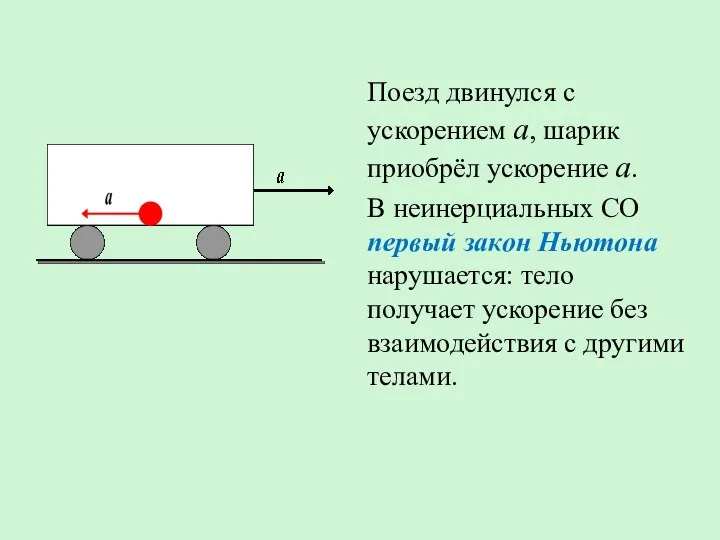
- 3. Поезд двинулся с ускорением а, шарик приобрёл ускорение а. В неинерциальных СО первый закон Ньютона нарушается:
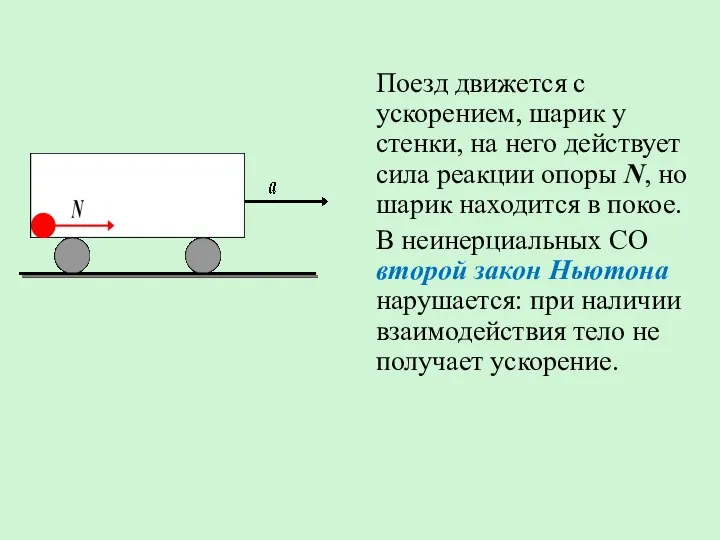
- 4. Поезд движется с ускорением, шарик у стенки, на него действует сила реакции опоры N, но шарик
- 5. В момент t = 0 системы К и К′ совпадают. Система К′ начинает двигаться относительно К
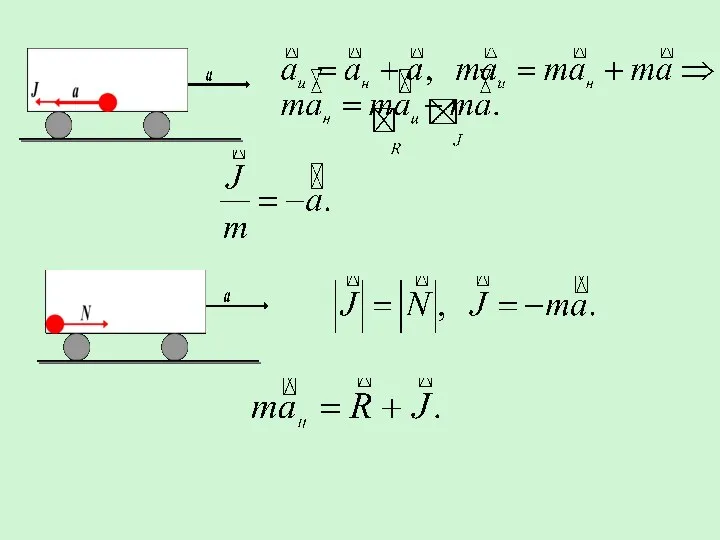
- 6. Продифференцируем уравнение (1) по времени: ан – ускорение материальной точки относительно НСО, аи – ускорение материальной
- 7. – векторная сумма сил взаимодействия, – сила инерции. Произведение массы тела на его ускорение относительно НСО
- 8. Сила инерции – фиктивная сила в том смысле, что она не обусловлена взаимодействием с другими телами,
- 10. Центробежная сила инерции во вращающихся СО зависит от местоположения тела в СО. n – единичный орт.
- 11. Свойства центробежной силы: 1) величина центробежной силы инерции (Fц.б) зависит от положения тела во вращающейся СО,
- 12. т.е. не зависит от формы пути.
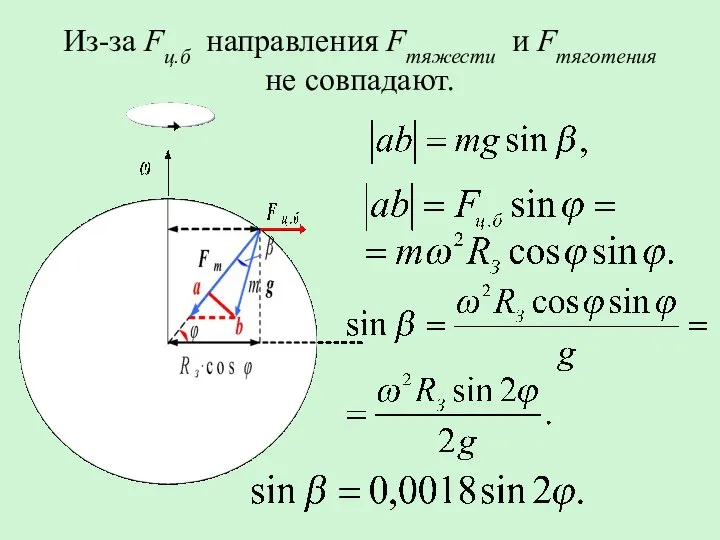
- 13. Из-за Fц.б направления Fтяжести и Fтяготения не совпадают.
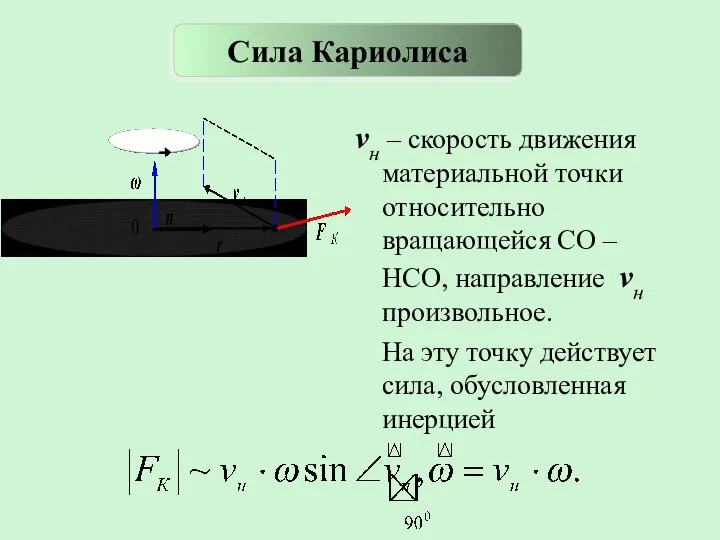
- 14. vн – скорость движения материальной точки относительно вращающейся СО –НСО, направление vн произвольное. На эту точку
- 15. Скорость точки относительно ИСО: Пусть
- 16. В общем случае Если материальная точка движется во вращающейся СО со скоростью vн, то на материальную
- 17. Свойства силы Кариолиса: 1) величина FК не зависит от положения материальной точки во вращающейся СО, 2)
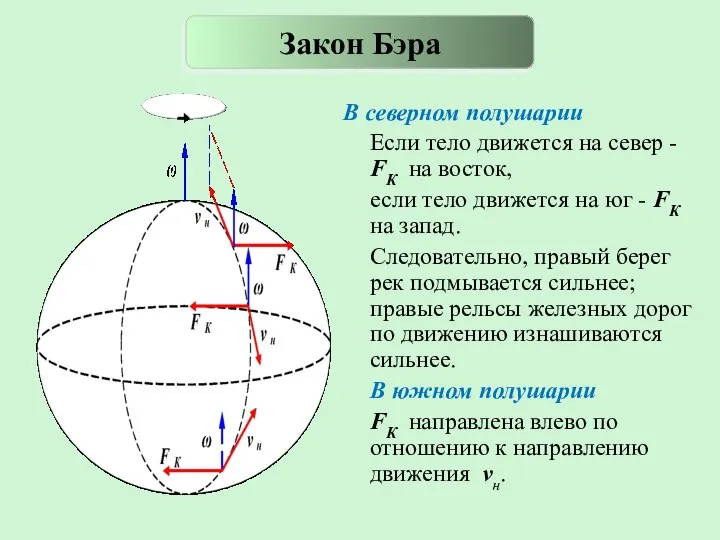
- 18. В северном полушарии Если тело движется на север - FК на восток, если тело движется на
- 19. Фундаментальные взаимодействия: электронное, гравитационное, сильное, слабое. Гравитационное взаимодействие универсальное, т.е. возникает между любыми двумя материальными точками.
- 20. Первая формулировка дана Ньютоном в 1687 г. в труде «Математические начала натуральной философии». Гравитационная масса –
- 21. Это векторная величина, численно равная силе, действующей на единицу массы, помещенную в данную точку поля и
- 22. Если гравитационное поле создано системой материальных точек (гравитационных масс), то результирующая напряженность поля равна векторной сумме
- 23. Гравитационные силы консервативные. Работа в гравитационном поле
- 24. Потенциальная энергия в поле тяготения. Сравнивая уравнении (1) и (2), запишем
- 25. Потенциал поля тяготения в данной точке равен потенциальной энергии тела единичной массы, помещенного в данную точку
- 26. Эквипотенциальные поверхности Геометрическое место точек, потенциал которых одинаков, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Для
- 27. «Взвешивание» (определение массы) Солнца, Земли, планет М – масса Солнца, R – расстояние между Землёй и
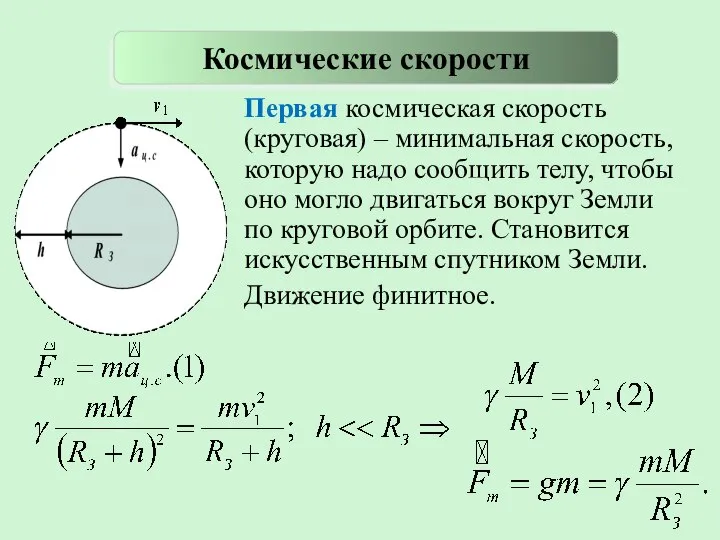
- 28. Первая космическая скорость (круговая) – минимальная скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг
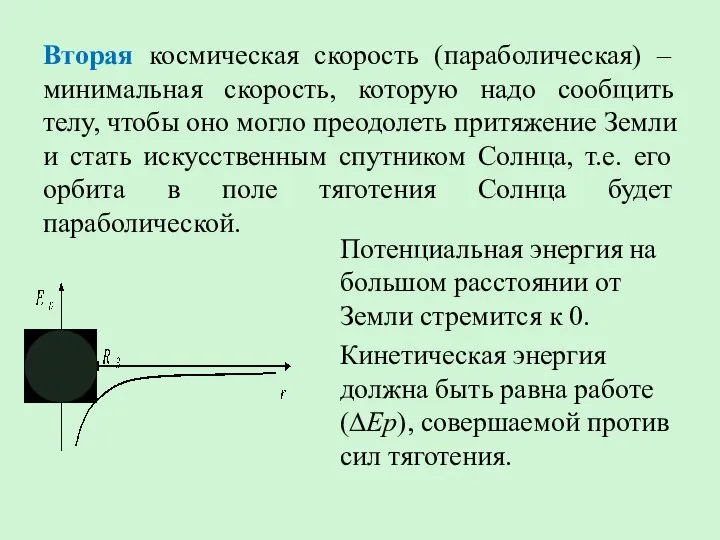
- 30. Вторая космическая скорость (параболическая) – минимальная скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение
- 32. Третья космическая скорость – скорость, которую надо сообщить телу, чтобы оно преодолело притяжение Солнца и покинуло
- 33. Описывают движение тел в центральном поле, каковым является поле тяготение. Кеплер (1571 – 1630 гг.) уточнил
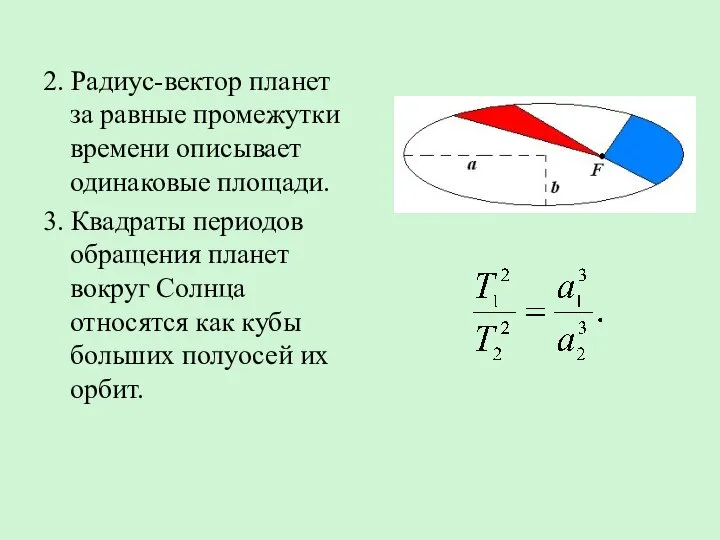
- 34. 2. Радиус-вектор планет за равные промежутки времени описывает одинаковые площади. 3. Квадраты периодов обращения планет вокруг
- 35. Для круговых орбит a = R. Законы Кеплера являются следствием законов Ньютона. Например, третий закон Кеплера.
- 36. Чёрные дыры – космические объекты, поглощающие все частицы, в том числе фотоны, проходящие через их поверхность.
- 38. Скачать презентацию




















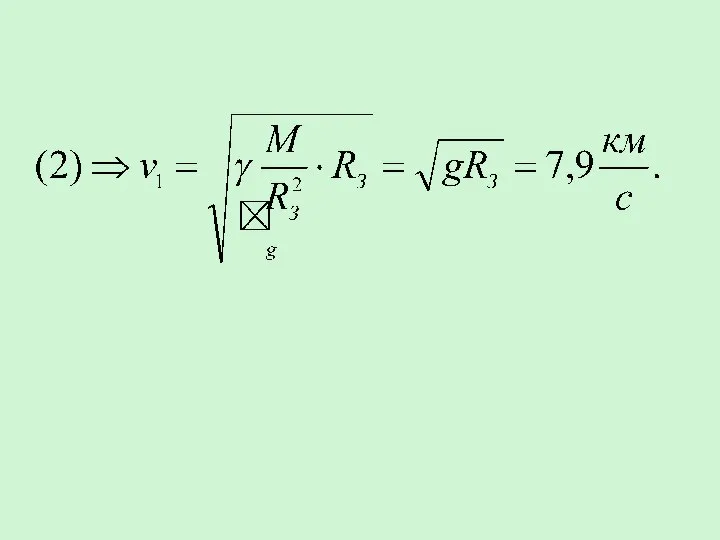
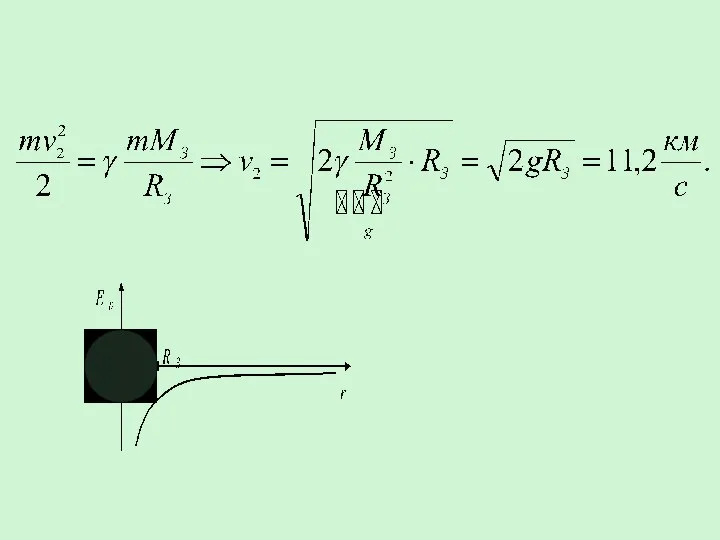




 Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 8
Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 8 Техническое обслуживание, диагностирование и ремонт жидкостной системы охлаждения автомобильного двигателя
Техническое обслуживание, диагностирование и ремонт жидкостной системы охлаждения автомобильного двигателя Светодиодное растениеводческое освещение
Светодиодное растениеводческое освещение Презентация на тему Открытие нейтрона. Строение атомного ядра
Презентация на тему Открытие нейтрона. Строение атомного ядра  Механика. Закон Архимеда
Механика. Закон Архимеда Теоретические основы электротехники. Теория электромагнитного поля. Лекция 4
Теоретические основы электротехники. Теория электромагнитного поля. Лекция 4 Грузовой автомобиль категории N2 с разработкой конструкции, технологии обслуживания и ремонта переднего моста
Грузовой автомобиль категории N2 с разработкой конструкции, технологии обслуживания и ремонта переднего моста Теория гироскопов
Теория гироскопов Назначение и устройство шатунов, шатунных подшипников и поршней дизелей. Порядок расположения кривошипов валов
Назначение и устройство шатунов, шатунных подшипников и поршней дизелей. Порядок расположения кривошипов валов Сила тока. Измерение силы тока
Сила тока. Измерение силы тока Работа газа и пара при расширении. Двигатели внутреннего сгорания
Работа газа и пара при расширении. Двигатели внутреннего сгорания Динамика жидкости и газа с учетом температуры
Динамика жидкости и газа с учетом температуры Устройство и история счетчиков электроэнергии
Устройство и история счетчиков электроэнергии Механические колебания. Звуковые волны. Акустика
Механические колебания. Звуковые волны. Акустика Механические колебания
Механические колебания Элективный курс Экспериментальная физика
Элективный курс Экспериментальная физика Источники радиоактивных загрязнений
Источники радиоактивных загрязнений Работы силы. Мощность. КПД
Работы силы. Мощность. КПД Закон Ома для участка цепи. Сопротивление
Закон Ома для участка цепи. Сопротивление Кіріспе. Термодинамикалық жүйе, процесс және тепе-теңдік
Кіріспе. Термодинамикалық жүйе, процесс және тепе-теңдік Контактные методы экологического мониторинга
Контактные методы экологического мониторинга Осветительные приборы наших предков
Осветительные приборы наших предков ЭДС индукции в движущихся проводниках. Решение задач
ЭДС индукции в движущихся проводниках. Решение задач Свободное падение
Свободное падение Строение атома
Строение атома Теплоносители и их свойства. Техническая термодинамика. (Тема 1)
Теплоносители и их свойства. Техническая термодинамика. (Тема 1) Электроосветительные установки
Электроосветительные установки High-speed Machining
High-speed Machining