Содержание
- 2. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Много ли
- 3. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Для описания
- 4. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Много ли
- 5. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Требуется стохастическое
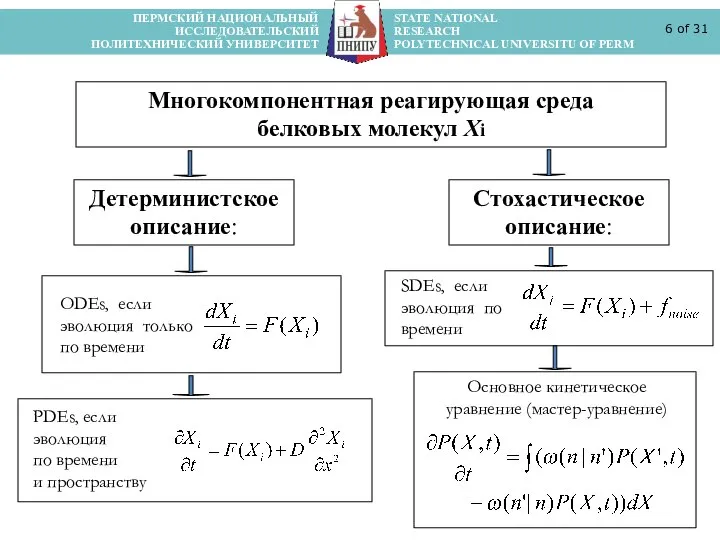
- 6. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Многокомпонентная реагирующая
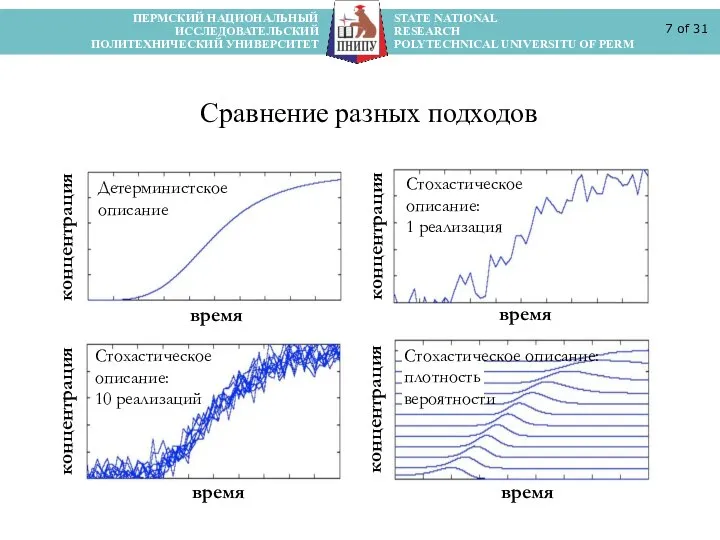
- 7. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Сравнение разных
- 8. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Полезная книга:
- 9. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Мастер-уравнение (основное
- 10. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Мастер-уравнение (основное
- 11. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Мастер-уравнение (основное
- 12. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Мастер-уравнение (основное
- 13. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Мастер-уравнение легко
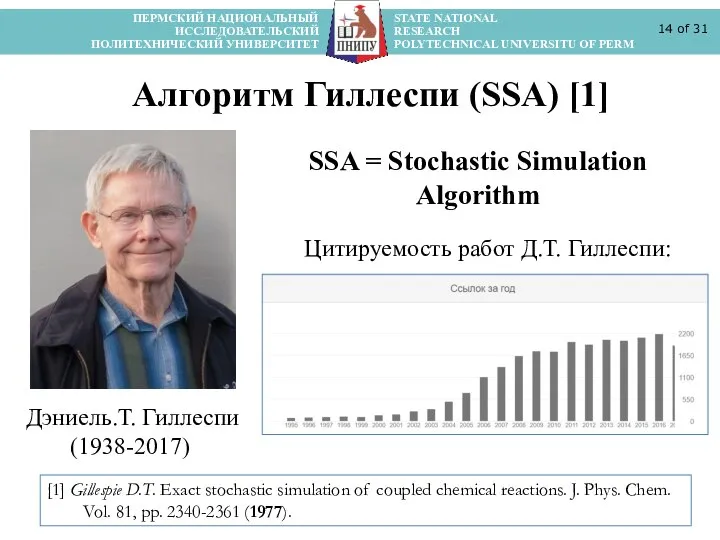
- 14. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Алгоритм Гиллеспи
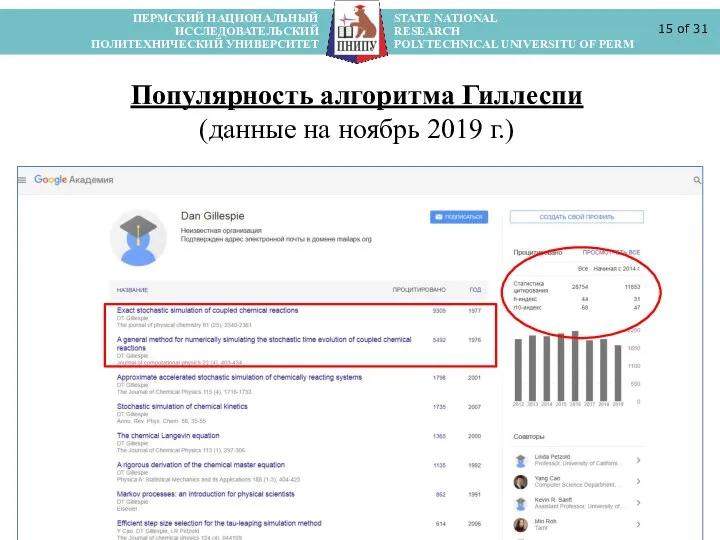
- 15. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Популярность алгоритма
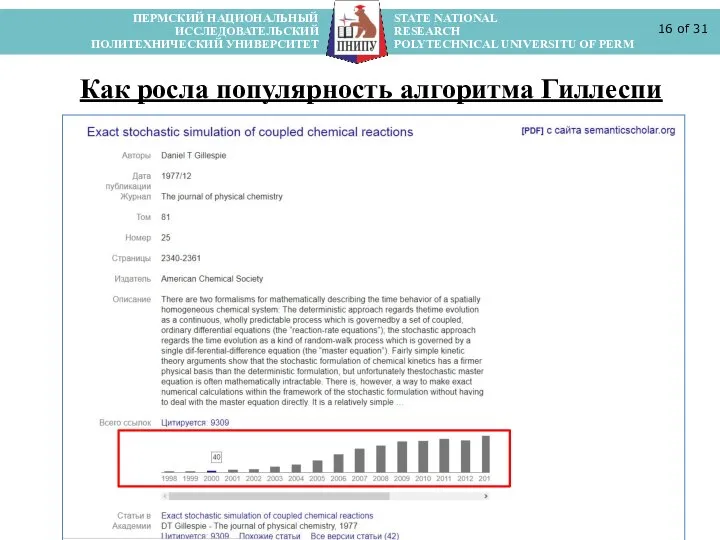
- 16. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Как росла
- 17. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Взрывной рост
- 18. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 шаги по
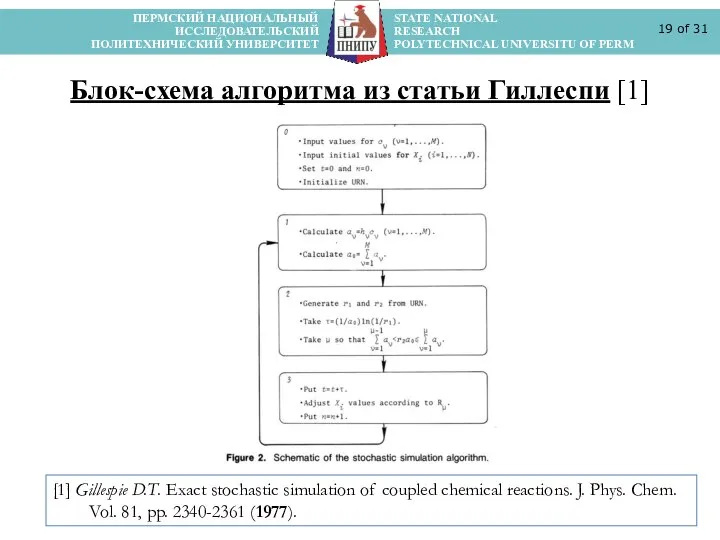
- 19. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 [1] Gillespie
- 20. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Алгоритм Гиллеспи
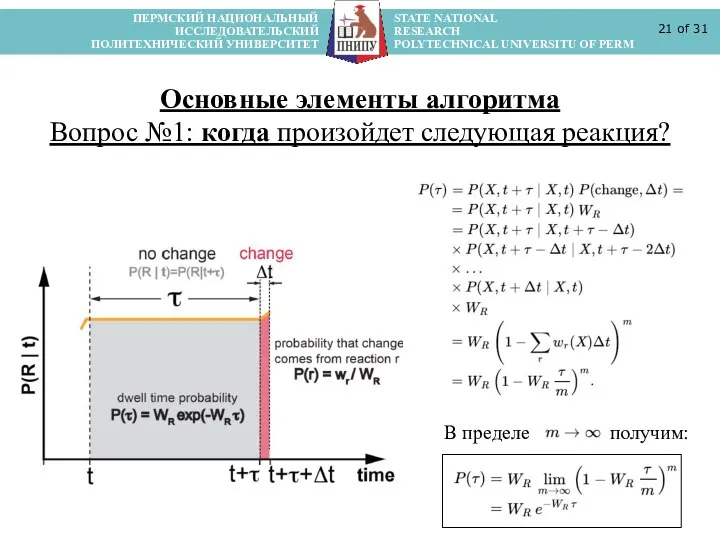
- 21. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Основные элементы
- 22. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Основные элементы
- 23. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Основные элементы
- 24. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Основные элементы
- 25. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 шаги по
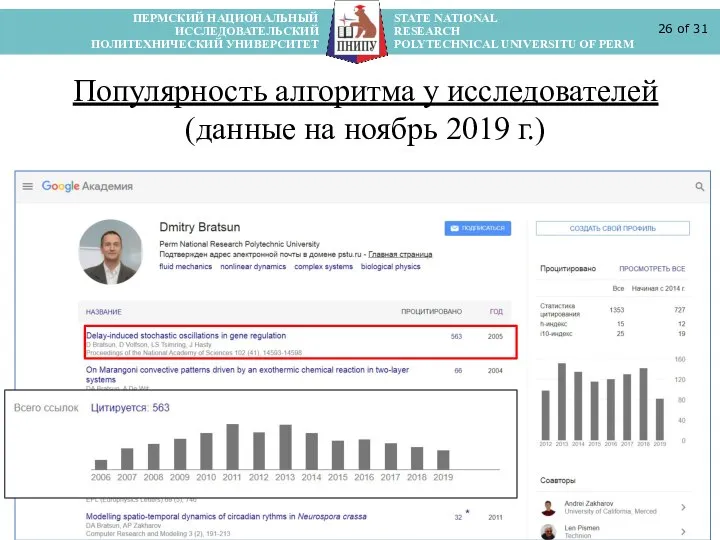
- 26. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Популярность алгоритма
- 27. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Стохастическое описание
- 28. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Точное решение
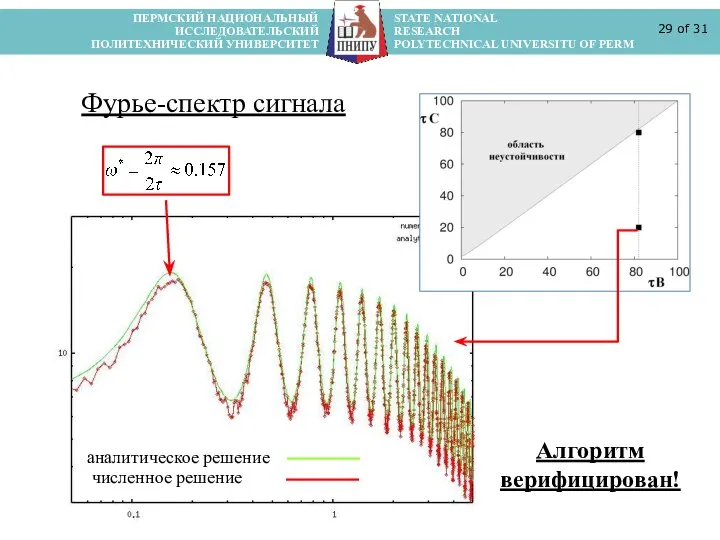
- 29. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 аналитическое решение
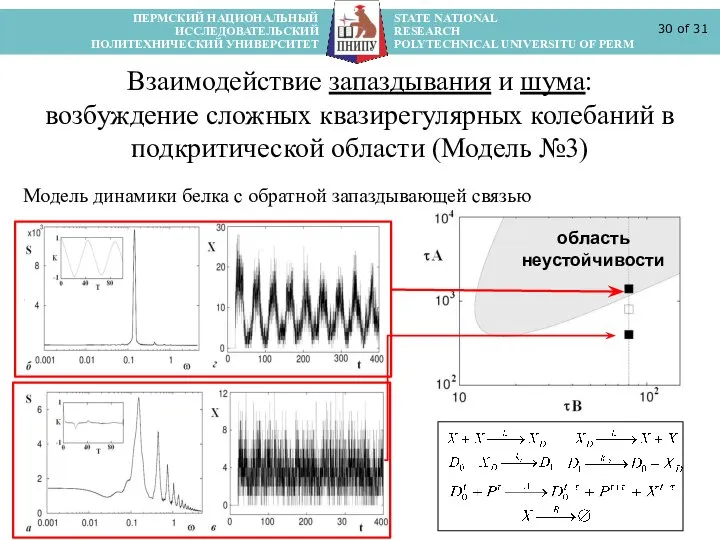
- 30. ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ STATE NATIONAL ИССЛЕДОВАТЕЛЬСКИЙ RESEARCH ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ POLYTECHNICAL UNIVERSITU OF PERM of 31 Взаимодействие запаздывания
- 32. Скачать презентацию



















 Подготовка машины к работе
Подготовка машины к работе Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1
Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1 Регулирование с воздействием по возмущению
Регулирование с воздействием по возмущению Типы астрономических объектов: галактики, звезды, планеты, астероиды, кометы, диффузное вещество
Типы астрономических объектов: галактики, звезды, планеты, астероиды, кометы, диффузное вещество Физика для одноклассников
Физика для одноклассников Обобщающий урок по механике (10 класс)
Обобщающий урок по механике (10 класс) Применение ядерной энергии: проблемы и перспективы
Применение ядерной энергии: проблемы и перспективы изические основы микроэлектроники
изические основы микроэлектроники Судостроение. Что общего у предметов?
Судостроение. Что общего у предметов? Презентация на тему Способы теплопередачи
Презентация на тему Способы теплопередачи  Выращивание кристаллов Учитель физики МОУ «Тюбукская СОШ №3» Каслинского муниц
Выращивание кристаллов Учитель физики МОУ «Тюбукская СОШ №3» Каслинского муниц Презентация для диплома
Презентация для диплома Тела, вещества. частиц
Тела, вещества. частиц Обобщающий урок Знатоки физики
Обобщающий урок Знатоки физики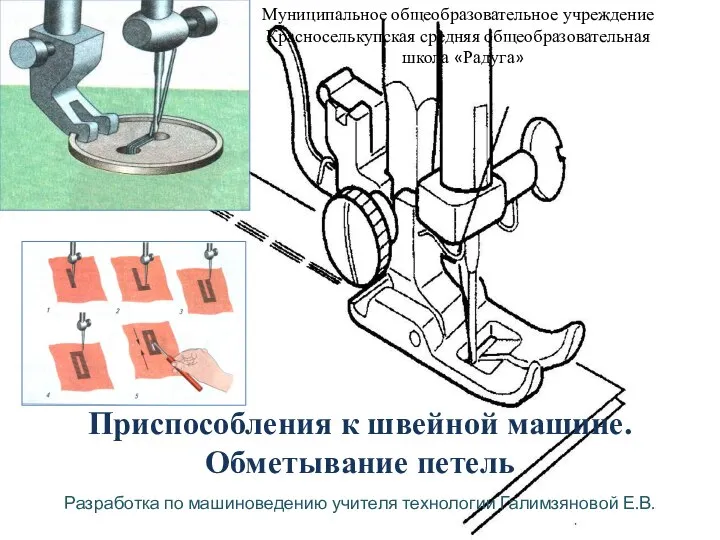 Приспособления к швейной машине. Обметывание петель
Приспособления к швейной машине. Обметывание петель Система охлаждения двигателя
Система охлаждения двигателя Порядок решения задач по динамике МТ
Порядок решения задач по динамике МТ Устройство карданной передачи, разработка технологической карты
Устройство карданной передачи, разработка технологической карты 50_ottenkov_sinego
50_ottenkov_sinego Электромагнитные волны
Электромагнитные волны Лекция 2 Высшие гармоники в трехфазных электрических цепях
Лекция 2 Высшие гармоники в трехфазных электрических цепях Лекция 23. Оптика. Волновая оптика
Лекция 23. Оптика. Волновая оптика Аморфные тела
Аморфные тела Газонаполненные фотоэлементы
Газонаполненные фотоэлементы Сложение двух сил, направленных по одной прямой. Равнодействующая сила
Сложение двух сил, направленных по одной прямой. Равнодействующая сила Презентация на тему Оптические приборы
Презентация на тему Оптические приборы  التداخل والحيود
التداخل والحيود Электромагнитные колебания. Колебательный контур 2022 дистант
Электромагнитные колебания. Колебательный контур 2022 дистант