Содержание
- 2. Криволинейное движение Криволинейное движение тел, которые в данных условиях движения можно принять за материальные точки, часто
- 3. Катасонова Н., МОУ Аннинский лицей Пример 1. Самолёты в небе.
- 4. Катасонова Н., МОУ Аннинский лицей Пример 2. Движение по горному серпантину.
- 5. Катасонова Н., МОУ Аннинский лицей Пример 3. Аттракцион «Американские горки».
- 6. Катасонова Н., МОУ Аннинский лицей Пример 4. Аттракцион в аквапарке.
- 7. Катасонова Н., МОУ Аннинский лицей Пример 5. Движение по велотреку.
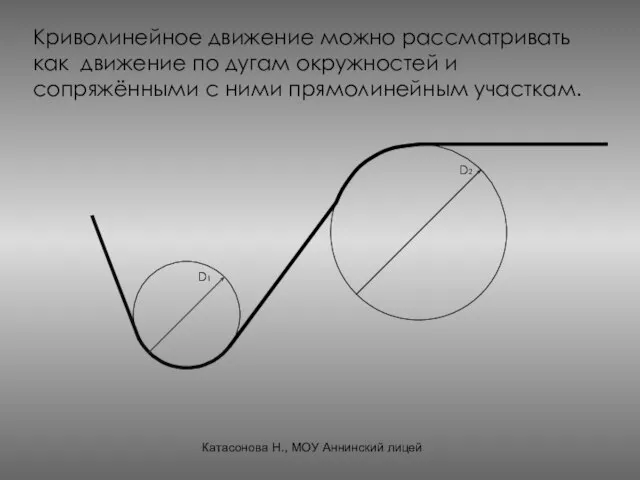
- 8. Криволинейное движение можно рассматривать как движение по дугам окружностей и сопряжёнными с ними прямолинейным участкам. D1
- 9. Не менее распространено движение по окружности. Скорость движения может оставаться постоянной по величине: практически с постоянной
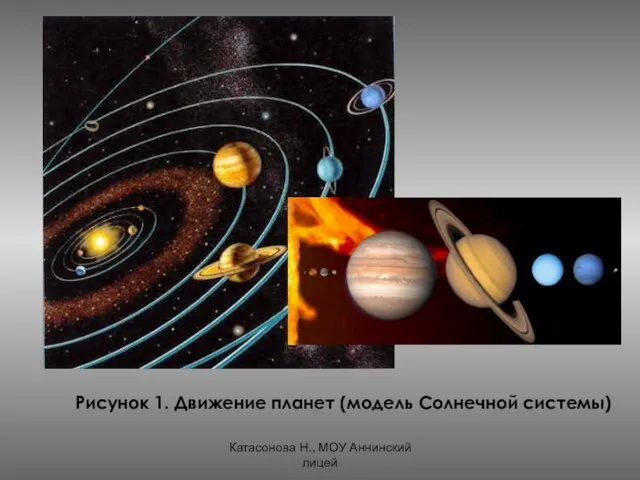
- 10. Катасонова Н., МОУ Аннинский лицей Рисунок 1. Движение планет (модель Солнечной системы)
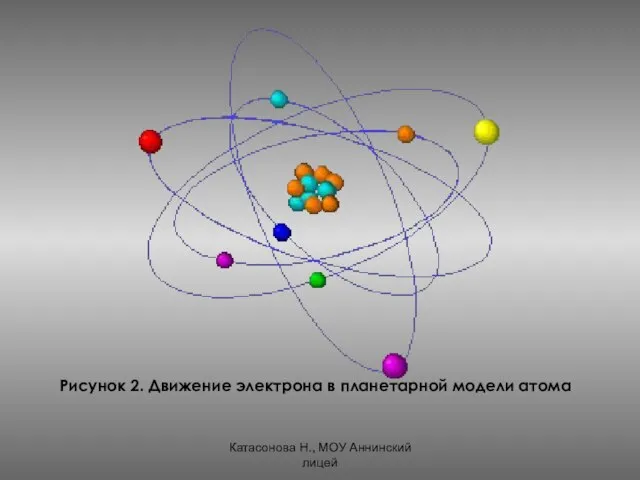
- 11. Катасонова Н., МОУ Аннинский лицей Рисунок 2. Движение электрона в планетарной модели атома
- 12. Катасонова Н., МОУ Аннинский лицей Рисунок 4. Карусель.
- 13. Катасонова Н., МОУ Аннинский лицей Рисунок 3. Работающие аттракционы.
- 14. Катасонова Н., МОУ Аннинский лицей Рисунок 5. Синхротрон Soleil, Париж.
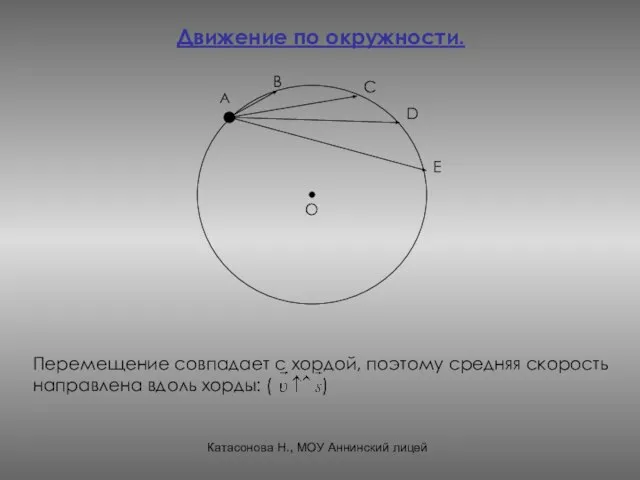
- 15. Движение по окружности. А Перемещение совпадает с хордой, поэтому средняя скорость направлена вдоль хорды: ( )
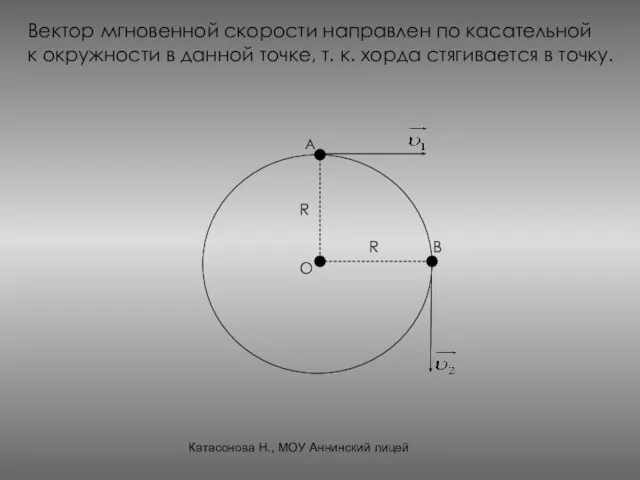
- 16. Вектор мгновенной скорости направлен по касательной к окружности в данной точке, т. к. хорда стягивается в
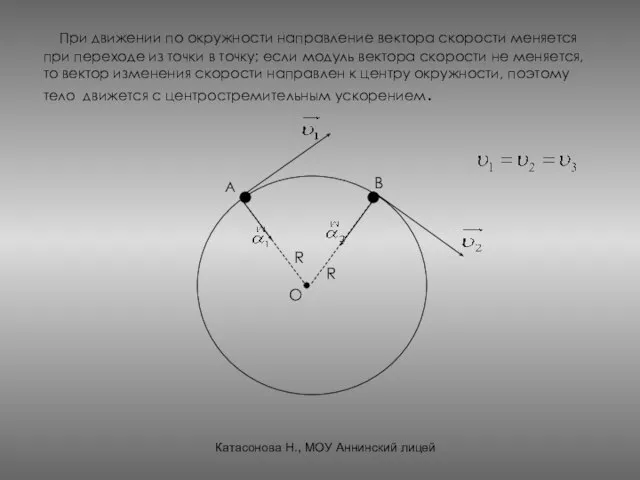
- 17. При движении по окружности направление вектора скорости меняется при переходе из точки в точку; если модуль
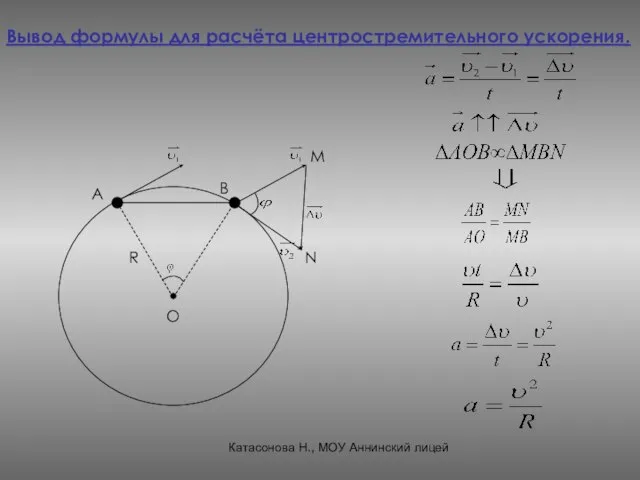
- 18. О А В М N R Вывод формулы для расчёта центростремительного ускорения. Катасонова Н., МОУ Аннинский
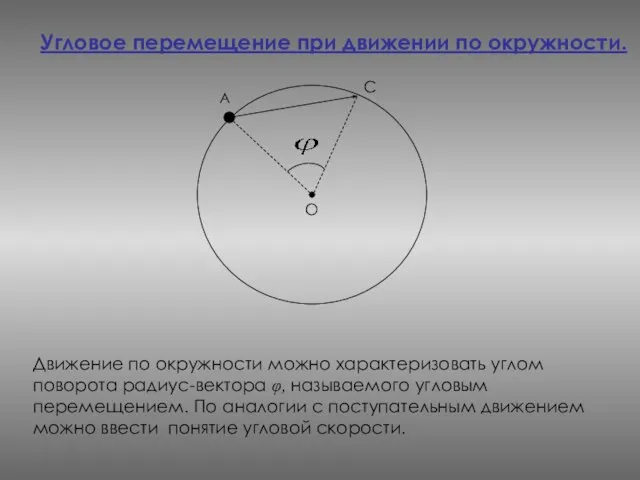
- 19. Угловое перемещение при движении по окружности. А Движение по окружности можно характеризовать углом поворота радиус-вектора φ,
- 20. Описание вращательного движения. Линейная скорость. Угловая скорость. t – время; N – число оборотов. Т –
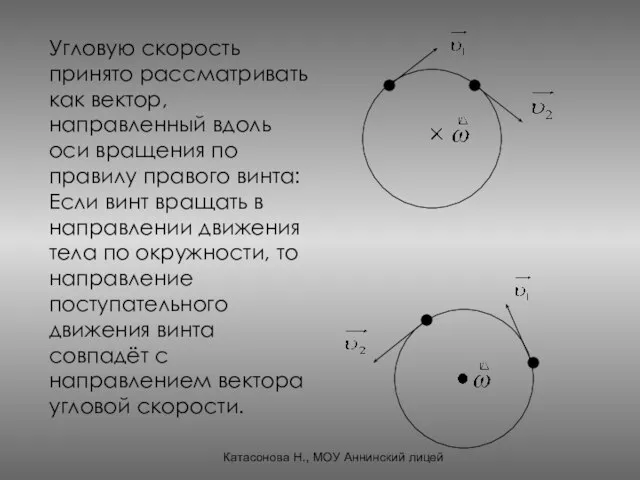
- 21. Катасонова Н., МОУ Аннинский лицей Угловую скорость принято рассматривать как вектор, направленный вдоль оси вращения по
- 22. Связь линейной и угловой скоростей. А О R При вращательном движении точек, лежащих на одном радиусе,
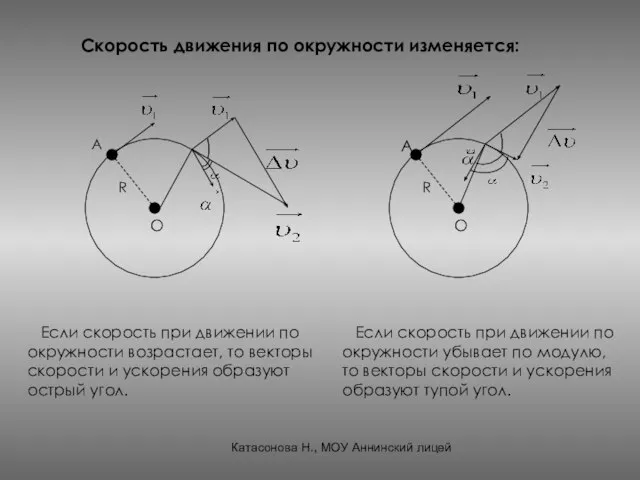
- 23. Скорость движения по окружности изменяется: А О R Если скорость при движении по окружности возрастает, то
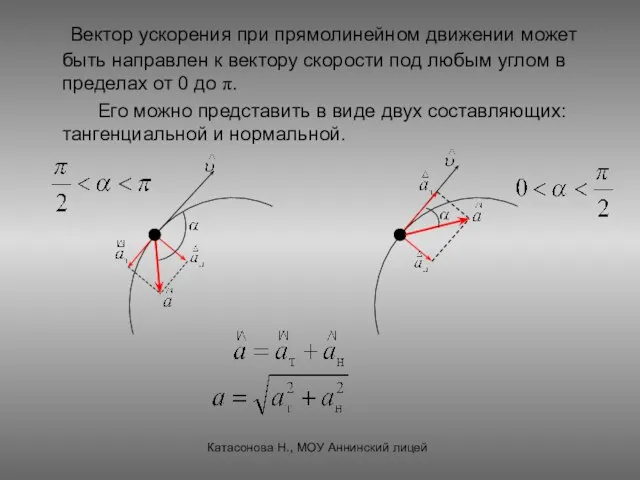
- 24. Вектор ускорения при прямолинейном движении может быть направлен к вектору скорости под любым углом в пределах
- 25. Нормальное (центростремительное) ускорение ан характеризует изменение вектора линейной скорости по направлению и направлено перпендикулярно вектору скорости
- 26. Классификация движений. прямолинейное равноускоренное прямолинейное равнозамедленное движение по окружности с постоянной по модулю скоростью криволинейное с
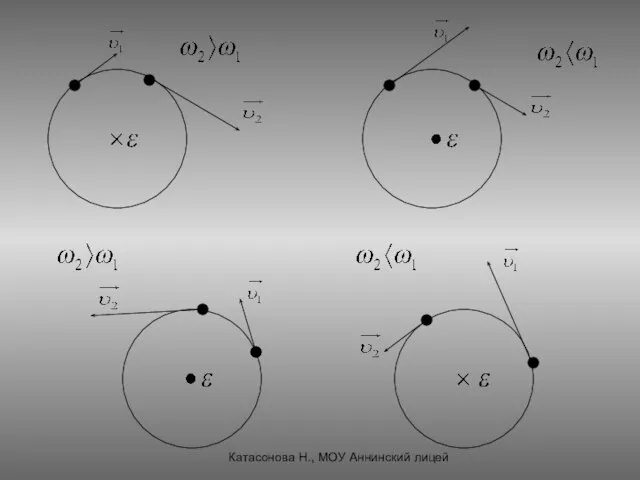
- 27. Угловое ускорение. Угловое ускорение - векторная физическая величина. Направление вектора углового ускорения определяется правилом буравчика с
- 28. Катасонова Н., МОУ Аннинский лицей
- 29. Сравнительная таблица Катасонова Н., МОУ Аннинский лицей
- 30. Вращательное движение твёрдых тел – тоже распространённый вид механического движения. Вращаются пропеллеры самолётов и гребные винты
- 31. Катасонова Н., МОУ Аннинский лицей Примеры вращательного движения твёрдых тел
- 33. Скачать презентацию


















 Механические колебания и волны. Звук
Механические колебания и волны. Звук Тормозные системы
Тормозные системы Топливо будущего
Топливо будущего Презентация на тему Интерференция. Дифракция
Презентация на тему Интерференция. Дифракция  Механическое движение
Механическое движение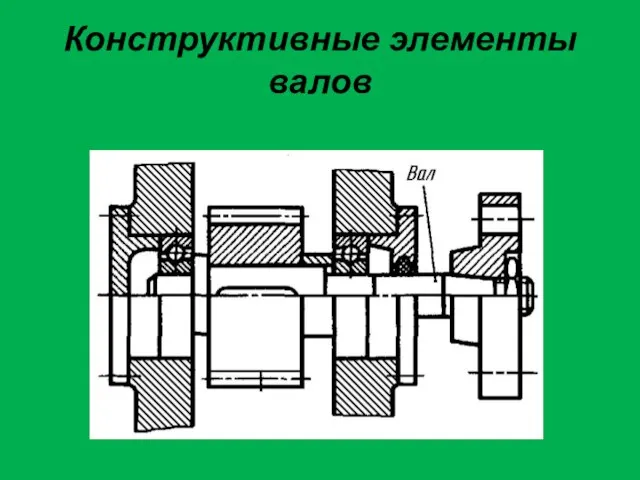 Конструктивные элементы валов
Конструктивные элементы валов Презентация на тему Выяснение условия равновесия рычага
Презентация на тему Выяснение условия равновесия рычага 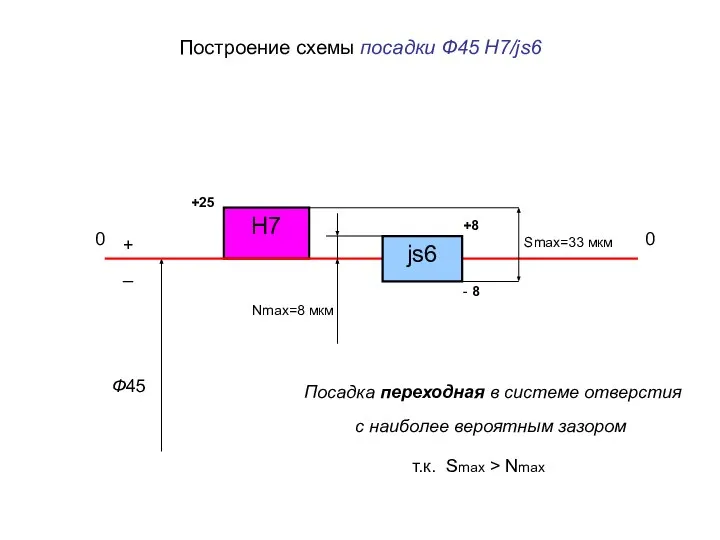 Построение схемы посадки Ф45 H7/js6
Построение схемы посадки Ф45 H7/js6 Дифракци ясвета
Дифракци ясвета Ядерное оружие
Ядерное оружие Физика плазмы
Физика плазмы Самоіндукція. Індуктивність. Енергія магнітного поля
Самоіндукція. Індуктивність. Енергія магнітного поля Электроосветительные приборы. Лампы накаливания и регулировка освещенности
Электроосветительные приборы. Лампы накаливания и регулировка освещенности Лень – двигатель прогресса или труженики с вековым стажем
Лень – двигатель прогресса или труженики с вековым стажем Длина пути машинки с крутой и пологой горки
Длина пути машинки с крутой и пологой горки Испытание цикличной нагрузки на порог-площадку
Испытание цикличной нагрузки на порог-площадку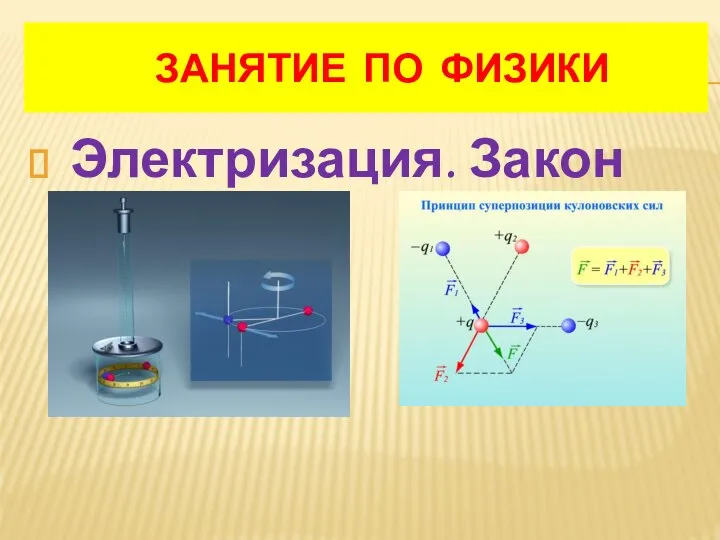 Электризация. Закон Кулона
Электризация. Закон Кулона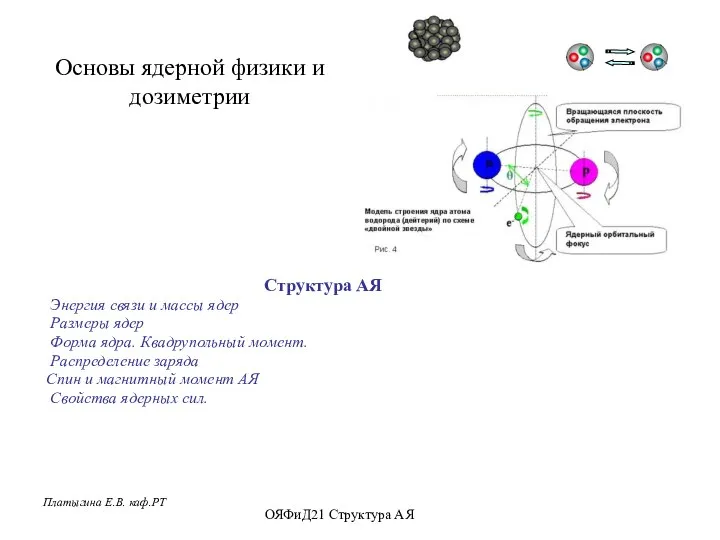 Основы ядерной физики и дозиметрии
Основы ядерной физики и дозиметрии Мастер-Кулибин из деревни Бурундуки Герасимов Артур Николаевич
Мастер-Кулибин из деревни Бурундуки Герасимов Артур Николаевич Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова
Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова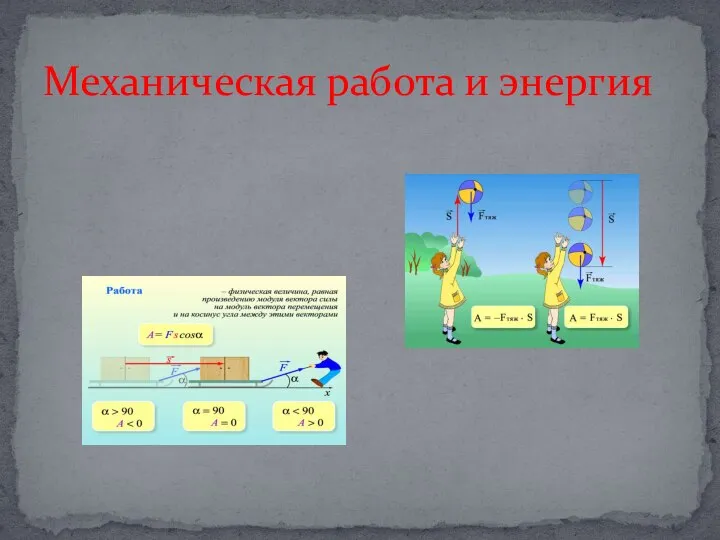 Механическая работа и энергия
Механическая работа и энергия Работа и мощность электрического тока
Работа и мощность электрического тока Фундаментальные физические величины. Упражнения. Часть 2
Фундаментальные физические величины. Упражнения. Часть 2 Проект “Голограмма”
Проект “Голограмма” изические основы микроэлектроники
изические основы микроэлектроники Механическое движение
Механическое движение Полупроводники. Собственная проводимость полупроводников
Полупроводники. Собственная проводимость полупроводников Презентация на тему Вращательное движение
Презентация на тему Вращательное движение