Техническая термодинамика

начала термодинамики
Первое начало выражает закон сохранения энергии — всеобщий закон природы. Оно определяет баланс энергии при взаимодействиях внутри термодинамической системы, а также между термодинамической системой и окружающей средой.
Второе начало определяет направленность энергетических превращений и существенно расширяет возможности термодинамического метода.
Оба начала носят опытный характер и применимы ко всем термодинамическим системам.

Термодинамические параметры
Объем V характеризуют пространство, занимаемое термодинамической системой. Он тесно связан с параметрами энергетического взаимодействия.
Часто вместо полного объема V используют объем единицы массы вещества m
Удельный объем не зависит от количества вещества и связан только с термодинамическим состоянием системы

Термодинамические параметры

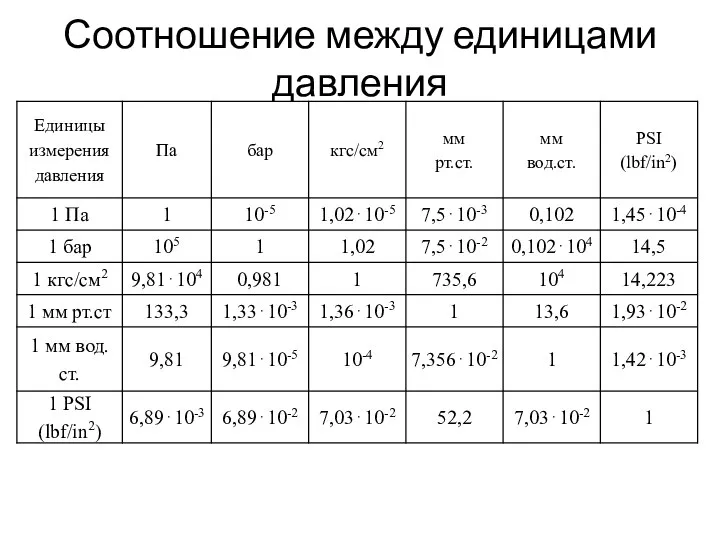
Соотношение между единицами давления

термодинамические параметры
Температура Т- в термодинамике считают мерой нагретости тела.

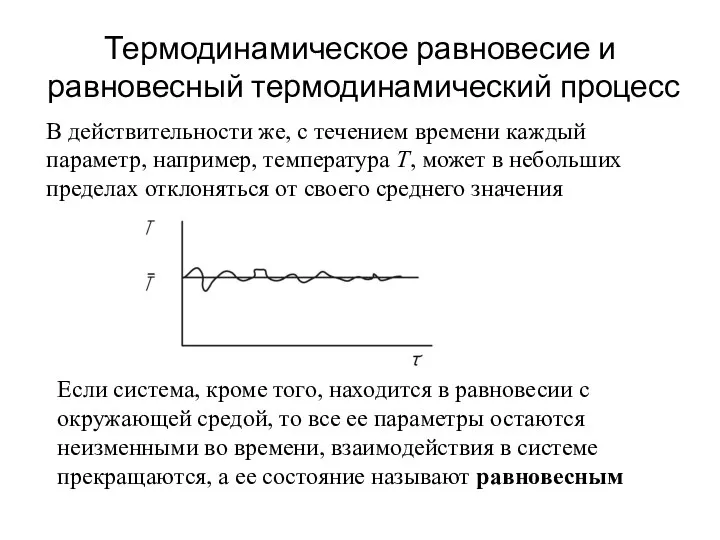
Термодинамическое равновесие и равновесный термодинамический процесс
В действительности же, с течением времени каждый параметр, например, температура Т, может в небольших пределах отклоняться от своего среднего значения
Если система, кроме того, находится в равновесии с окружающей средой, то все ее параметры остаются неизменными во времени, взаимодействия в системе прекращаются, а ее состояние называют равновесным

Термодинамическое равновесие и равновесный термодинамический процесс
Все процессы разделяют на равновесные и неравновесные.
Равновесным называют процесс, представляющий собой последовательность равновесных состояний термодинамической системы, т. е. процесс, в каждой "точке" которого система находится в равновесии.
Если же при изменении состояния равновесие в системе нарушается, процесс становится неравновесным.

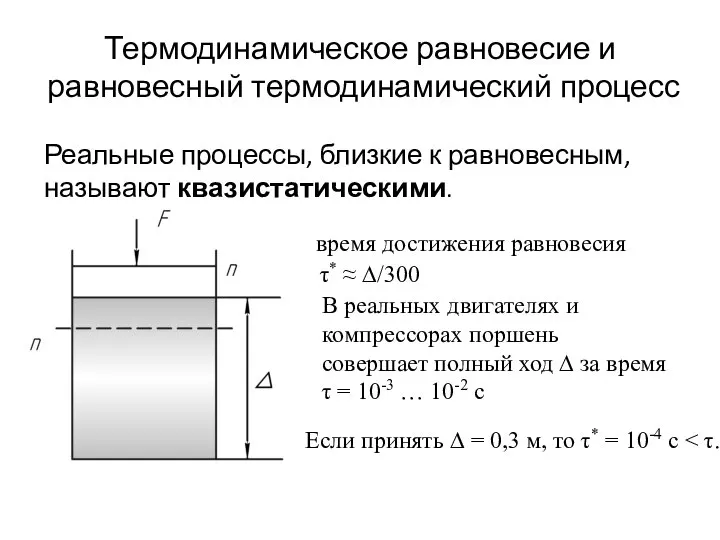
Термодинамическое равновесие и равновесный термодинамический процесс
Реальные процессы, близкие к равновесным, называют квазистатическими.
время достижения равновесия
τ* ≈ ∆/300
В реальных двигателях и компрессорах поршень совершает полный ход ∆ за время τ = 10-3 … 10-2 с
Если принять ∆ = 0,3 м, то τ* = 10-4 с < τ.

Термическое уравнение состояния
В однородных термодинамических системах любые два термических параметра однозначно определяют третий, а вся их совокупность задает состояние термодинамической системы в целом.
F(p,v,T) = 0.
Так, при давлении p = 0,1 МПа и при температуре t = 120 0C термодинамическая система представляет собой пар,
при давлении p = 5,0 МПа и t = 120 0C мы имеем дела с жидкостью
при p = 0,2 МПа вещество превратится в смесь жидкости и пара переменного состава
три равенства можно объединить

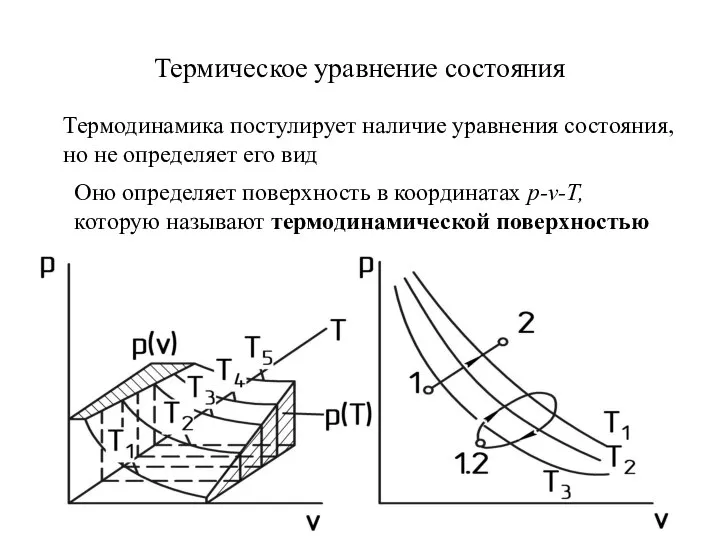
Термическое уравнение состояния
Термодинамика постулирует наличие уравнения состояния, но не определяет его вид
Оно определяет поверхность в координатах p-ν-T, которую называют термодинамической поверхностью

Законы для идеального газа
Уравнение формально объединяет три закона
закон Гей-Люссака
закон Бойля- Мариотта
закон Шарля
Идеальный газ подчиняется уравнению Клайперона – Менделеева
Ru – универсальная газовая постоянная

Смеси идеальных газов
Смесь подчиняется уравнению Клапейрона-Менделеева для смеси
Величину pmix определяет закон Дальтона
Поскольку модель идеального газа пренебрегает размерами микрочастиц, объем, занимаемый каждым компонентом, равен объему всей смеси

Смеси идеальных газов
Для каждого компонента можно использовать уравнение Клапейрона-Менделеева
Зададим состав смеси массовыми долями компонентов

Смеси идеальных газов
Левые части уравнений одинаковы, поэтому должны быть одинаковы и правые
Разделим обе части уравнения на mmix, получим
кажущаяся молярная масса
газовая постоянная

Энергия, работа, теплота
Для замкнутых систем, изучаемых термодинамикой, важно
выделить энергию термодинамической системы в целом
(кинетическую и потенциальную), которую принято называть
внешней энергией; все другие виды энергии, связанные с
движением микрочастиц, назовем внутренней энергией
системы.
Часто система неподвижна и не меняет своей потенциальной энергии, в этом случае внутренняя энергия приобретает особое значение и полностью характеризует энергетическое состояние системы.
Внутреннюю энергию системы обозначим через Е, а удельную внутреннюю энергию (отнесенную к массе системы т)— через e=E/m.

Энергия, работа, теплота
Существуют два вида взаимодействия термодинамических
систем друг с другом или с окружающей средой: путем
совершения работы и путем передачи теплоты.
Если одна система воздействует на другую и при этом происходит передача энергии, связанная с некоторым макроскопически упорядоченным процессом, то говорят, что первая система совершает над второй работу
Если же взаимодействие не приводит к макроскопически упорядоченному процессу, т. е. работа не совершается, то говорят о передаче теплоты.
Теплота и работа появляются только в процессах взаимодействия термодинамических систем

Энергия, работа, теплота
Работа, совершаемая всей системой- L
работа, совершаемая единицей массы рабочего тела - удельная работа
-работа и теплота являются функциями процесса.
-энергия — функция состояния
Работу термодинамической системы будем считать положительной (l > 0), если она совершается над другой системой или над окружающей средой
Если окружающая среда или другая термодинамическая система совершают работу над “нашей” системой, то работа отрицательна (l< 0).

Энергия, работа, теплота
Теплота - Q
Удельная теплота — теплота, приходящаяся на единицу массы:
Если термодинамическая система получает теплоту извне,
то q > 0, и наоборот, если система отдает теплоту другой
системе или окружающей среде, то q < 0.
В некоторых процессах все взаимодействие термодинамической
системы с другими системами и с окружающей средой сводится
только к совершению работы, а отдаваемая или воспринимаемая
системой теплота равна нулю. Такую термодинамическую
систему называют адиабатической, а процессы, протекающие
в ней — адиабатными.

Теплоемкость
истинная полная теплоемкость
Сх - функция процесса
Удельная теплоемкость, т. е. теплоемкость единицы массы, объема- Удельная массовая теплоемкость
Удельная мольная теплоемкость

Теплоемкость
схт
- среднее значение (от англ, middle — средний)
применим теорему о среднем и получим

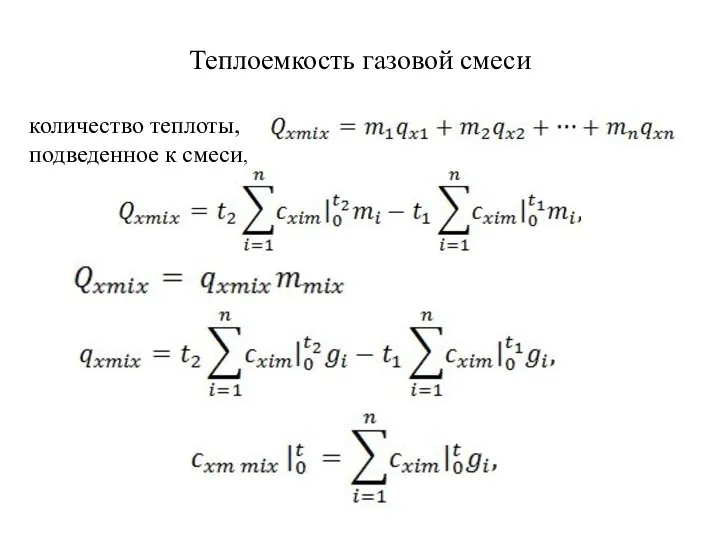
Теплоемкость газовой смеси
количество теплоты,
подведенное к смеси,

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первым началом термодинамики является закон сохранения энергии для термодинамических систем:
«в любых процессах энергия не исчезает и не создается, а лишь переходит из одного вида в другой».
подведенная к термодинамической системе теплота расходуется на изменение внутренней энергии системы и на совершение работы
∆е = q-l или q=∆е +l
Если взаимодействие с окружающей средой приводит термодинамическую систему из состояния 1 в состояние 2, то для процесса 1-2 равенство примет вид
q1-2=∆е1-2+l1-2 ∆e1-2 = e2 - e1

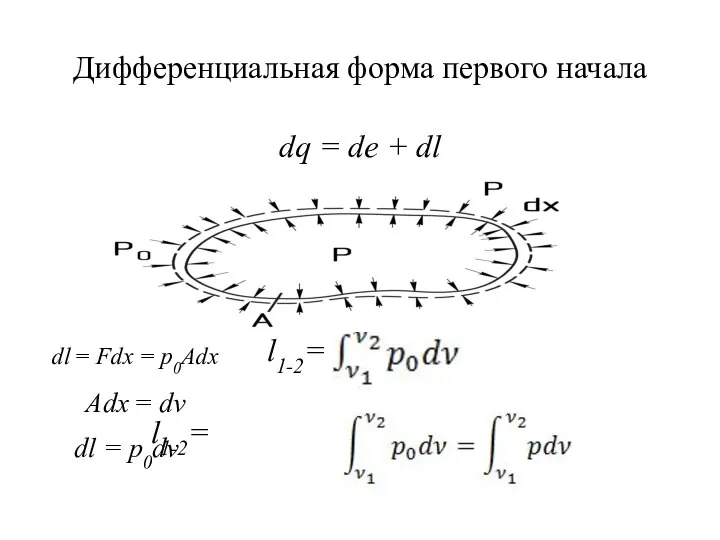
Дифференциальная форма первого начала
dq = de + dl
l1-2=
l1-2=
dl = Fdx = p0Adx
Adx = dν
dl = p0dν

p-v рабочая диаграмма состояний
пл. с1a2d =

Внутренняя энергия как функция состояния
Калорическое уравнение состояния е = е (v,Т)
Применительно к внутренней энергии е эти свойства таковы.
- Дифференциал функции состояния е является полным дифференциалом:
-Интеграл по замкнутому контуру от функции состояния е равен нулю:
-Все функции состояния являются аддитивными: если термодинамическая система состоит из п “подсистем” с внутренними энергиями еi ,то внутренняя энергия всей системы.

Энтальпия и ее свойства
тело в форме цилиндра объемом
ν = f∆
lo – работа «проталкивания» тела;
pf – усилие «проталкивания»;
∆ - перемещение тела
h=e+pv - удельная энтальпия
H=E+pV полная энтальпия

Энтальпия и ее свойства
В дифференциальной форме dh=de+d(pv)
Энтальпию удобно задавать в виде h=h(p, T)
Полный дифференциал энтальпии
Изменение энтальпии в цикле
Энтальпия – аддитивная функция:
dq=dh-d(pv)+pdv=dh-νdp

Энтальпия и ее свойства
Уравнения первого начала
В изохорном процессе (ν=const, dν = 0)
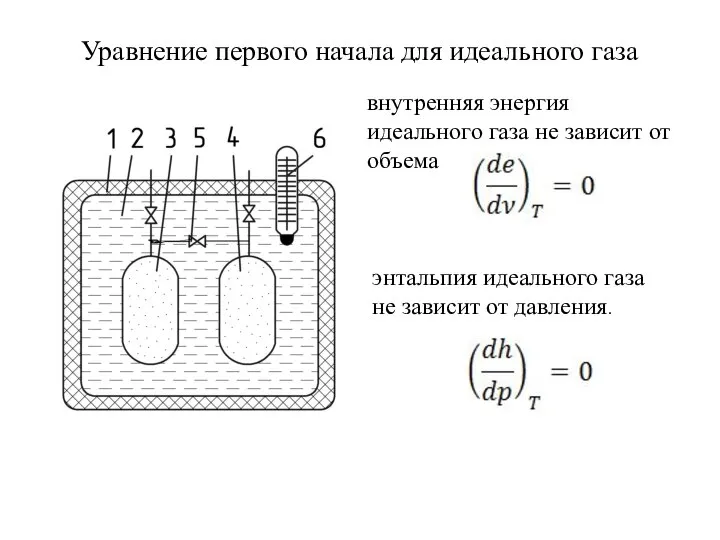
В изобарном процессе (p=const, dp = 0)

Уравнение первого начала для идеального газа
внутренняя энергия идеального газа не зависит от объема
энтальпия идеального газа не зависит от давления.

Калорические уравнения состояния идеального газа
полные дифференциалы внутренней энергии и энтальпии для идеальных газов
удельная изобарная теплоемкость газа больше его удельной изохорной теплоемкости на величину газовой постоянной. (формула Майера)
Уравнение первого начала для идеального газа

АНАЛИЗ ПРОЦЕССОВ С ИДЕАЛЬНЫМ ГАЗОМ. Изобарный процесс
при dp=0
dh =cpdT
Связь термических параметров газа в любых двух точках 1 и 2 такого процесса задается законом Гей-Люссака:
qp1-2
ср (T2 - T1).

Изохорный процесс
Работа газа в изохорном процессе равна нулю, поскольку dν=0
Если теплоемкость
слабо зависит от температуры
qν1-2
сv (T2 - T1)
Термические параметры изохорного процесса 1-2 определяются законом Шарля:

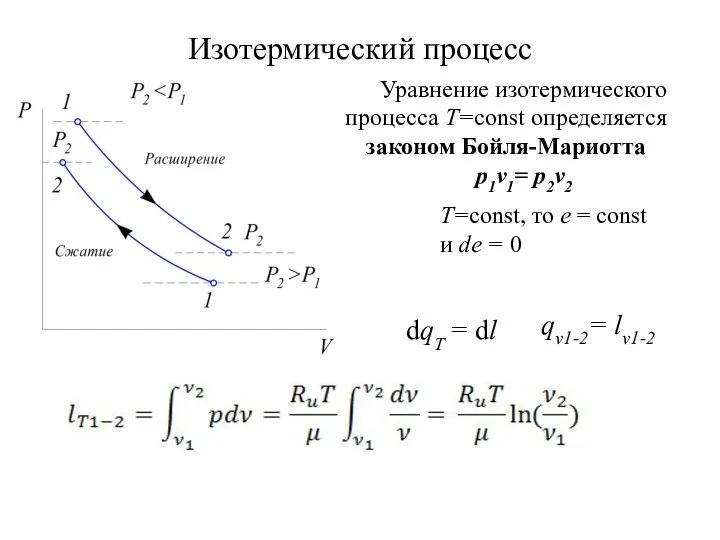
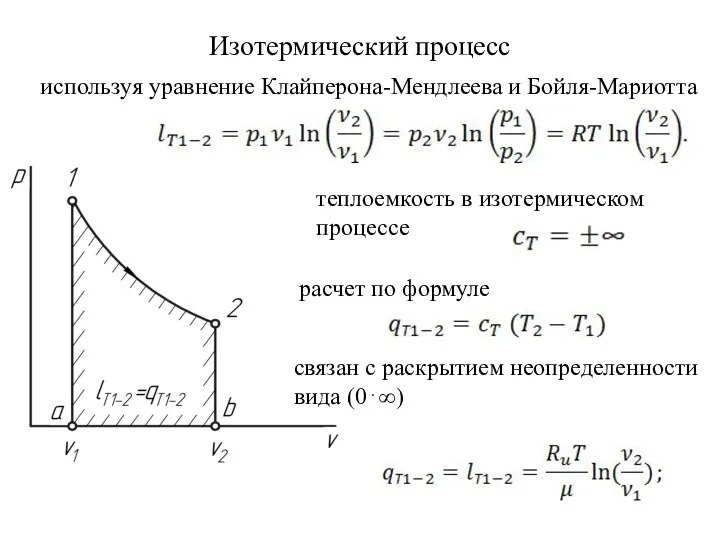
Изотермический процесс
Т=const, то е = const и de = 0
dqT = dl
qν1-2= lν1-2
Уравнение изотермического процесса Т=const определяется законом Бойля-Мариотта
p1ν1= p2ν2

Изотермический процесс
используя уравнение Клайперона-Мендлеева и Бойля-Мариотта
теплоемкость в изотермическом процессе
расчет по формуле
связан с раскрытием неопределенности вида (0⋅∞)

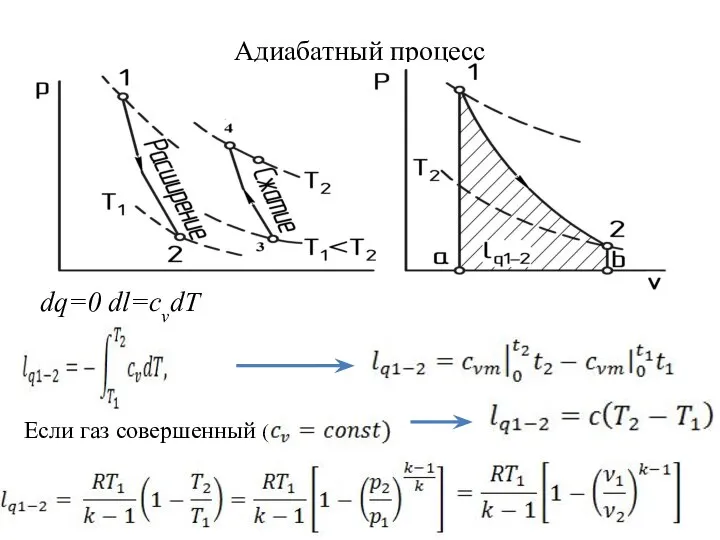
Адиабатный процесс
Для идеального газа dh = срdT,
при dq=0 и q1-2=0 уравнение первого начала принимает вид
Для идеального газа величина
постоянна и носит название коэффициента Пуассона, или показатели адиабаты.

Адиабатный процесс
k= 1,66 для одноатомных газов;
k= 1,40 для двухатомных;
k = 1,33 для трех- и более атомных
Идеальный газ, у которого ср = const, cv = const, называют совершенным
Последовательно преобразуя формулу

Адиабатный процесс
уравнение адиабаты Пуассона
Подставим в уравнение
Аналогично можно найти связь между p и Т:
Построим кривую q=0 в рабочей диаграмме состояний.
поскольку k>1, кривая адиабатного процесса в p-v диаграмме пройдет круче изотермы

Адиабатный процесс
Если газ совершенный (
dq=0 dl=cvdT

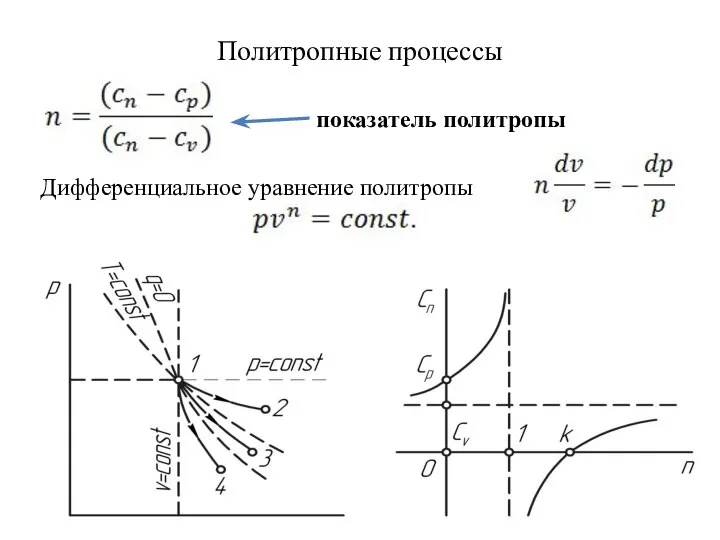
Политропные процессы
Политропные процессы — процессы идеальною газа, идущие при постоянной теплоемкости
Кроме того, при cv=const
или в интегральной форме для процесса 1-2
в политропных процессах доля теплоты, переходящая в работу, постоянна

Политропные процессы
Если в формулы первого начала подставить значение q=
откуда следует, что
После почленного деления получим

Политропные процессы
Дифференциальное уравнение политропы
показатель политропы

Политропные процессы
Процессам:
p=const n=0, T=const n=1
v=const n = q =сonst n=k
,
для процесса 1-2 0
Работа политропного процесса

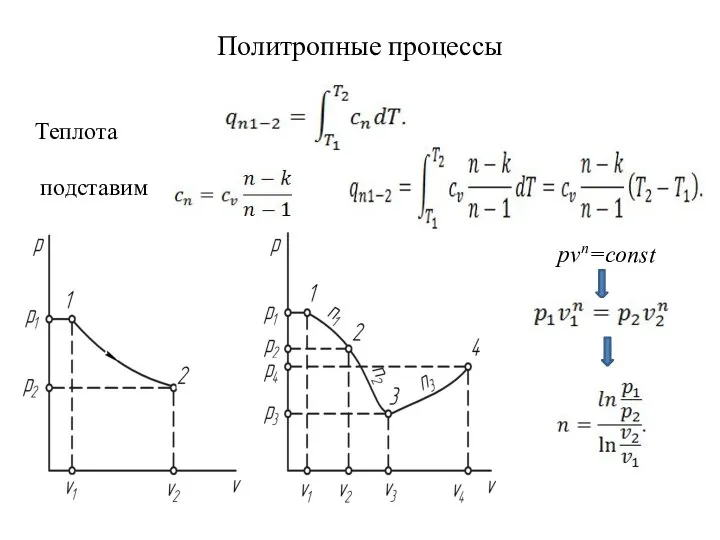
Политропные процессы
Теплота
подставим
pvn=const

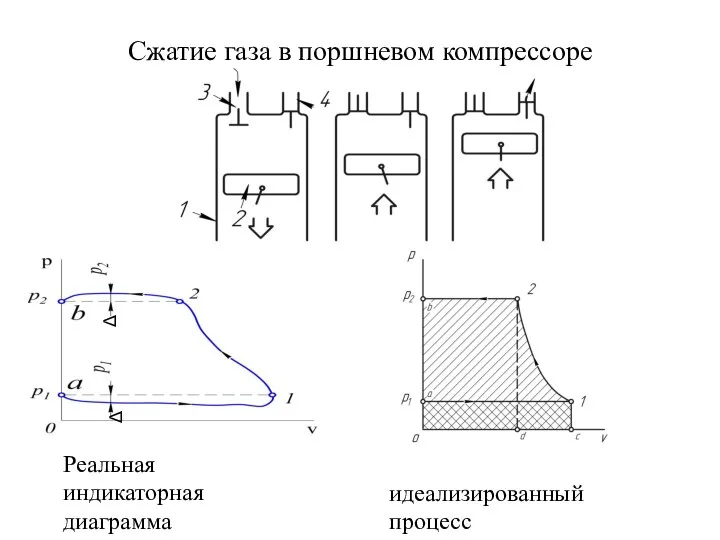
Сжатие газа в поршневом компрессоре
Реальная индикаторная диаграмма
идеализированный процесс
Δ
Δ

Сжатие газа в поршневом компрессоре
Работа изобарного процесса а-1
аналогично выражается и работа процесса 2-b
Работа в процессе сжатия 1-2, характер которого пока неизвестен,
а общая работа, подводимая к газу в компрессоре,

Сжатие газа в поршневом компрессоре
Возьмем интеграл в правой части равенства по частям:
Откуда
Функция, которая учитывает не только работу основного процесса, но и энергетический вклад впуска и выпуска рабочего тела, называют технической (или располагаемой) работой.

Работа, затраченная на привод компрессора
при адиабатном сжатии,
при изотермическом сжатии