Содержание
- 2. Остроградский Михаил Васильевич (1801 – 1862), отечественный математик и механик. Учился в Харьковском ун-те (1816 –
- 3. Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик. В 1832 г. создал абсолютную
- 4. Основная ценность теоремы Остроградского-Гаусса состоит в том, что она позволяет глубже понять природу электростатического поля и
- 5. Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф через эту поверхность.
- 6. Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их
- 7. если на рисунке выделить площадку S то напряженность изображенного поля будет равна
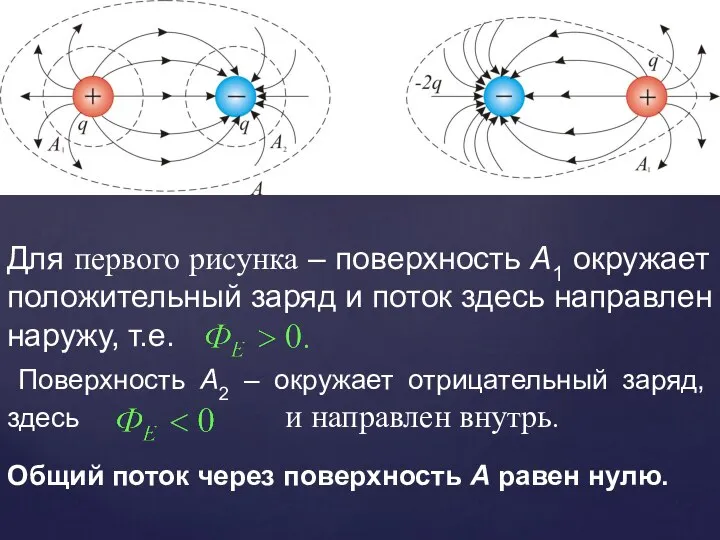
- 8. Для первого рисунка – поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е. Поверхность
- 9. Итак, по определению, поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S. 2.3.
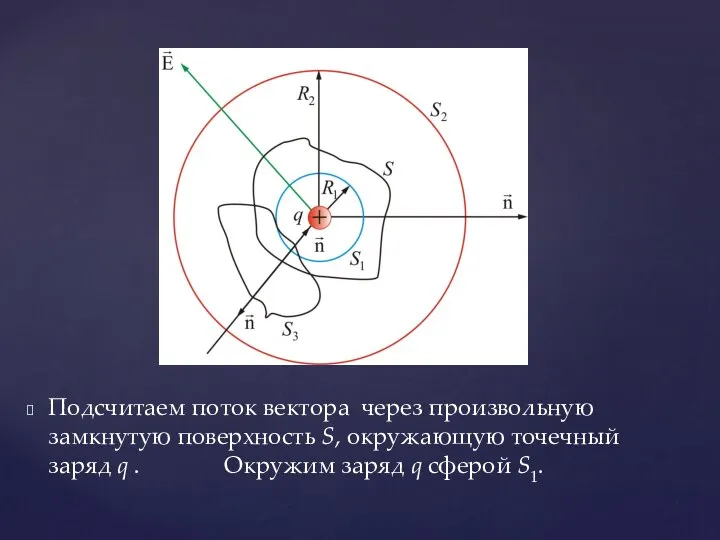
- 10. Подсчитаем поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд q . Окружим заряд q
- 11. Центр сферы совпадает с центром заряда. Радиус сферы S1 равен R1. В каждой точке поверхности S1
- 12. Тогда поток через S1
- 13. Подсчитаем поток через сферу S2, имеющую радиус R2:
- 14. Из непрерывности линии следует, что поток и через любую произвольную поверхность S будет равен этой же
- 15. Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности: – теорема Гаусса для нескольких зарядов. Поток
- 16. Полный поток проходящий через S3, не охватывающую заряд q, равен нулю:
- 17. Таким образом, для точечного заряда q, полный поток через любую замкнутую поверхность S будет равен: –
- 18. Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах пространства: Здесь dV
- 19. Суммарный заряд объема dV будет равен: Тогда из теоремы Гаусса можно получить: – это ещё одна
- 20. Пусть заряд распределен в пространстве ΔV, с объемной плотностью . Тогда 2.4. Дифференциальная форма теоремы Остроградского-Гаусса
- 21. Дивергенция поля Е Аналогично определяется дивергенция любого другого векторного поля. Из этого определения следует, что дивергенция
- 22. Итак, Это теорема Остроградского-Гаусса в дифференциальной форме. Написание многих формул упрощается, если ввести векторный дифференциальный оператор
- 23. Сам по себе оператор смысла не имеет. Он приобретает смысл в сочетании с векторной или скалярной
- 24. 2.5. Вычисление электрических полей с помощью теоремы Остроградского-Гаусса 2.5.1. Поле бесконечной однородно заряженной плоскости
- 25. Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: dq – заряд, сосредоточенный на
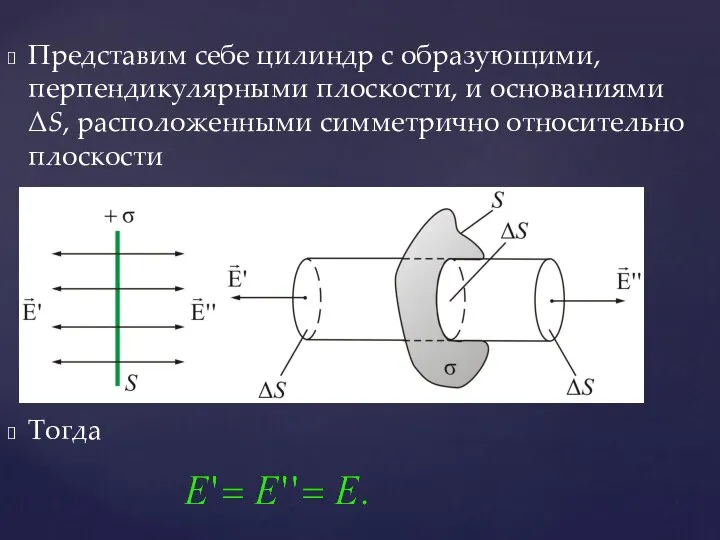
- 26. Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости Тогда
- 27. Суммарный поток через замкнутую поверхность (цилиндр) будет равен: Внутри поверхности заключён заряд . Следовательно, из теоремы
- 28. Пусть две бесконечные плоскости заряжены разноимёнными зарядами с одинаковой по величине плотностью σ 2.5.2. Поле двух
- 29. Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри
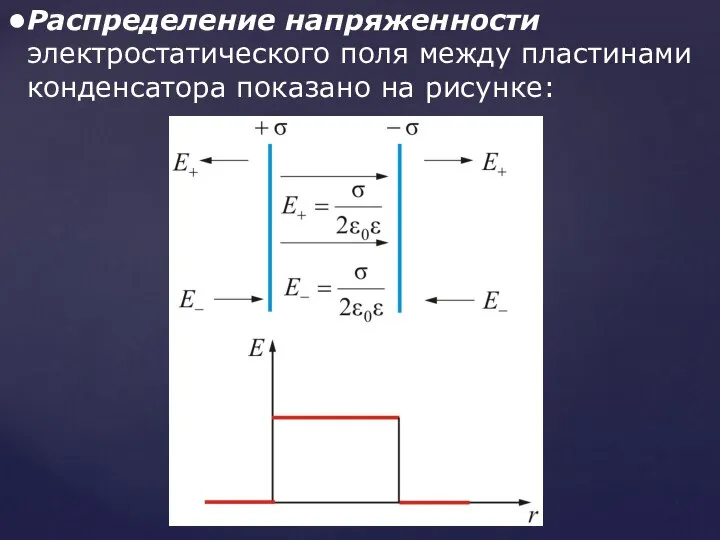
- 30. Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке:
- 31. Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин): Механические силы, действующие между заряженными
- 32. Сила притяжения между пластинами конденсатора: где S – площадь обкладок конденсатора. Т.к. Это формула для расчета
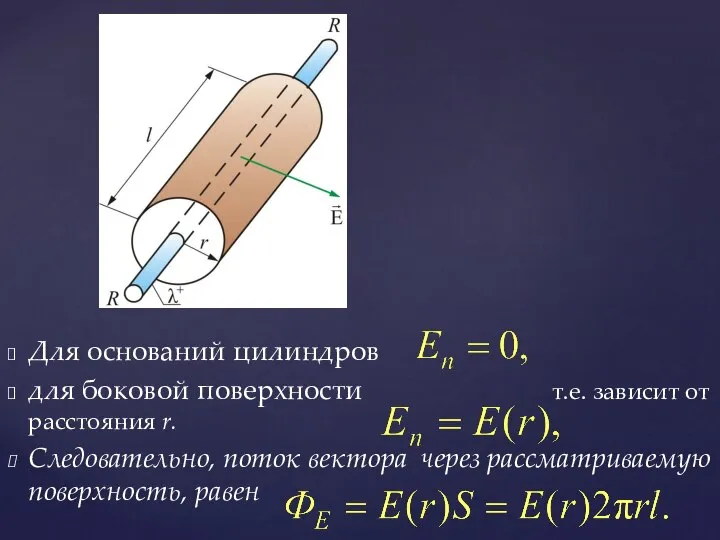
- 33. Пусть поле создаётся бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью где dq –
- 34. Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания
- 35. Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r. Следовательно, поток вектора через рассматриваемую
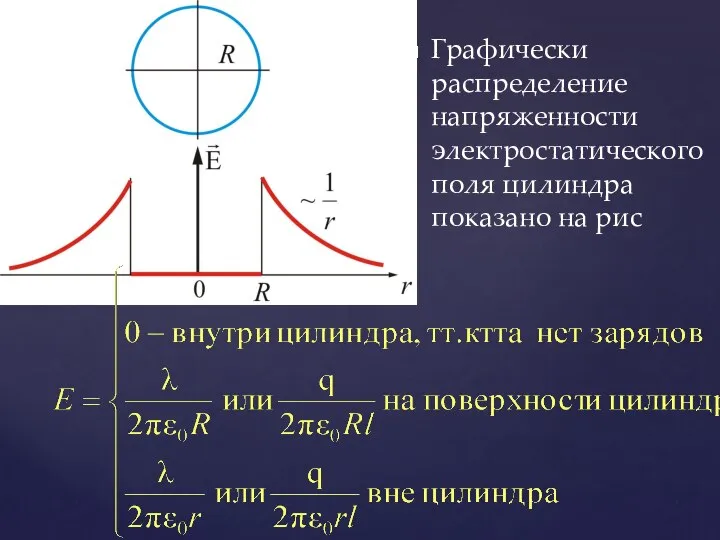
- 36. При на поверхности будет заряд По теореме Остроградского-Гаусса Тогда Если , т.к. внутри замкнутой поверхности зарядов
- 37. Графически распределение напряженности электростатического поля цилиндра показано на рис
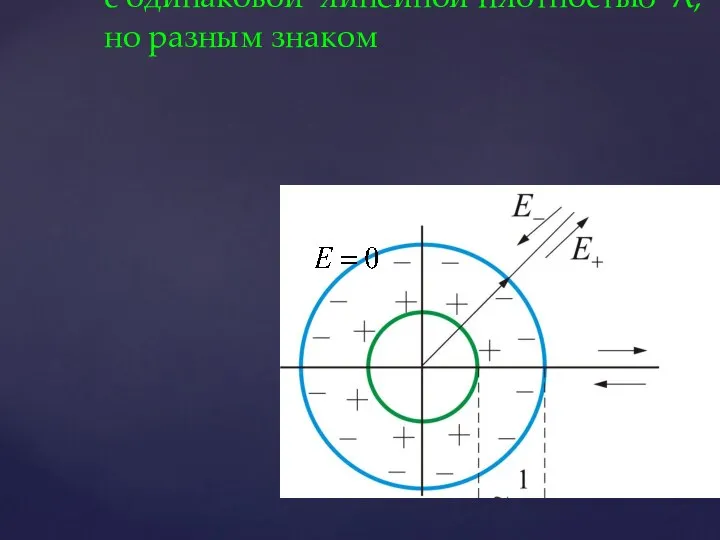
- 38. 2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
- 39. Внутри меньшего и вне большего цилиндров поле будет отсутствовать В зазоре между цилиндрами, поле определяется так
- 40. Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами
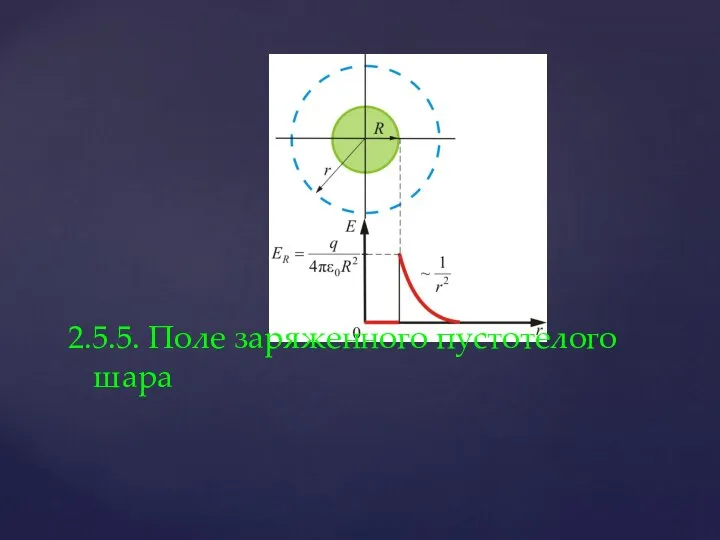
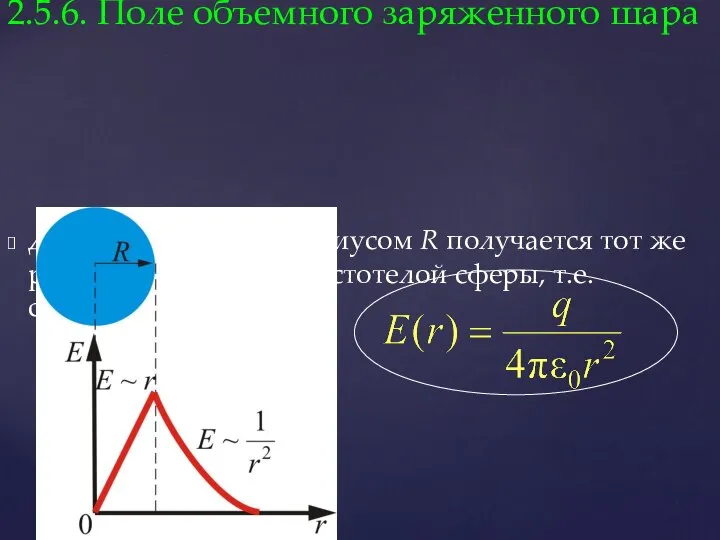
- 41. 2.5.5. Поле заряженного пустотелого шара
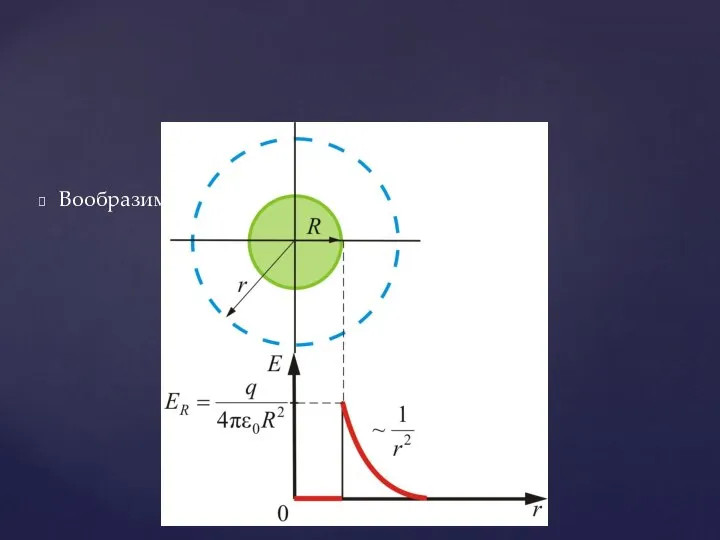
- 42. Вообразим вокруг шара – сферу радиуса r (рис).
- 43. Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда откуда поле вне
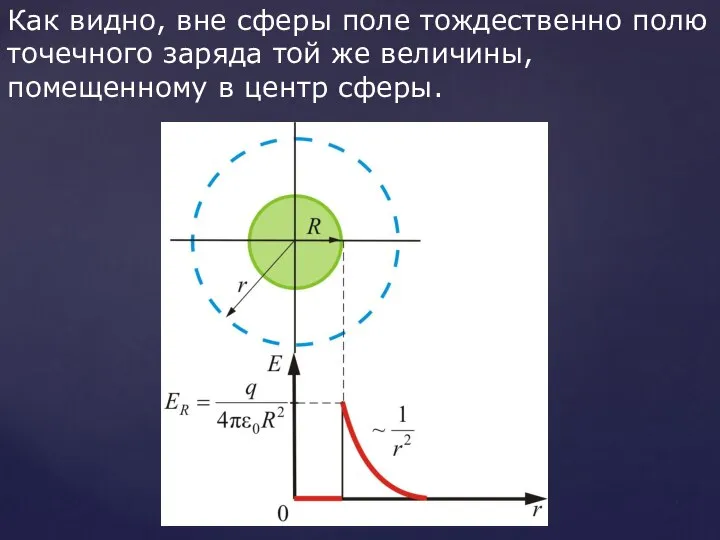
- 44. Как видно, вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
- 45. Для поля вне шара радиусом R получается тот же результат, что и для пустотелой сферы, т.е.
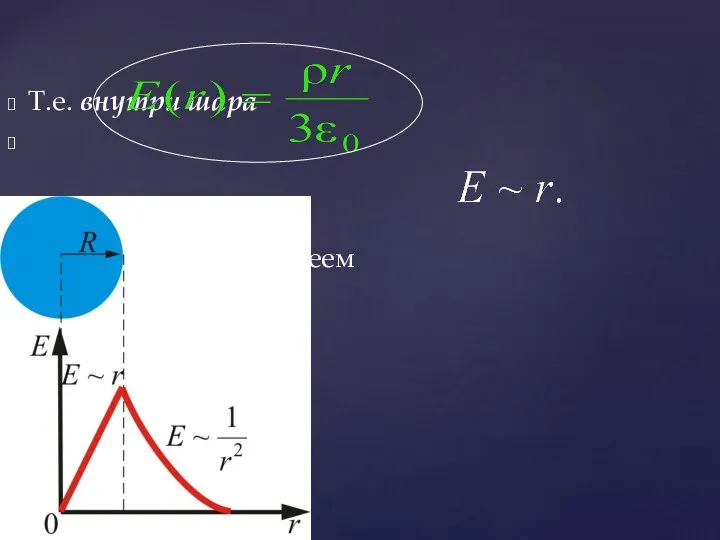
- 46. Внутри шара при сферическая поверхность будет содержать в себе заряд, равный где ρ – объемная плотность
- 47. Т.е. внутри шара Т.е., внутри шара имеем
- 48. Таким образом, имеем: поле объемного заряженного шара
- 50. Скачать презентацию



































 Влияние дефектов на физические свойства кристаллов
Влияние дефектов на физические свойства кристаллов Скорость. Расчет пути и времени движения
Скорость. Расчет пути и времени движения Механика деформируемого твердого тела
Механика деформируемого твердого тела Дифракция
Дифракция Noteikt daļiņas lādiņa zīmi pēc kreisas rokas likuma!
Noteikt daļiņas lādiņa zīmi pēc kreisas rokas likuma! Теоретические основы электротехники. Теория электромагнитного поля. Лекция 10
Теоретические основы электротехники. Теория электромагнитного поля. Лекция 10 Юные физики. Игра. 7 класс
Юные физики. Игра. 7 класс Паросиловая установка (ПСУ)
Паросиловая установка (ПСУ) Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса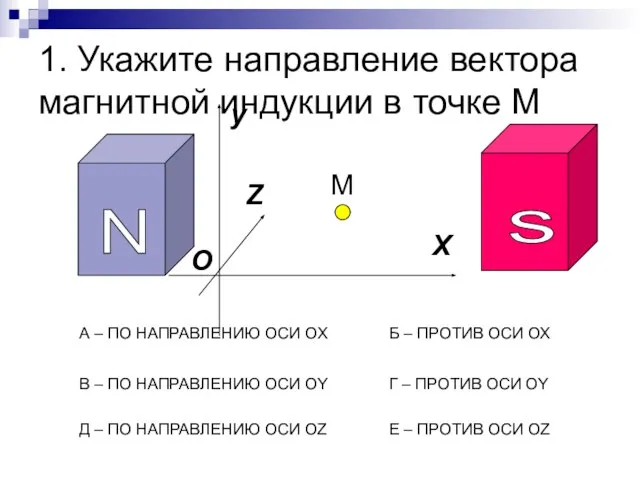 Тест по теме Электромагнетизм
Тест по теме Электромагнетизм Цепи с сопротивлением, индуктивностью, ёмкостью
Цепи с сопротивлением, индуктивностью, ёмкостью Механика. Комплексный экзамен
Механика. Комплексный экзамен Зубчатые передачи
Зубчатые передачи 1426584
1426584 Презентация на тему Низкочастотные колебания
Презентация на тему Низкочастотные колебания  Валерий Брюсов “Мир электрона”. (1922г)
Валерий Брюсов “Мир электрона”. (1922г) Первый закон термодинамики
Первый закон термодинамики Преломление света. Физический смысл показателя преломления. Электромагнитные явления
Преломление света. Физический смысл показателя преломления. Электромагнитные явления Физика атомного ядра и элементарных частиц
Физика атомного ядра и элементарных частиц Cокол тысячелетия 10,08
Cокол тысячелетия 10,08 И. Кеплер, и его вклад и развитие механики
И. Кеплер, и его вклад и развитие механики Рентгеновские лучи
Рентгеновские лучи Система пуска двигателя
Система пуска двигателя Взаимодействие тел
Взаимодействие тел Введение в предмет Микросхемотехника
Введение в предмет Микросхемотехника Освещение. Свет и тень
Освещение. Свет и тень Основы строительных конструкций. Метод предельного равновесия. Лекция 10
Основы строительных конструкций. Метод предельного равновесия. Лекция 10 Ефективність грохочення
Ефективність грохочення