Содержание
- 2. Магнитное поле постоянных токов Из полной системы уравнений электромагнитного поля используем уравнения, относящиеся к магнитному полю:
- 3. Скалярный магнитный потенциал Разность магнитных потенциалов между двумя точками определяется как линейный интеграл от вектора напряженности
- 4. Многозначность функции магнитного потенциала a p q i b k n 1. Разность магнитных скалярных потенциалов
- 5. Плоскопараллельное магнитное поле Плоскопараллельное магнитное поле создается системой параллельных весьма длинных проводов с постоянными токами.
- 6. Комплексный потенциал магнитного поля. Wm = Vm + jUm - по аналогии с электростатическим полем ΔUm
- 7. Поле уединенного проводника с током Wm = Vm + jUm = k·ln z + C1 +
- 8. Выбор значений постоянных C1 и C2 определяет положение начальных (нулевых) линий скалярного магнитного потенциала и функции
- 9. Линии напряженности магнитного поля, созданного током в круговом проводе, представляют собой окружности с центром на оси
- 10. Магнитное поле двух нитей с прямым и обратным током Комплексный магнитный потенциал в этом случае на
- 11. Магнитное поле двухпроводной линии передач постоянного тока Для проводов, имеющих конечные радиусы, магнитное поле вне этих
- 12. Магнитное поле двухпроводной линии передач постоянного тока Строить магнитное поле проводников с токами проще, чем электростатическое,
- 13. Принцип соответствия плоскопараллельных электрических и магнитных полей. Сравнивая выражения для комплексного потенциала электростатического поля в системе
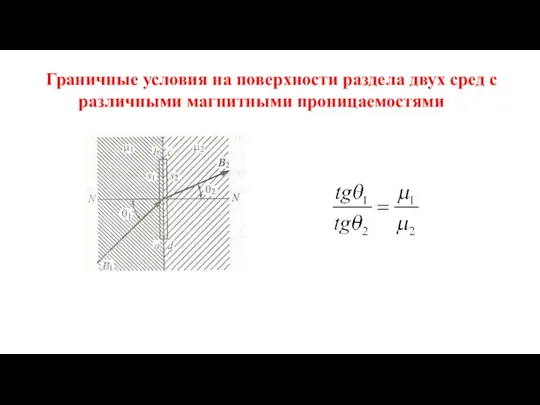
- 14. Граничные условия на поверхности раздела двух сред с различными магнитными проницаемостями
- 15. Граничные условия в магнитном поле у поверхности ферромагнетиков. Магнитная проницаемость ферромагнетиков во много раз превышает магнитную
- 16. Граничные условия в магнитном поле у поверхности ферромагнетиков. Это означает, что в воздухе у поверхности ферромагнетика
- 17. Метод зеркальных изображений в магнитном поле. Um = const μFerr μ0 μ0 μ0 Рассмотрим проводник с
- 18. Графический метод построения картины плоскопараллельного магнитного поля. В области не занятой обмотками с током При построении
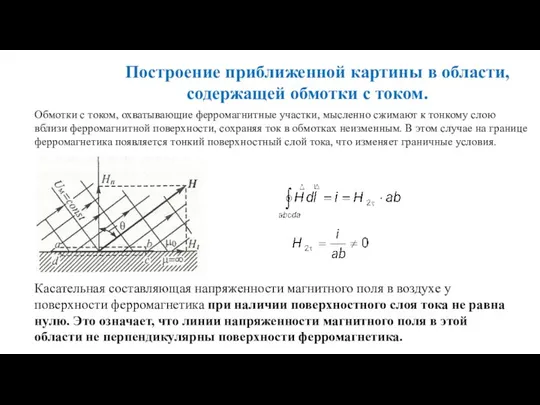
- 19. Построение приближенной картины в области, содержащей обмотки с током. Обмотки с током, охватывающие ферромагнитные участки, мысленно
- 20. Приближенные методы расчета и построения картины плоскопараллельного поля. Метод сеток. Рассмотрим его применение на примере определения
- 21. Разобьем исследуемую область с помощью линий, параллельных осям координат, на одинаковые ячейки, шириной Δx и высотой
- 22. Рассмотрев произвольный узел сетки (o) и четыре примыкающие к нему узла (a,b,c,d), можем записать через приращения
- 24. Скачать презентацию



















 Звуковые волны. Свойства звука
Звуковые волны. Свойства звука Физика вокруг нас Подготовили: обучающиеся 10 класса
Физика вокруг нас Подготовили: обучающиеся 10 класса Создание условий высокой мотивации учащихся в учебной деятельности на уроках физики
Создание условий высокой мотивации учащихся в учебной деятельности на уроках физики Механика. Теория относительности А. Эйнштейна. Постулат постоянства скорости света
Механика. Теория относительности А. Эйнштейна. Постулат постоянства скорости света Закон сохранения импульса
Закон сохранения импульса Изобретение радио А. С. Поповым
Изобретение радио А. С. Поповым Полупроводниковые приборы
Полупроводниковые приборы Влияние электромагнитного излучения на организм и здоровье человека
Влияние электромагнитного излучения на организм и здоровье человека Электричество. 8 класс
Электричество. 8 класс Механические свойства твердых тел. Деформация. Упругость. Прочность
Механические свойства твердых тел. Деформация. Упругость. Прочность Презентация на тему Постоянные магниты
Презентация на тему Постоянные магниты  Шкала и первый импульс
Шкала и первый импульс Презентация на тему ПРОБЛЕМНОЕ ОБУЧЕНИЕ на уроках ФИЗИКИ
Презентация на тему ПРОБЛЕМНОЕ ОБУЧЕНИЕ на уроках ФИЗИКИ 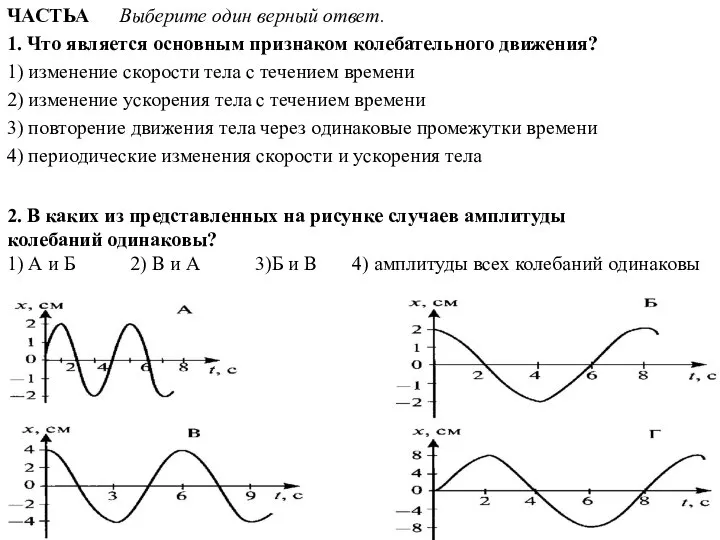 Колебательное движение (9 класс)
Колебательное движение (9 класс) Исследование фазового равновесия
Исследование фазового равновесия Сложение потенциальных потоков
Сложение потенциальных потоков Теорія лінійних систем автоматичного керування. Лекція 2
Теорія лінійних систем автоматичного керування. Лекція 2 Форма и характеристики электрических сигналов. Анализ
Форма и характеристики электрических сигналов. Анализ Реверберация. Лекция2
Реверберация. Лекция2 Газовые законы
Газовые законы Электродинамика. Решение задач
Электродинамика. Решение задач Энергия связи
Энергия связи Простые механизмы. Рычаг
Простые механизмы. Рычаг Электрический ток. Соединения проводников
Электрический ток. Соединения проводников Презентация на тему Манометр
Презентация на тему Манометр  Способ уменьшения ударов в шагающем механизме
Способ уменьшения ударов в шагающем механизме Блок контроля
Блок контроля Фотометрический анализ
Фотометрический анализ