Содержание
- 2. Метод зеркальных изображений
- 3. Используется для расчета поля заряженных проводников , расположенных вблизи плоских поверхностей, ограничивающих проводящую среду +q jy
- 4. Отразим заряд +τ1 от вертикальной стенки, вследствие чего появится второй заряд противоположного знака –τ2 , и
- 5. Метод конформных отображений
- 6. Расчет поля методом конформных отображений основан на том, что существует возможность отобразить с помощью некоторого математического
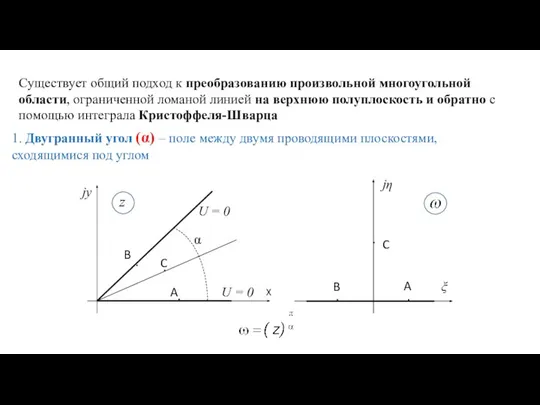
- 7. Существует общий подход к преобразованию произвольной многоугольной области, ограниченной ломаной линией на верхнюю полуплоскость и обратно
- 8. Положение точки на первой грани (точка A) : - в исходной области Z - в области
- 9. 2. Бесконечно глубокий проводящий паз шириной d jy jη A E F d B O C
- 10. Положение угловых точек B и C Положение точек A и D Положение точки E
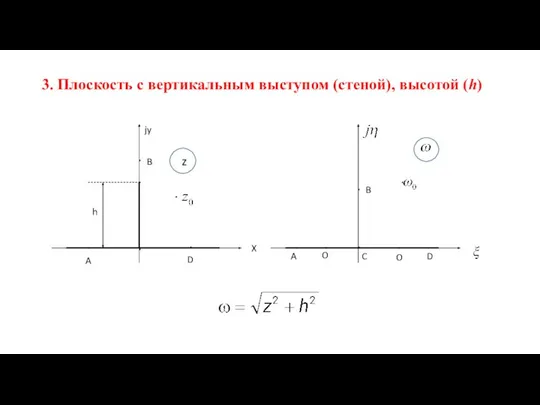
- 11. 3. Плоскость с вертикальным выступом (стеной), высотой (h) A B h D jy X A O
- 12. Положение точки C Положение точки O Положение точек A и D Положение точки B (y>h)
- 13. Комплексный потенциал и плотность заряда (σ) на примере плоскости с выступом z0 = x0 + jy0
- 14. Выразим через Z для перехода к исходной области. Напряженность электрического поля в любой точке: После упрощения:
- 16. Скачать презентацию











 Что изучает физика? Вводный урок в 7 классе
Что изучает физика? Вводный урок в 7 классе Фонтаны петергофа
Фонтаны петергофа Дисперсные системы
Дисперсные системы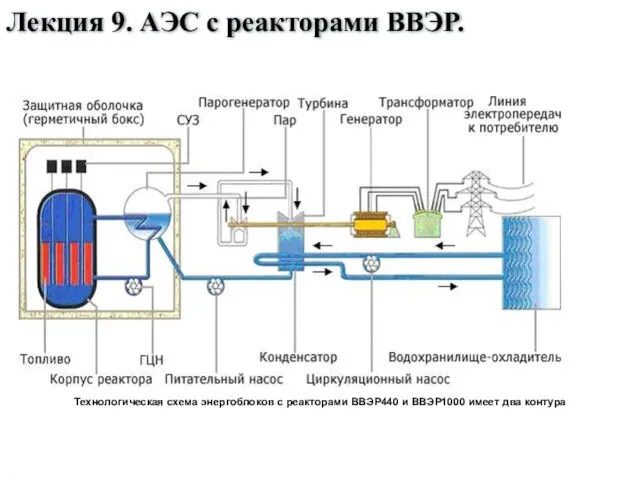 АЭС с реакторами ВВЭР. Лекция 9
АЭС с реакторами ВВЭР. Лекция 9 Дифракция света. Лекции 14-15
Дифракция света. Лекции 14-15 Дефекты и наноструктурные материалы
Дефекты и наноструктурные материалы Презентация на тему Сложение скоростей
Презентация на тему Сложение скоростей  Презентация на тему Оптические иллюзии или обман зрения
Презентация на тему Оптические иллюзии или обман зрения  Экзотические типы радиоактивного распада
Экзотические типы радиоактивного распада Кинематические характеристики механического движения
Кинематические характеристики механического движения Второй закон Ньютона, масса
Второй закон Ньютона, масса Классификация двигателей внутреннего сгорания
Классификация двигателей внутреннего сгорания Относительность движения
Относительность движения Методики (методы) измерений
Методики (методы) измерений Проводники и диэлектрики в электростатическом поле
Проводники и диэлектрики в электростатическом поле Теория автоматического управления. Типовые звенья
Теория автоматического управления. Типовые звенья Использование здоровьеформирующей технологии Ю.Г.Иванова на уроках физики
Использование здоровьеформирующей технологии Ю.Г.Иванова на уроках физики Тела, вещества, частицы
Тела, вещества, частицы Контактные методы экологического мониторинга
Контактные методы экологического мониторинга Биосенсоры
Биосенсоры Упругие колебания стержня с закрепленным концом
Упругие колебания стержня с закрепленным концом Где живет электричество? 8 класс
Где живет электричество? 8 класс Теоретическая механика
Теоретическая механика Давление
Давление Показатели надежности электроснабжения
Показатели надежности электроснабжения Трубки газоразрядные
Трубки газоразрядные Основные положения молекулярно-кинетической теории
Основные положения молекулярно-кинетической теории Жан Лерон Д' Аламбер. Трактат о динамике
Жан Лерон Д' Аламбер. Трактат о динамике