Теория групп и квантовая физика ХХ век

Принципы симметрии и теория групп
“Доисторические времена” (1927-1962):
элементарные частицы, атомы, молекулы, кристаллы
(классификация состояний, правила отбора, “скрытая” симметрия атома водорода, группы Лоренца, Пуанкаре и классификация частиц)‏
E. Wigner

“Новая эра” (1962 -1973):
Классификация адронов SU(3), SU(6), симметрия ароматов, кварки
Динамические симметрии квантовых систем
Спектр генерирующие алгебры
Когерентные состояния
M. Gell-Mann
A.O. Barut

“Новейшая история” (1973- …):
калибровочные поля
спонтанное нарушение симметрии
суперсимметричные модели
суперструны, d – branes and “Theory of Everything”

Теория групп и квантовая оптика?
Нелинейная оптика. Вырожденный параметрический генератор. (SU(1,1))‏
Сжатый свет
Квантовый хаос
Двух- и много- уровневые атомы
Cavity QED, micromaser
Диссипативные квантовые системы
Квантовые вычисления, декогеренция

Модельные гамильтонианы квантовой оптики и когерентные состояния

Coherent States on Lie Group G

John R. Klauder
Departments of Physics and Mathematics, University of Florida, Gainesville

Интеграл по траекториям в представлении КС

“Классические” уравнения движения

N-level atoms in Classical Fields. G = SU(N)‏

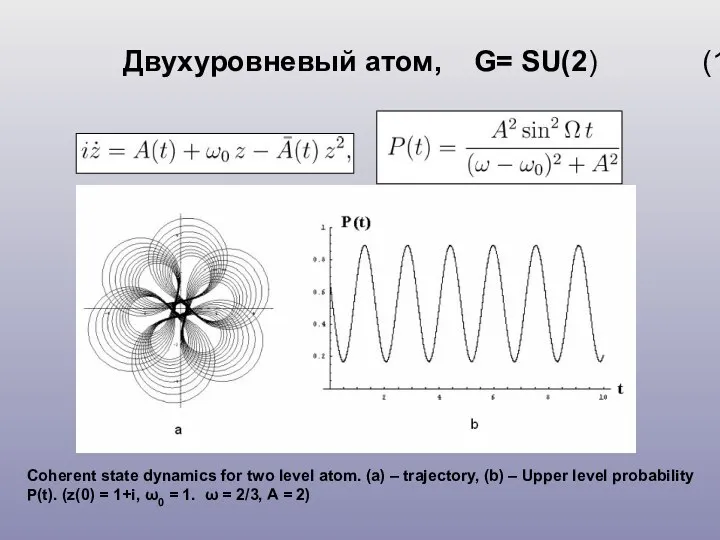
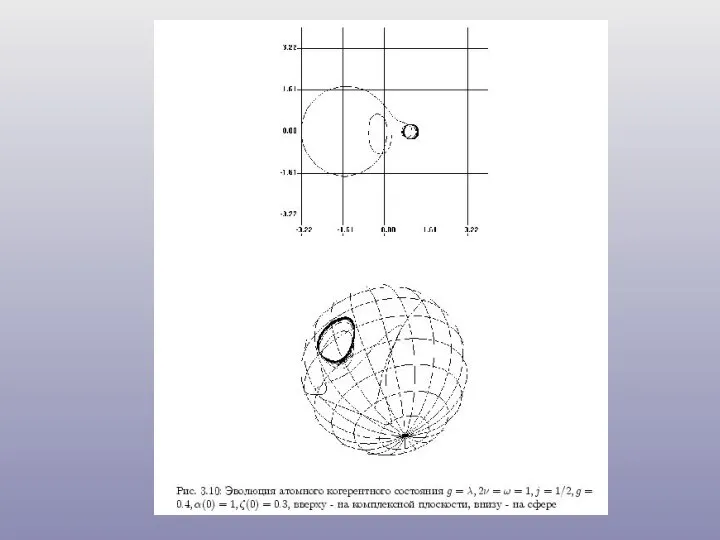
Двухуровневый атом, G= SU(2) (1)‏
Coherent state dynamics for two level atom. (a) – trajectory, (b) – Upper level probability P(t). (z(0) = 1+i, ω0 = 1. ω = 2/3, A = 2)‏

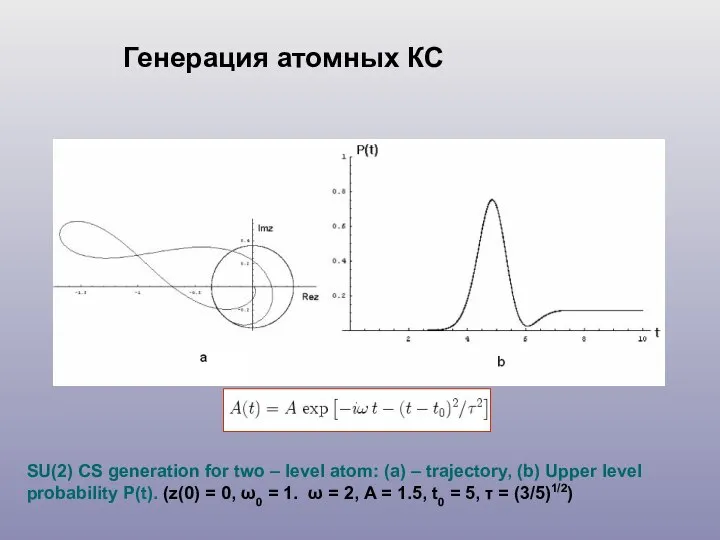
SU(2) CS generation for two – level atom: (a) – trajectory, (b) Upper level probability P(t). (z(0) = 0, ω0 = 1. ω = 2, A = 1.5, t0 = 5, τ = (3/5)1/2)‏
Генерация атомных КС

Трехуровневые атомы, G = SU(3)‏

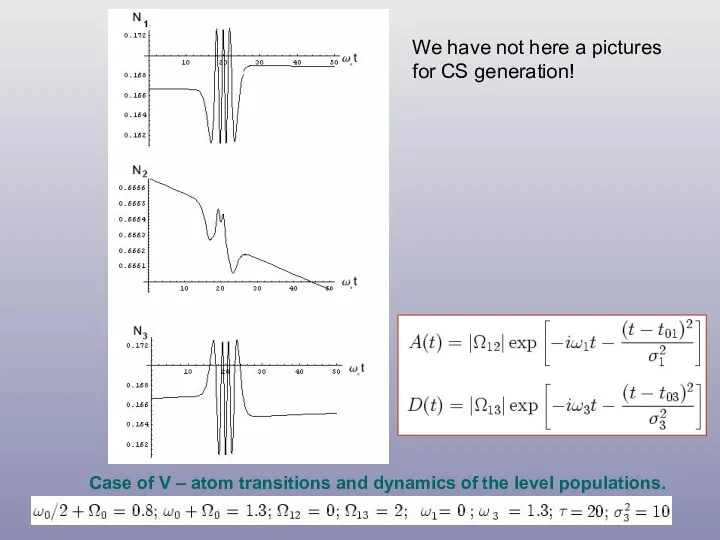
Case of V – atom transitions and dynamics of the level populations.
We have not here a pictures for CS generation!

Динамический хаос в квантовых системах

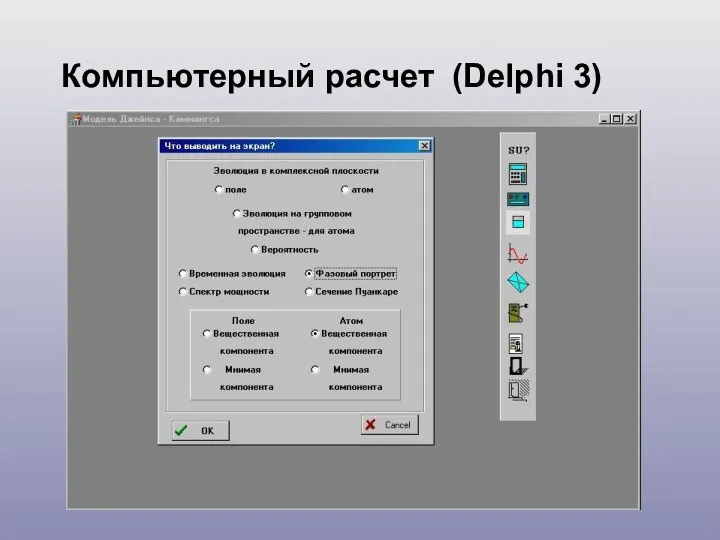
Компьютерный расчет (Delphi 3)‏

Операторные средние и квантовый хаос

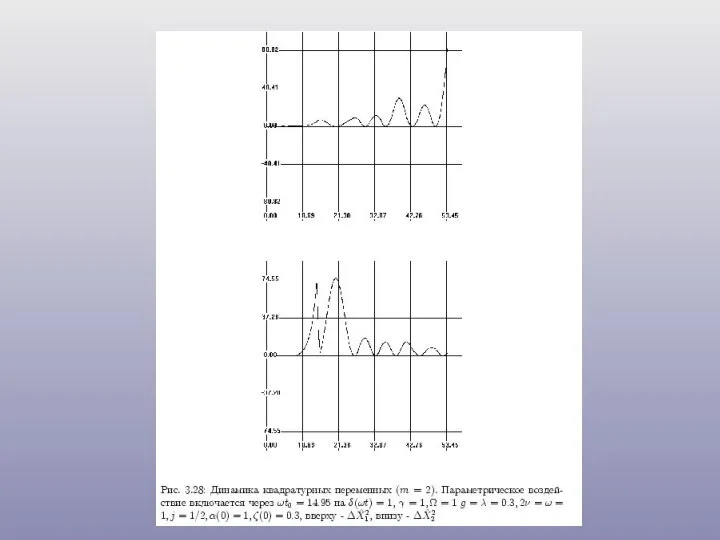
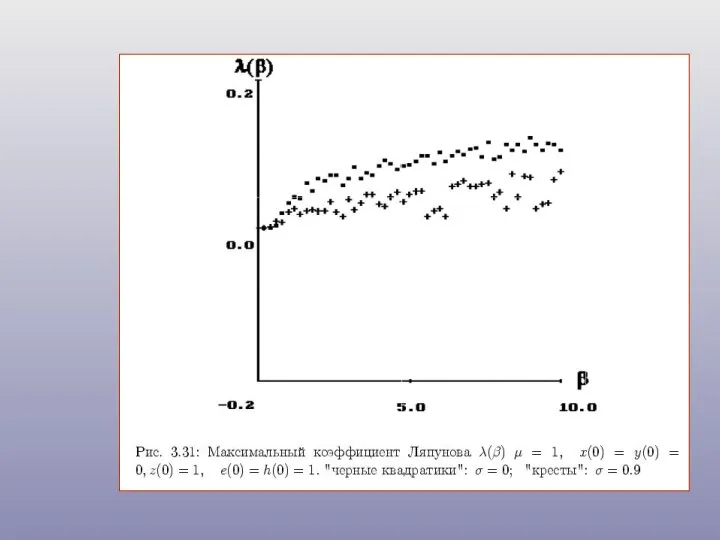
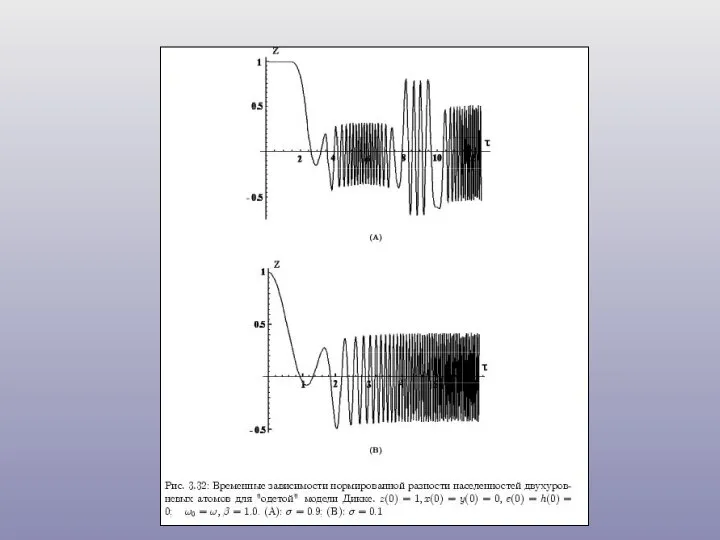
Обобщенная модель Дикке с затуханием, максимальный показатель Ляпунова и сжатие

Когерентная релаксация квантовых систем с конечным числом уровней

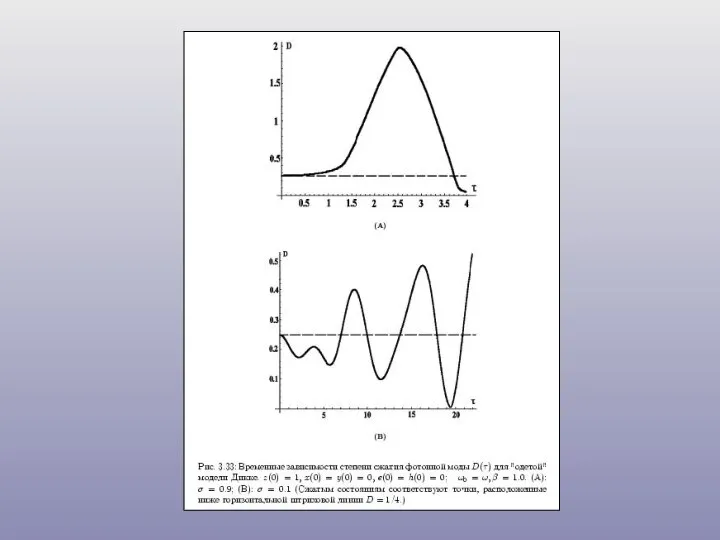
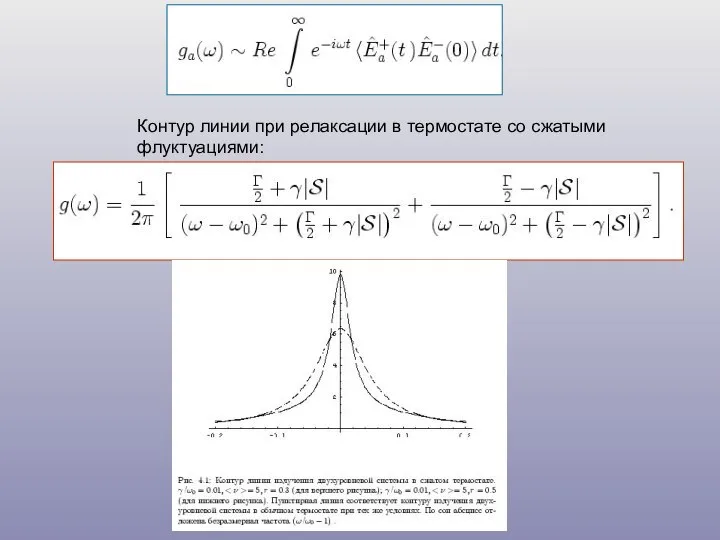
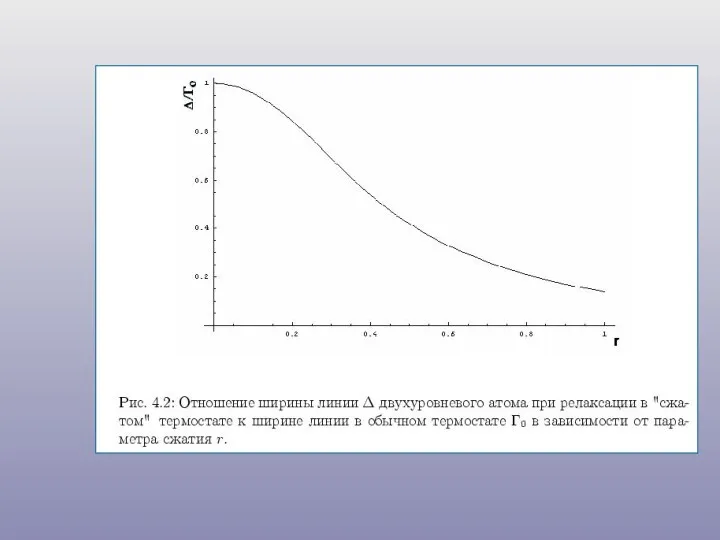
Контур линии при релаксации в термостате со сжатыми флуктуациями:

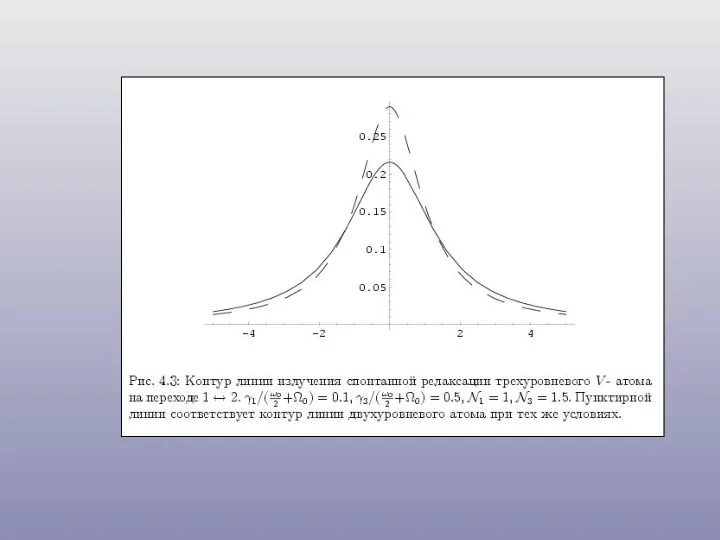
Трехуровневые атомы

Two level system in external stochastic fields
and Fokker – Planck Equation (FPE) Approach

FPE - Propagator for Atom in Stochastic Field
Weak Field. Perturbation theory
White noise
Kubo - Andersen processes
Markov’s dichotomic processes
“Exact Soluble” Model

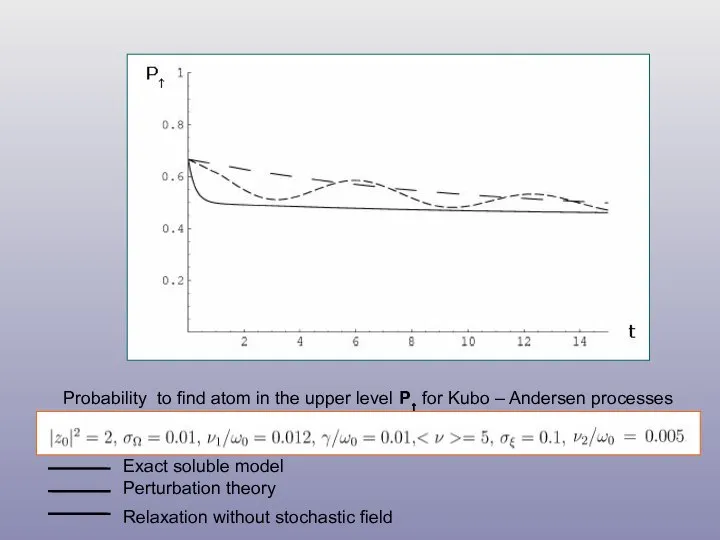
Probability to find atom in the upper level P↑ for Kubo – Andersen processes
Exact soluble model
Perturbation theory
Relaxation without stochastic field

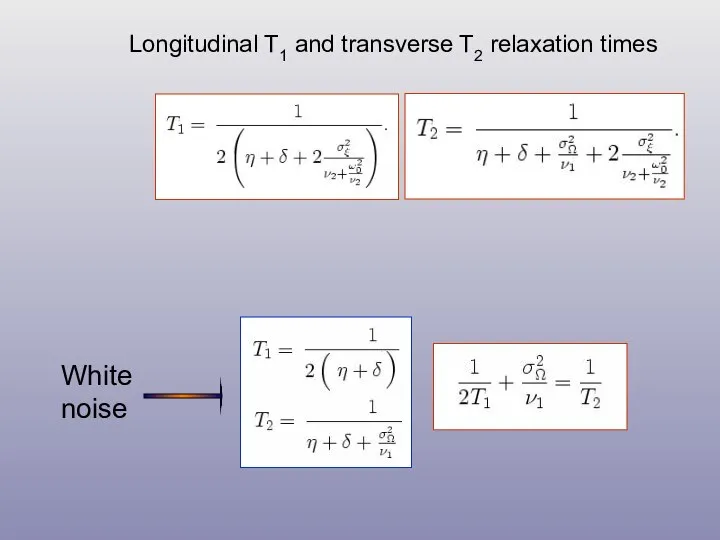
Longitudinal T1 and transverse T2 relaxation times
White noise

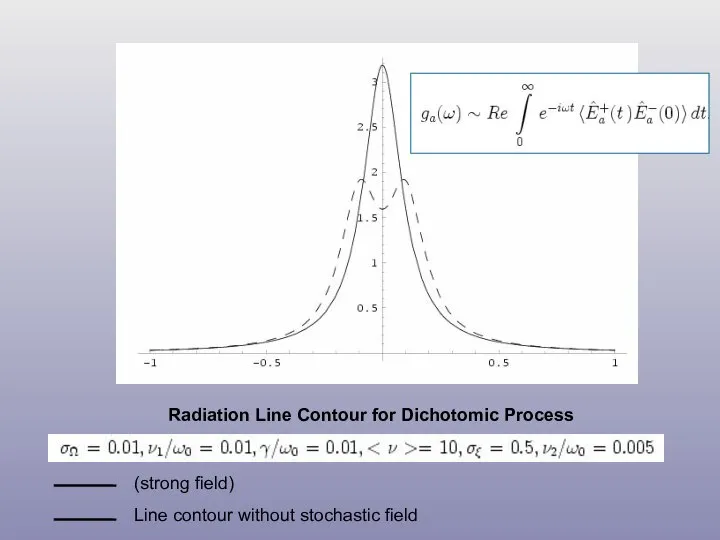
Radiation Line Contour for Dichotomic Process
(strong field)‏
Line contour without stochastic field

Dipole – dipole interacting atoms

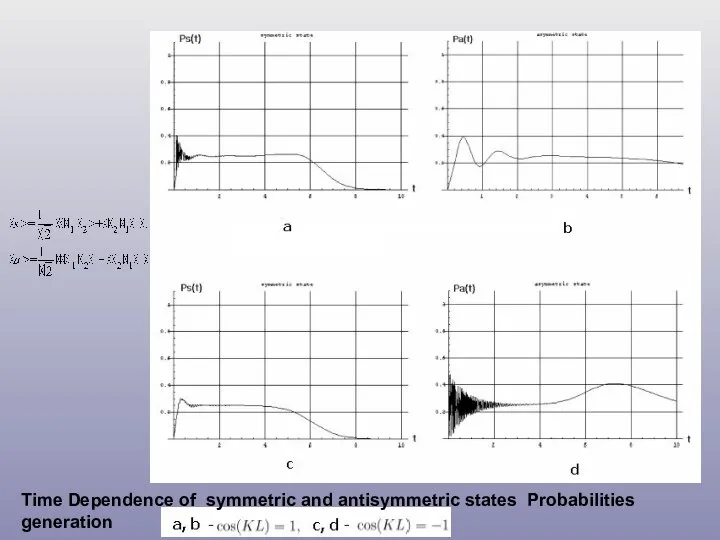
Time Dependence of symmetric and antisymmetric states Probabilities generation

Перспективы метода теории групп и когерентных состояний
Бесконечномерные обертывающие алгебры
Супералгебры и супергруппы
Атомные конденсаты
Квантовая теория информации
Квантовая инженерия
Квантовая томография
Квантовые игры
??? !!! …