Содержание
- 2. Колебания – это движение или процессы, которые точно или приблизительно повторяются через определенный промежуток времени.
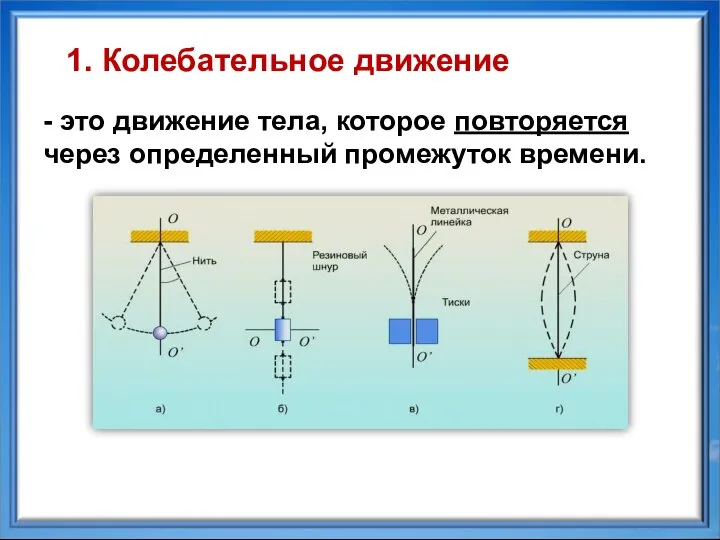
- 3. - это движение тела, которое повторяется через определенный промежуток времени. 1. Колебательное движение
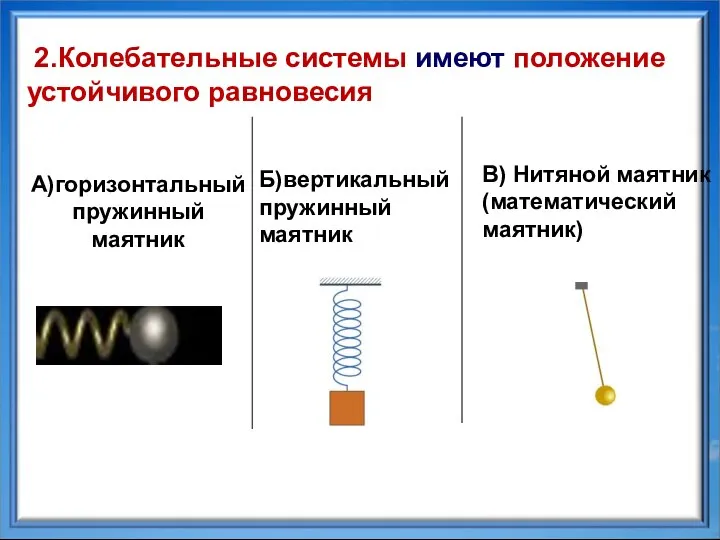
- 4. А)горизонтальный пружинный маятник Б)вертикальный пружинный маятник 2.Колебательные системы имеют положение устойчивого равновесия В) Нитяной маятник (математический
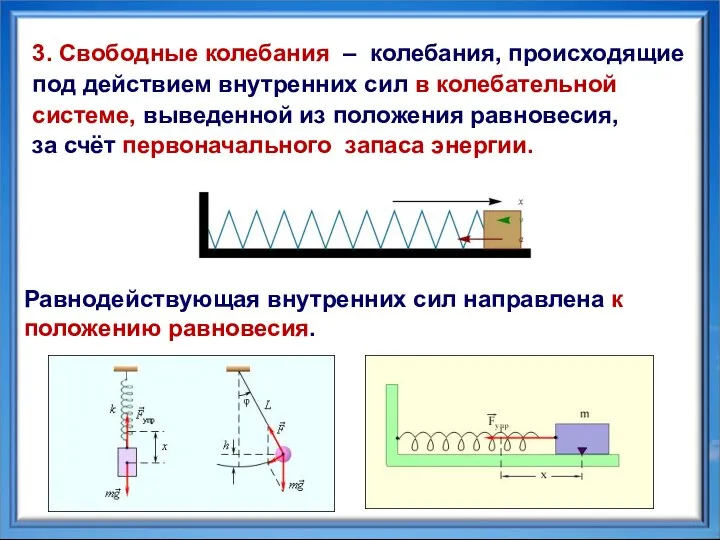
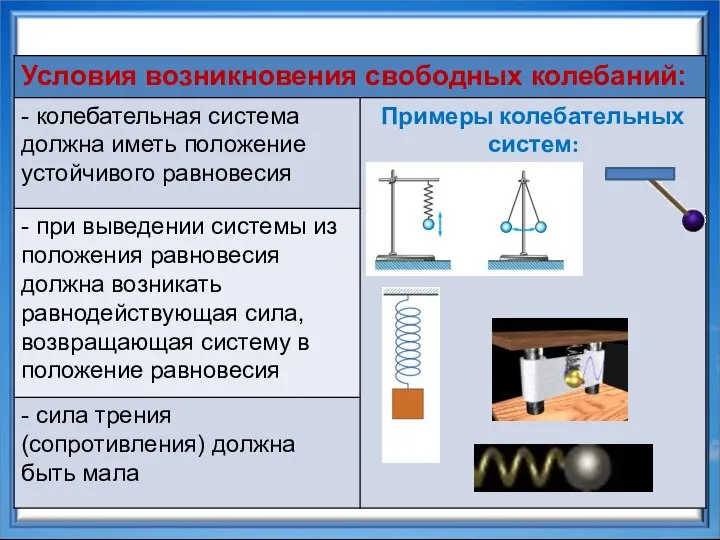
- 5. 3. Свободные колебания – колебания, происходящие под действием внутренних сил в колебательной системе, выведенной из положения
- 7. 4. Амплиnуда колебаний хm - модуль наибольшего смещения тела от положения равновесия. Определяется начальными условиями (энергией).
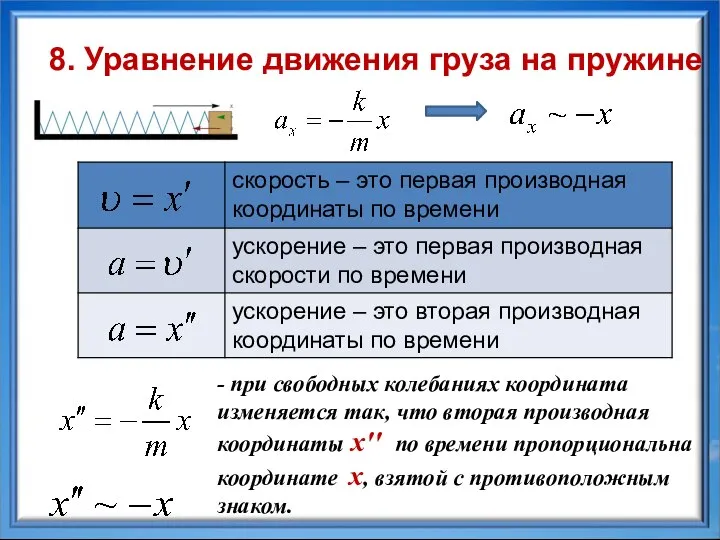
- 8. В проекциях на ОХ: Уравнение движения: По II закону Ньютона: Проекция ах ускорения тела прямо пропорциональна
- 9. - при свободных колебаниях координата изменяется так, что вторая производная координаты хꞌꞌ по времени пропорциональна координате
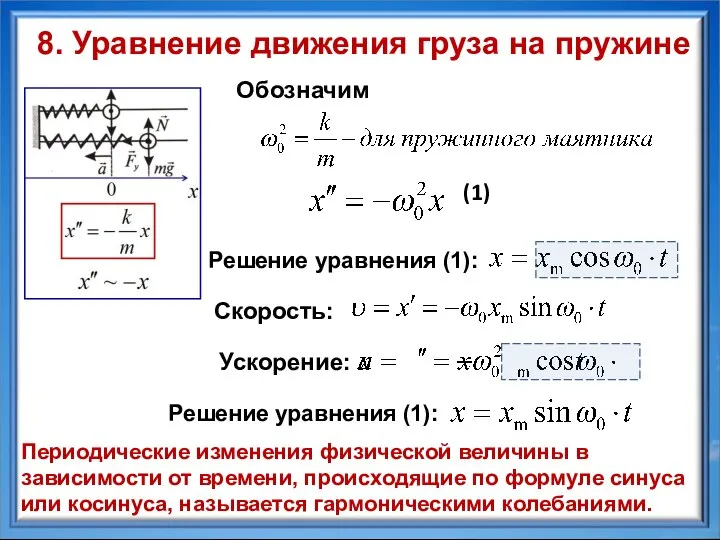
- 10. Решение уравнения (1): Периодические изменения физической величины в зависимости от времени, происходящие по формуле синуса или
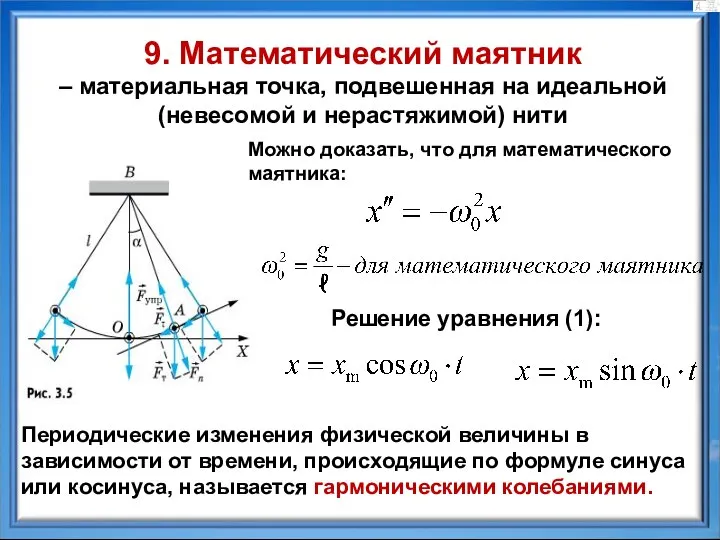
- 11. 9. Математический маятник – материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити Решение уравнения (1):
- 12. Через время Т при увеличении аргумента косинуса на ω0Т значение координаты повторяется. Наименьший период у косинуса
- 13. 11.Период колебаний груза на пружине Т 12.Период колебаний математического маятника Т
- 14. Фаза колебаний определяет значения координаты, скорости, ускорения, изменяющихся тоже по гармоническому закону. 13. Фаза колебаний φ
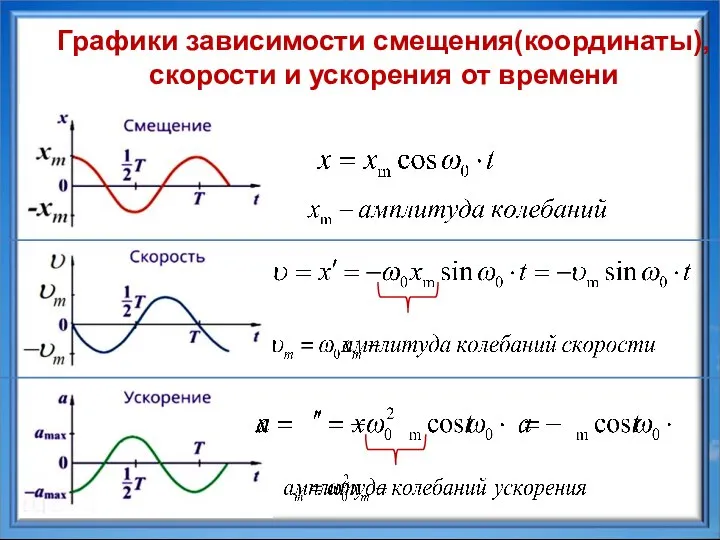
- 15. Графики зависимости смещения(координаты), скорости и ускорения от времени
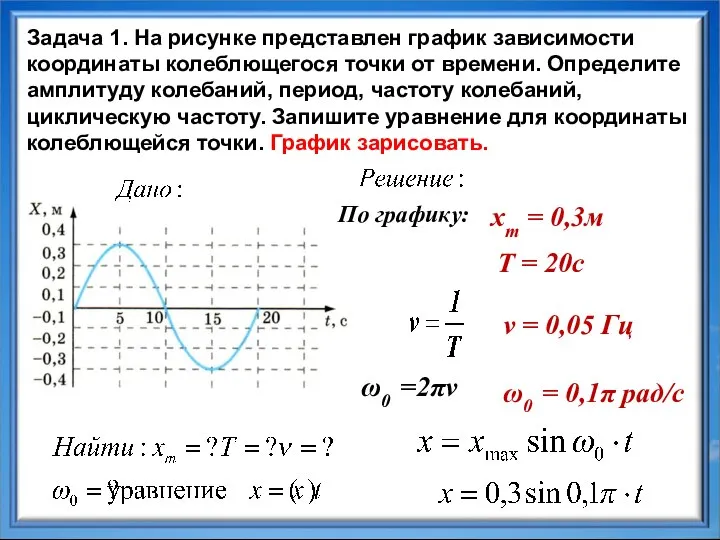
- 16. xm = 0,3м Задача 1. На рисунке представлен график зависимости координаты колеблющегося точки от времени. Определите
- 17. Задача 2. Материальная точка совершает гармонические колебания согласно уравнению в котором все величины заданы в единицах
- 19. Скачать презентацию







 Действие жидкости и газа на погружённое в них тело. Сила Архимеда
Действие жидкости и газа на погружённое в них тело. Сила Архимеда Равноуск. движение
Равноуск. движение Электронная абсорбционная спектроскопия
Электронная абсорбционная спектроскопия Основы электротехники. Основные понятия и законы
Основы электротехники. Основные понятия и законы Полимерные композиционные материалы – исходные компоненты и их свойства. Лекция 2
Полимерные композиционные материалы – исходные компоненты и их свойства. Лекция 2 Двигатели внутреннего сгорания
Двигатели внутреннего сгорания Силы упругости и трения
Силы упругости и трения Презентация на тему Поверхностное натяжение жидкостей
Презентация на тему Поверхностное натяжение жидкостей  Вимушені коливання. Резонанс (Лекція 4)
Вимушені коливання. Резонанс (Лекція 4) Виды излучения. Спектры. Спектральный анализ
Виды излучения. Спектры. Спектральный анализ Переходные процессы в ЭЦ
Переходные процессы в ЭЦ История создания и применение тепловых двигателей
История создания и применение тепловых двигателей Презентация на тему Фотоэффект
Презентация на тему Фотоэффект  Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Secret Portkey
Secret Portkey Велоподготовка для дальних поездок
Велоподготовка для дальних поездок Свечение ламп в магнитном поле, созданном катушкой индуктивности
Свечение ламп в магнитном поле, созданном катушкой индуктивности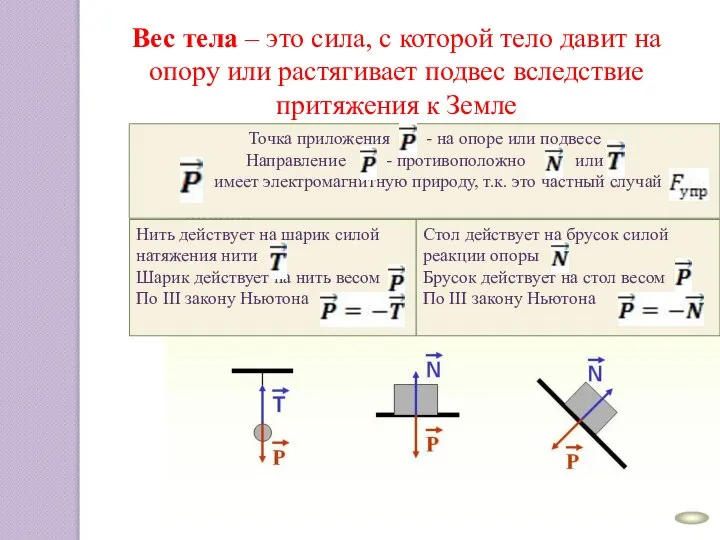 Вес тела
Вес тела Что такое физика
Что такое физика Спектры и спектральный анализ
Спектры и спектральный анализ Ионное испарение. Механизм распыления при ионном испарении. Катодное испарение: диодное, диодное со смещением и триодное
Ионное испарение. Механизм распыления при ионном испарении. Катодное испарение: диодное, диодное со смещением и триодное Презентация на тему Электромагнитное поле
Презентация на тему Электромагнитное поле  Момент силы относительно точки и оси. Теория пар сил. Приведение произвольной системы сил к заданному центру. Теорема Вариньона
Момент силы относительно точки и оси. Теория пар сил. Приведение произвольной системы сил к заданному центру. Теорема Вариньона Плазма и её свойства
Плазма и её свойства Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры
Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры Ремонт портальных мостов. Учебное пособие
Ремонт портальных мостов. Учебное пособие 4
4 Механические колебания, вибрация
Механические колебания, вибрация