Содержание
- 2. Понятие устойчивости Термин «устойчивость» используется в численных методах, механике, экономике, социологии, психологии. Во всех этих науках
- 3. Равновесие и устойчивость Шарик на рисунке находится в устойчивом равновесии в положении А - если немного
- 4. Устойчивость системы Система «шарик-горка» - нелинейная. Для неё • устойчивость - не свойство системы, а свойство
- 5. Устойчивость системы
- 6. Виды устойчивости Известно несколько определений устойчивости, которые отличаются некоторыми деталями. Если рассматривать только выход системы при
- 7. Виды устойчивости (1) Внутренняя или математическая устойчивость означает, что не только выход, но и все внутренние
- 8. Устойчивость «вход-выход» Обычно для инженеров в первую очередь важно, чтобы система не «пошла вразнос», то есть,
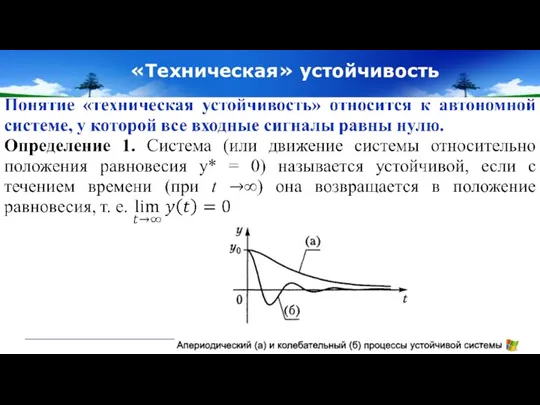
- 9. «Техническая» устойчивость
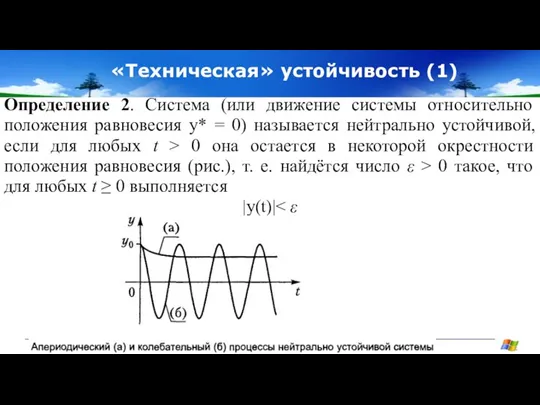
- 10. «Техническая» устойчивость (1) Определение 2. Система (или движение системы относительно положения равновесия у* = 0) называется
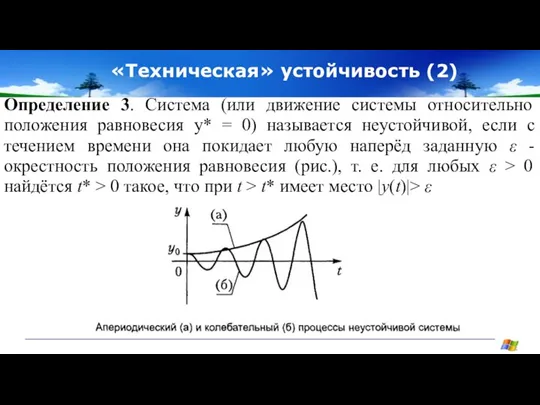
- 11. «Техническая» устойчивость (2) Определение 3. Система (или движение системы относительно положения равновесия у* = 0) называется
- 12. Внутренняя устойчивость Говоря о внутренней устойчивости, рассматривают не только выход, но и все переменные, описывающие состояние
- 13. Внутренняя устойчивость. Состояние системы Говоря о внутренней устойчивости, рассматривают не только выход, но и все переменные,
- 14. Фазовое пространство При рассмотрении устойчивости полезным оказалось введение некоторых наглядных геометрических понятий и представлений. Основным из
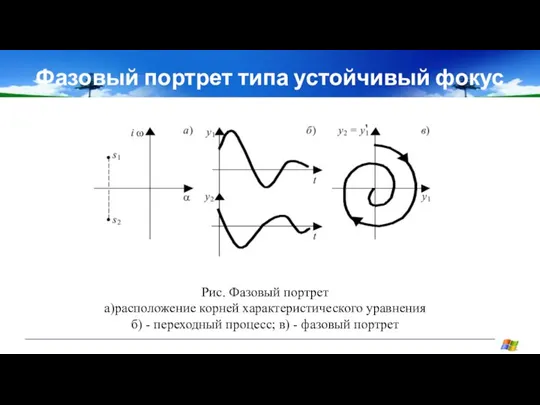
- 15. Фазовый портрет типа устойчивый фокус Рис. Фазовый портрет а)расположение корней характеристического уравнения б) - переходный процесс;
- 16. Устойчивость движения Движение называется невозмущённым, если оно получено в результате рассмотрения идеализированной системы. Движение с учётом
- 17. Малые возмущения Уточним, что понимается под малыми возмущениями. Любые возмущения можно разделить на два типа: импульсные
- 18. Малые возмущения (1)
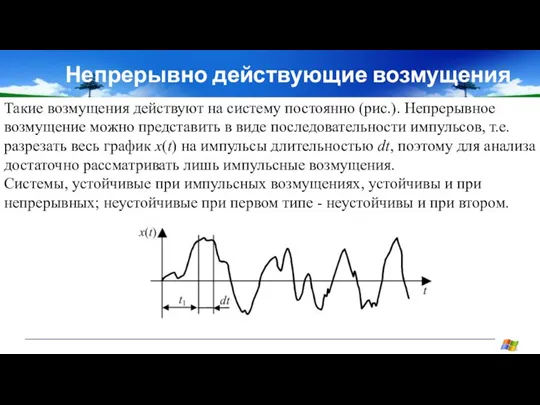
- 19. Непрерывно действующие возмущения Такие возмущения действуют на систему постоянно (рис.). Непрерывное возмущение можно представить в виде
- 20. ε-окрестность движения При анализе устойчивости вводится понятие ε-окрестности невозмущённого движения. С этой целью рассматривается траектория невозмущённого
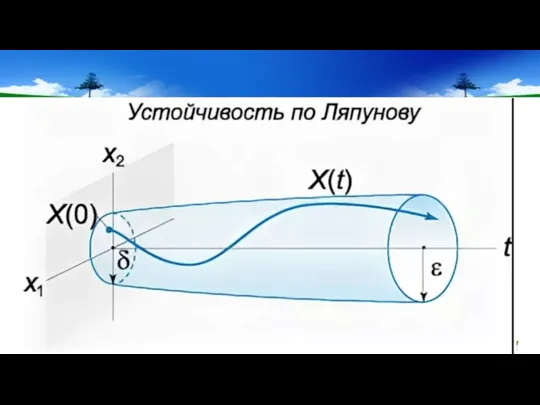
- 21. Определение устойчивости по Ляпунову Формальное определение внутренней устойчивости было введено в работах А.М. Ляпунова, поэтому такое
- 23. Устойчивость по Ляпунову Фактически это означает, что чем меньше начальное отклонение, тем меньше траектория движения отклоняется
- 24. Пример устойчивой системы Рассмотрим маятник на рисунке ниже (а), состоящий из подвешенного металлического стержня и шарика.
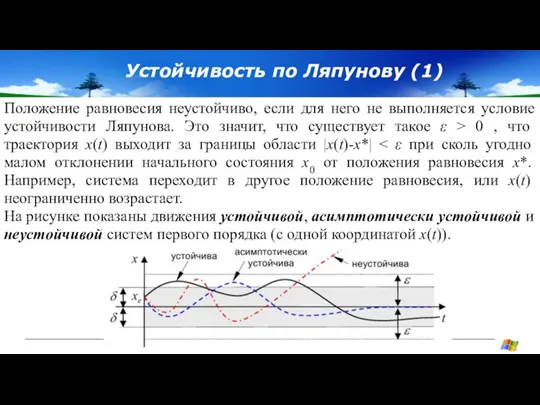
- 25. Устойчивость по Ляпунову (1) Положение равновесия неустойчиво, если для него не выполняется условие устойчивости Ляпунова. Это
- 26. Устойчивость по Ляпунову (2) Если вектор состояния содержит несколько переменных, для оценки разности векторов х0 -
- 27. Особенности устойчивости линейных систем Автономная линейная система может иметь единственное положение равновесия (в котором все сигналы
- 28. Условия устойчивости линейных систем Для того, чтобы получить условия устойчивости, рассмотрим уравнение движения линейной системы, на
- 29. Условия устойчивости линейных систем (1) Поскольку устойчивость линейной системы определяют корни полинома Δ(s) - знаменателя передаточной
- 30. Нейтрально устойчивая система Предположим, что один из корней полинома Δ(s) равен нулю (скажем, α1 = 0),
- 31. Нейтрально устойчивая система (1) Допустим, что характеристический полином имеет пару чисто мнимых корней: α1 = jω
- 32. Движение в пространстве состояний Рассмотрим систему (рис.) с m входами (u1,u2,...,um), r выходами (y1,y2,..., yr) и
- 33. Модель системы в пространстве состояний В общем случае, рассматриваемая система может быть определена следующей векторно-матричной формой
- 34. Устойчивость внутренних процессов Теперь посмотрим, как определить внутреннюю устойчивость линейной системы, то есть, устойчивость внутренних процессов.
- 35. Устойчивость внутренних процессов . Сначала для простоты будем считать, что матрица А имеет вид Тогда уравнение
- 36. Устойчивость внутренних процессов (1) Если все корни характеристического полинома устойчивы (имеют отрицательные вещественные части, расположены в
- 37. Устойчивость линеаризованных систем Устойчивость нелинейной системы можно во многих случаях оценивать с помощью линеаризованной системы. Для
- 38. Устойчивость экономики в форме модели Самуэльсона — Хикса Характеристическое уравнение (полином) модели Самуэльсона—Хикса имеет следующий вид
- 39. Устойчивость экономики в форме модели Самуэльсона — Хикса (1) Если дискриминант отрицателен: , то уравнение имеет
- 41. Скачать презентацию































 Общий порядок построения эпюр Qx и Мх
Общий порядок построения эпюр Qx и Мх Измерение скоростей молекул газа. (Урок 48)
Измерение скоростей молекул газа. (Урок 48) Механика. Молекулярная физика
Механика. Молекулярная физика Неисправность источники электрической энергии, способы проверки и ремонта
Неисправность источники электрической энергии, способы проверки и ремонта Виды энергии
Виды энергии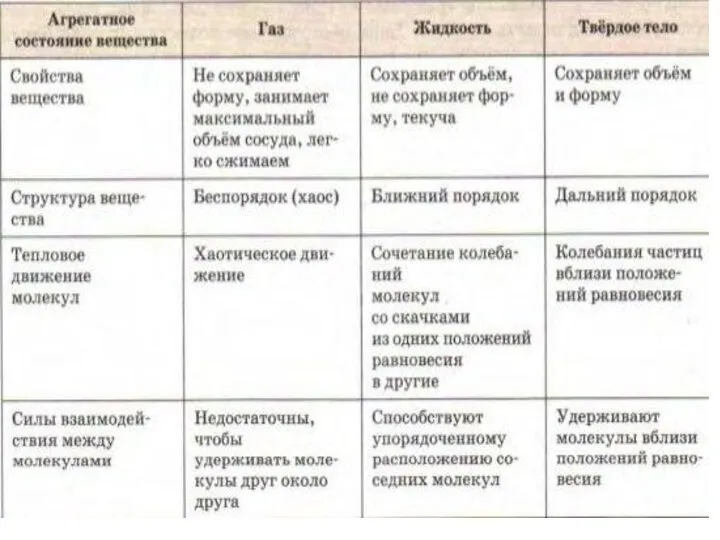 Свойства жидкостей
Свойства жидкостей Трение. Сила трения. Коэффициент трения скольжения
Трение. Сила трения. Коэффициент трения скольжения Тепловые двигатели
Тепловые двигатели Дифракция света
Дифракция света Волновые свойства света
Волновые свойства света Закон сохранения момента импульса
Закон сохранения момента импульса Теплотехнические измерения. Практическое занятие
Теплотехнические измерения. Практическое занятие Электропривод. Проектирование электроприводов
Электропривод. Проектирование электроприводов Оптика. Законы отражения
Оптика. Законы отражения Интерференция света
Интерференция света Физико-химические методы анализа
Физико-химические методы анализа Презентация на тему Перспективы развития физики
Презентация на тему Перспективы развития физики  Скорость движения
Скорость движения Погрузочно-транспортные машины типа пд и пт
Погрузочно-транспортные машины типа пд и пт Шалаев Хиггс
Шалаев Хиггс Задачи. Мощность
Задачи. Мощность Отраслевая олимпиада ПАО РусГидро по физике Энергия образования для школьников 7-11 классов
Отраслевая олимпиада ПАО РусГидро по физике Энергия образования для школьников 7-11 классов Условия плавания тел
Условия плавания тел Презентация на тему Закон Ома для участка цепи
Презентация на тему Закон Ома для участка цепи  Лазерные технологии
Лазерные технологии Гармонические колебания. Амплитуда, период и частота колебательного движения
Гармонические колебания. Амплитуда, период и частота колебательного движения Оптика. Законы преломления
Оптика. Законы преломления Понятие о машине и механизме. Урок Технология
Понятие о машине и механизме. Урок Технология