Слайд 2Уравнение теплопроводности
Этот раздел посвящен элементам теории теплопроводности. Основы этой теории были заложены

французским математиком Фурье (1768-1830) в первой четверти XIX века.
Плотностью потока теплоты называется вектор j, совпадающий по направлению с направлением распространения теплоты и численно равный количеству теплоты, проходящему в одну секунду через площадку в один квадратный метр, перпендикулярную к направлению потока теплоты.
Слайд 3Уравнение теплопроводности
Пусть имеется неограниченная среда, в которой возникает поток теплоты в направлении,

параллельном оси X.
Выделим мысленно в среде цилиндр с образующими, параллельными оси X, и рассмотрим бесконечно малый участок такого цилиндра АВ длины dx
Слайд 13Стационарное распределение температуры в плоскопараллельной пластинке
Допустим, что имеется бесконечная пластинка толщины l,

поверхности которой поддерживаются при постоянных температурах Т1 и Т2-
Требуется найти распределение температуры T внутри такой пластинки. Примем за ось X прямую, перпендикулярную к пластинке. Начало координат поместим на плоскости 1, ограничивающей пластинку.
Слайд 14Стационарное распределение температуры в плоскопараллельной пластинке

Слайд 15Стационарное распределение температуры в плоскопараллельной пластинке

Слайд 16Стационарное распределение температуры в плоскопараллельной пластинке

Слайд 17Стационарное распределение температуры в плоскопараллельной пластинке

Слайд 18Распределение температуры между двумя концентрическими сферами

Слайд 19Распределение температуры между двумя концентрическими сферами

Слайд 20Стационарное распределение температуры между двумя цилиндрами.

Слайд 22Течение вязкой жидкости
Пусть между двумя параллельными твердыми пластинами с расстоянием h между

ними находится жидкость с вязкостью η.
Пусть нижняя пластина покоится, а верхняя движется со скоростью u0.
Слайд 33Уравнение диффузии и его применение

Слайд 34Уравнение диффузии и его применение
В качестве примера применения этого уравнения, рассмотрим следующую

задачу.
По трубке длиной l слева направо текут пары ртути, а навстречу им идет диффузионный поток откачиваемого газа (воздуха)
Слайд 35Уравнение диффузии и его применение
Найдем скорость прокачки ртути, при которой концентрация молекул

воздуха будет меняться на длине трубки от n1 до n0
Слайд 36Уравнение диффузии и его применение
Молярный вес воздуха равен 29 г/моль, для ртути

он составляет 200 г/моль, т.е. на порядок больше. Поэтому в струе паров ртути происходит передача импульса диффундирующим молекулам воздуха.
Слайд 37Уравнение диффузии и его применение

Слайд 38Уравнение диффузии и его применение

Слайд 39Уравнение диффузии и его применение

Слайд 40Уравнение диффузии и его применение
Этот процесс имеет практическое применение в технике высокого

вакуума.
В 1901 г. русский физик П.Н. Лебедев проводил эксперименты с использованием вакуумных установок. В его установках для достижения высокого вакуума использовался модифицированный ртутный поршневой насос, где остаточные молекулы газа захватывались парами ртути и откачивались вместе с ними. Идея использовать пары ртути для удаления остаточного газа привлекла внимание многих ученых.







































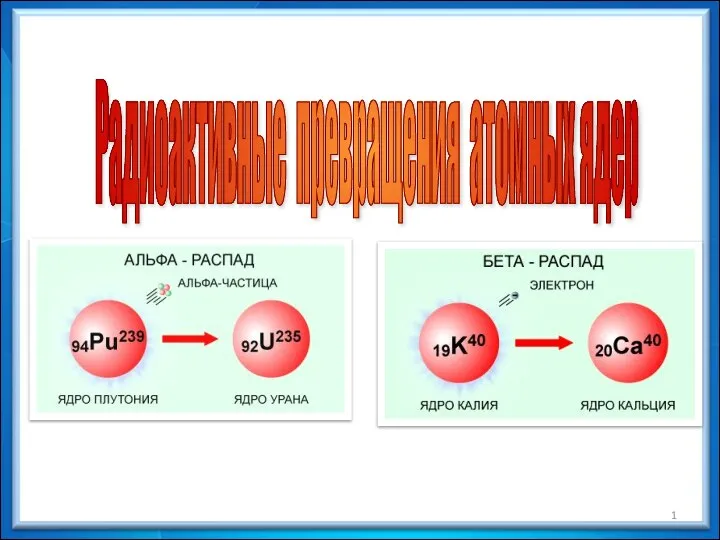 Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Микромир элементарных частиц
Микромир элементарных частиц 840842
840842 prezentaciya_chto_izuchaet_fizika
prezentaciya_chto_izuchaet_fizika Использование энергии Солнца на Земле
Использование энергии Солнца на Земле Звук и его характеристики
Звук и его характеристики Электротехника и электроника. Трёхфазные электрические цепи синусоидального тока
Электротехника и электроника. Трёхфазные электрические цепи синусоидального тока 1 нче сорау Фотоэффект вакытында нәрсә күзәтелә? А. Атомнарн
1 нче сорау Фотоэффект вакытында нәрсә күзәтелә? А. Атомнарн Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Строение атомов
Строение атомов Реактивная сила
Реактивная сила Кинематика. Занятие 4
Кинематика. Занятие 4 Презентация на тему КПД тепловых двигателей (8 класс)
Презентация на тему КПД тепловых двигателей (8 класс)  Подшипники насосов и компрессоров
Подшипники насосов и компрессоров Презентация по физике "Оптические иллюзии или Обман зрения" -
Презентация по физике "Оптические иллюзии или Обман зрения" -  Путь. Перемещение. Определение координаты движущегося тела. 9 класс
Путь. Перемещение. Определение координаты движущегося тела. 9 класс Электрические цепи переменного тока
Электрические цепи переменного тока Вес тела. Невесомость
Вес тела. Невесомость Окружающие нас тела называются физическими телами. Строение вещества. Молекула
Окружающие нас тела называются физическими телами. Строение вещества. Молекула Презентация на тему Радиация: проблемы и перспективы
Презентация на тему Радиация: проблемы и перспективы  Шпоночное соединение
Шпоночное соединение Пропеллеры в мультикоптерах
Пропеллеры в мультикоптерах Закон сохранения механической энергии
Закон сохранения механической энергии Новости физики и химии
Новости физики и химии Получение, использование, история исследования, диапазон, длина волны
Получение, использование, история исследования, диапазон, длина волны Лампы ДРЛ (Дуговая Ртутная лампа)
Лампы ДРЛ (Дуговая Ртутная лампа) Фазовые переходы (лекция 4)
Фазовые переходы (лекция 4) Работа и мощность электрического тока
Работа и мощность электрического тока