Содержание
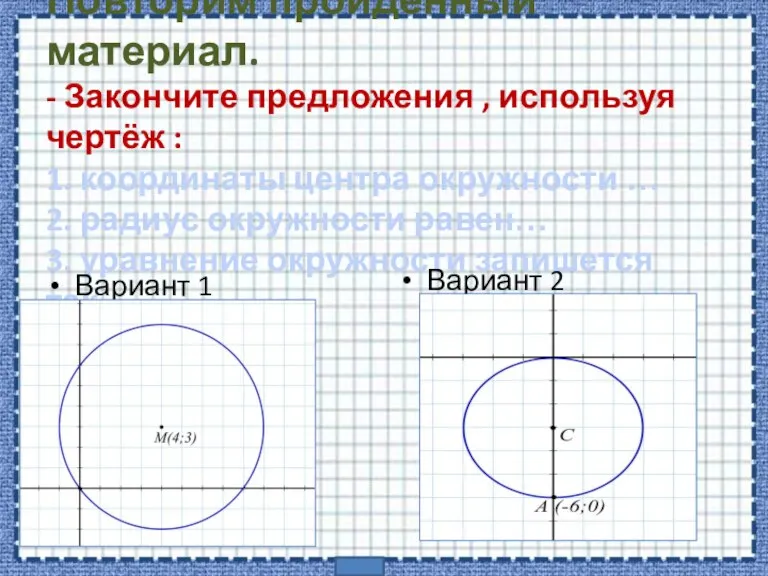
- 2. Повторим пройденный материал. - Закончите предложения , используя чертёж : 1. координаты центра окружности … 2.
- 3. Подсказка…
- 4. Решение задач у доски. Даны две точки А (1;-2) и В (2;4) а) Найдите координаты вектора
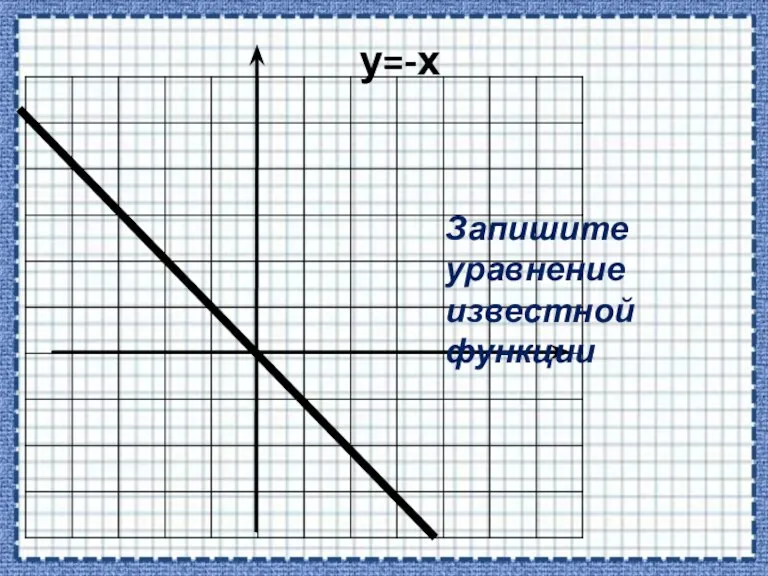
- 5. у=-х Запишите уравнение известной функции
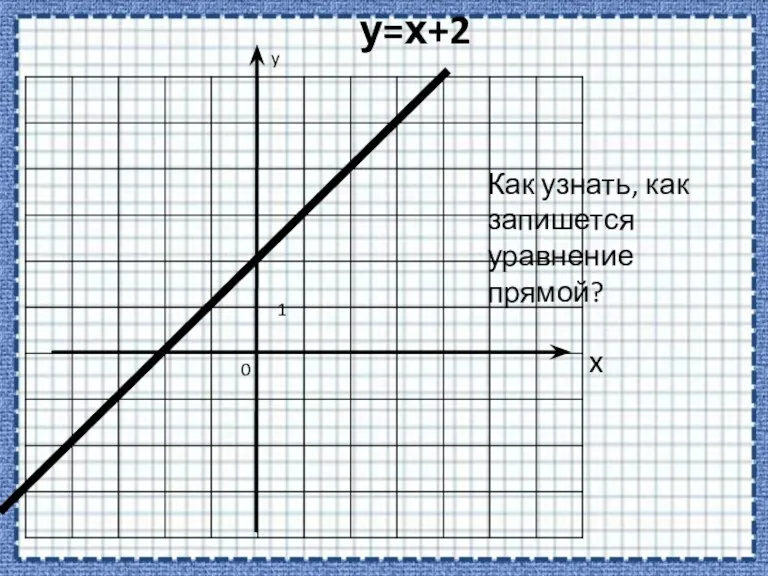
- 6. у=х+2 Как узнать, как запишется уравнение прямой? y x 0 1
- 7. Любая прямая в координатах x, y имеет уравнение вида: ax + by + c = 0,
- 8. Решим полученную систему: Выразим коэффициенты a и b через коэффициент c: В уравнении a + c
- 9. Итак, мы получили новые значения a и b: a = -c, b = -2c. Теперь в
- 10. РАБОТАЕМ С УЧЕБНИКОМ: 1. П. 95 учебника геометрии 7-9. № 972 (а) – совместно № 972
- 11. Другой способ составления уравнения прямой Подумайте , как написать уравнение прямой , проходящей через две данные
- 12. ИТАК , уравнение прямой
- 13. Диктант Принадлежит ? Что является графиком? А центр ?
- 14. Проверь себя 1.АВ=5; 2.М – центр окружности, М(3;-5); 3.принадлежит 4.прямая 5.х=3 – параллельна ОУ, У=-1 –
- 16. Скачать презентацию










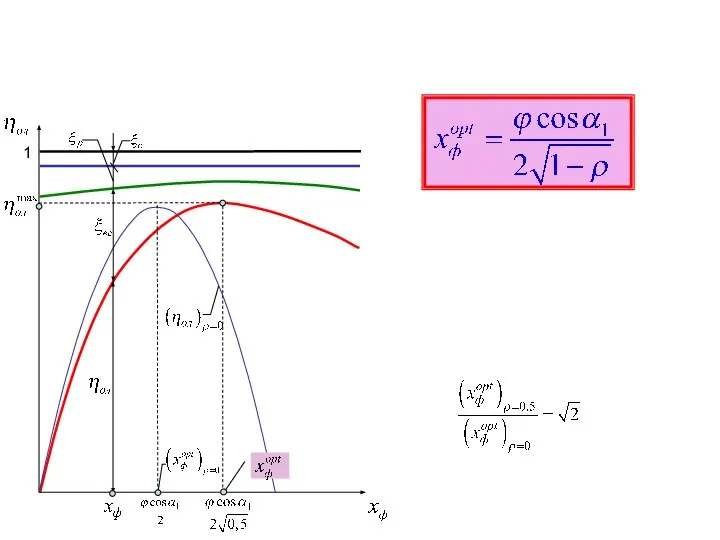 Оптимальный располагаемый теплоперепад ступени
Оптимальный располагаемый теплоперепад ступени Уравнение х2=a
Уравнение х2=a Интересная математика
Интересная математика Графики элементарных функций. Повторение
Графики элементарных функций. Повторение Действия с числами, записанными в стандартном виде
Действия с числами, записанными в стандартном виде Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Квадратный корень из степени
Квадратный корень из степени Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Решение квадратных уравнений
Решение квадратных уравнений Касательная и ее свойства
Касательная и ее свойства Цилиндр. Урок математики
Цилиндр. Урок математики Прямо-пропорциональные величины
Прямо-пропорциональные величины Измерение углов
Измерение углов Логарифмические неравенства
Логарифмические неравенства Презентация по теории вероятностей. На тему:”Описательная статистика”.
Презентация по теории вероятностей. На тему:”Описательная статистика”. Презентация на тему Одночлены. Арифметические операции над одночленами
Презентация на тему Одночлены. Арифметические операции над одночленами  Свойства функций
Свойства функций Криволинейные интегралы
Криволинейные интегралы Многоугольники. Урок № 1
Многоугольники. Урок № 1 Элементы математической логики
Элементы математической логики Признаки равенства треугольников
Признаки равенства треугольников Презентация по математике "Двоичная арифметика. Сложение Вычитание Умножение" -
Презентация по математике "Двоичная арифметика. Сложение Вычитание Умножение" -  Округление десятичных дробей
Округление десятичных дробей Корреляционный анализ в Exel
Корреляционный анализ в Exel Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем
Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем Конкурс А ну-ка, математики!
Конкурс А ну-ка, математики! Решение неравенств с одной переменной
Решение неравенств с одной переменной Линейное уравнение с одной переменной
Линейное уравнение с одной переменной