Слайд 2
Характер теплового движения молекул Лекция 6
Вероятность того, что в данном направлении будет
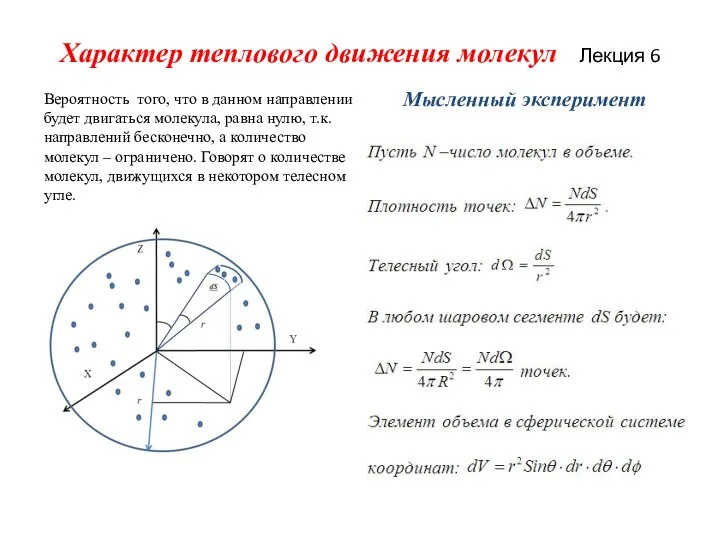
двигаться молекула, равна нулю, т.к. направлений бесконечно, а количество молекул – ограничено. Говорят о количестве молекул, движущихся в некотором телесном угле.
Мысленный эксперимент
Слайд 3
Элемент объема в сферической системе координат: Лекция 6
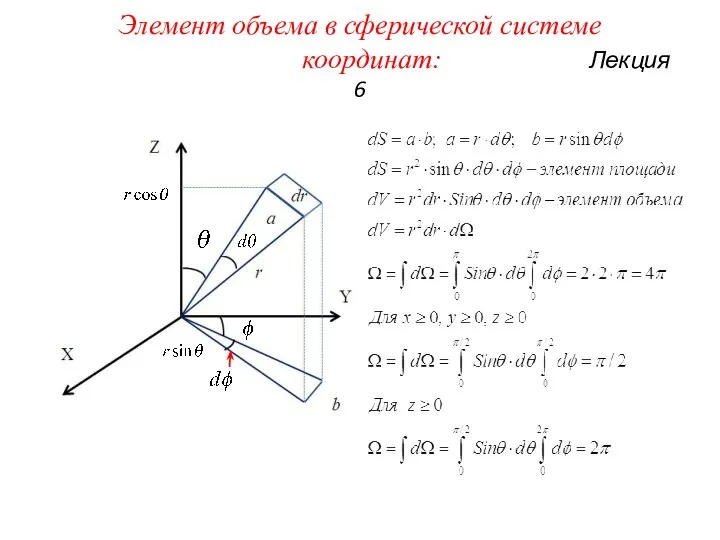
Слайд 4
Число ударов молекул о стенку Лекция 6
Считаем количество ударов молекул об

элемент поверхности стенки сосуда dS за время dt.
1. Выделяем N – молекул со скоростями: от v до v+dv. Обозначим их число: dNv.
2. Выделяем из dNv молекулы внутри . Обозначим их число: .
3. За время dt из этих молекул долетят только те, которые находятся в косом цилиндре с основанием dS и высотой .
Доля таких молекул:
Число таких молекул: , или
Слайд 5
Число ударов молекул о стенку Лекция 6
Полное число молекул за dt ударившихся

в dS будет:
n – плотность числа частиц
Число молекул, ударившихся о единичную площадку за единицу времени:
Слайд 6
Давление Лекция 6
Давление определяется:
Стенка получает импульс:
А давление на этот элемент:
Изменение
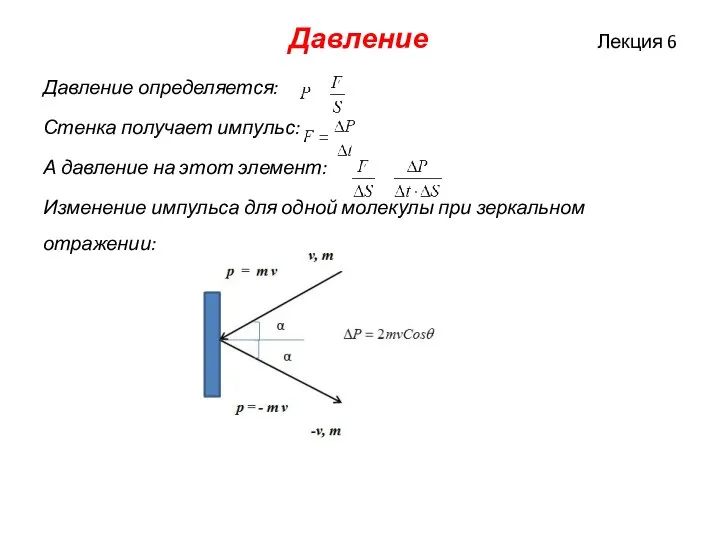
импульса для одной молекулы при зеркальном отражении:
Слайд 7Давление Лекция 6
Количество молекул, падающих на и имеющих скорости от v до

v+dv равно:
Тогда суммарный импульс будет:
Интегрируем по углам:
Слайд 8Давление Лекция 6
Тогда:
Получим выражение для давления:
Все молекулы одинаковые по массе:
- средняя кинетическая

энергия поступательного движения.
Слайд 9Пример
Есть 4 молекулы со скоростями: vi = 1,2,3,4.
Найти:

Слайд 10
Средняя энергия молекул Лекция 6
Мы получили:
Откуда:
Основное уравнение молекулярно-кинетической теории
-

усредненный микропараметр
T - макропараметр
Слайд 11
Средняя энергия молекул Лекция 6
Получаем скорость:
Вследствие эквивалентности направлений:
Поэтому,
Т.е.,

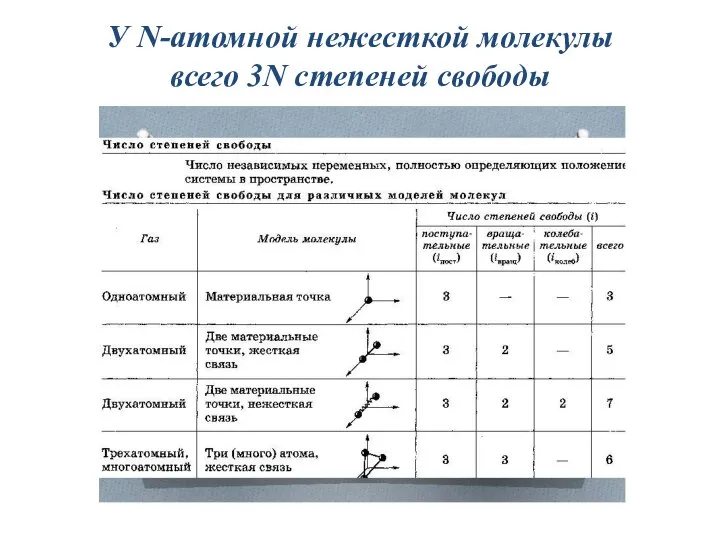
Слайд 12Степени свободы системы Лекция 6
Сложные молекулы могут вращаться и колебаться.
«Числом степеней свободы
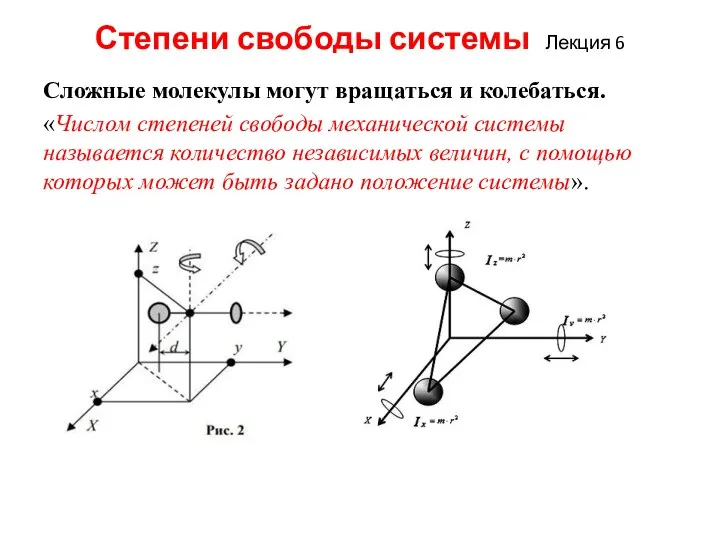
механической системы называется количество независимых величин, с помощью которых может быть задано положение системы».
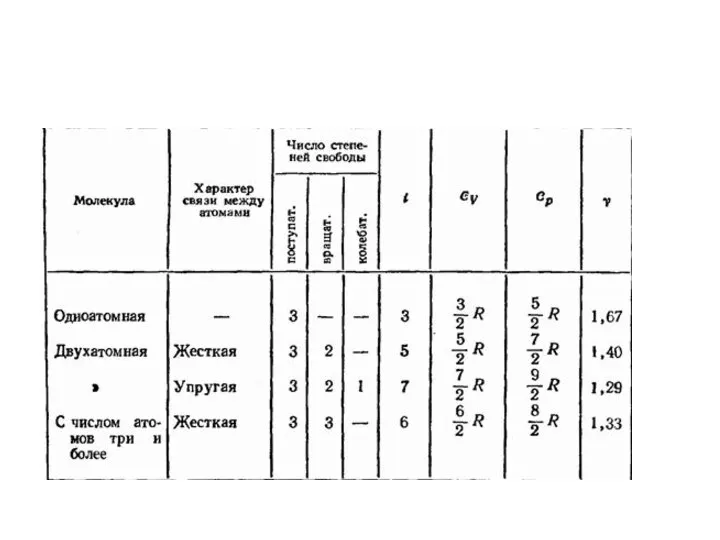
Слайд 13Закон равнораспределения энергии по степеням свободы Лекция 6
На каждую степень свободы приходится

kT/2 энергии.
Т.е. средняя энергия молекулы равна:
Где - полное число степеней свободы
Почему у колебательной степени энергия в 2 раза больше?
Слайд 14Идеальный газ Лекция 6
Внутренняя энергия 1 моля идеального газа равна
С другой

стороны:
Отсюда:
Слайд 15У N-атомной нежесткой молекулы
всего 3N степеней свободы














 Система охлаждения компьютера
Система охлаждения компьютера Строение атома
Строение атома Презентация на тему Кабинет физики
Презентация на тему Кабинет физики  Импульс тела. Закон сохранения
Импульс тела. Закон сохранения Управление вертолетом. Основные моменты
Управление вертолетом. Основные моменты Светостабилизаторы
Светостабилизаторы Что изучает физика (урок 1)
Что изучает физика (урок 1) Инерция (7 класс)
Инерция (7 класс) Изучение характера движения тела, скатывающегося по наклонной плоскости
Изучение характера движения тела, скатывающегося по наклонной плоскости Принцип Гюйгенса. Дифракция механических волн. Волновое движение
Принцип Гюйгенса. Дифракция механических волн. Волновое движение Рентгеновские трубки (РТ). Классификация. Обозначение. Основные характеристики. (Лекция 4)
Рентгеновские трубки (РТ). Классификация. Обозначение. Основные характеристики. (Лекция 4) Электромагниты
Электромагниты Плазма и ионизирующие излучения в атомной и космической промышленности. Тема 1
Плазма и ионизирующие излучения в атомной и космической промышленности. Тема 1 mehanicheskie_kolebaniya
mehanicheskie_kolebaniya agregatnye_sostoyania_8_kl
agregatnye_sostoyania_8_kl Скорость выполнения работы. Формула работы
Скорость выполнения работы. Формула работы Самоіндукція. Індуктивність. Енергія магнітного поля
Самоіндукція. Індуктивність. Енергія магнітного поля Качественные задачи
Качественные задачи Физика в игрушках
Физика в игрушках Презентация по физике "Зависимость силы тока от напряжения. Сопротивление проводника" -
Презентация по физике "Зависимость силы тока от напряжения. Сопротивление проводника" -  Ламинарное течение жидкости через тонкие цилиндрические трубки (задачи)
Ламинарное течение жидкости через тонкие цилиндрические трубки (задачи) 0013de4b-e4a557ac
0013de4b-e4a557ac Решение задач Агрегатные состояния
Решение задач Агрегатные состояния Механические явления. 7 класс
Механические явления. 7 класс Лекция 1. Цели и задачи дисциплины
Лекция 1. Цели и задачи дисциплины Статические ИО тока. Лекции 10
Статические ИО тока. Лекции 10 Определение видов дефектов в автоматических устройствах горного оборудования с последующим их устранением
Определение видов дефектов в автоматических устройствах горного оборудования с последующим их устранением Расчёт режимов разомкнутых сетей
Расчёт режимов разомкнутых сетей