Содержание
- 2. Исторический пример Несмотря на то, что при каждом акте радиоактивного распада только небольшая часть массы исходного
- 3. В 1905 г. Э. фон Швейдлер, используя имеющиеся к тому времени экспериментальные данные, ввел статистические понятия
- 4. Т. о., вероятность того, что данный радионуклид проживет временной интервал t, дается выражением exp(–λt). Если в
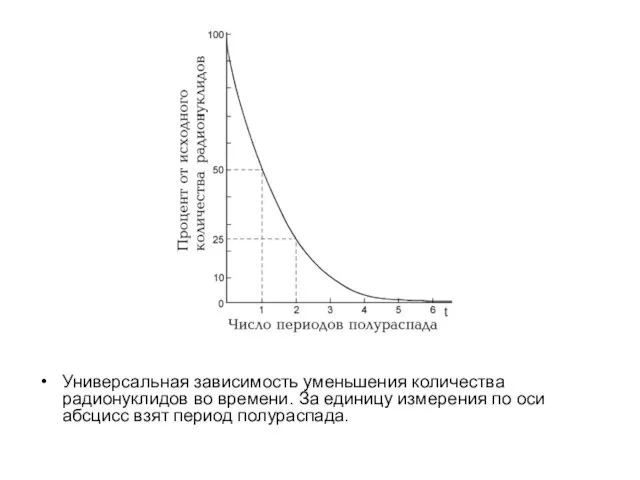
- 5. Универсальная зависимость уменьшения количества радионуклидов во времени. За единицу измерения по оси абсцисс взят период полураспада.
- 6. Скорость распада, т. е. уменьшение числа радионуклидов в единицу времени –dN/dt, согласно (*), пропорциональна числу имеющихся
- 7. Активность определяется следующим соотношением: A = λ·N = –dN/dt; A = A0·e–λt, A (t = 0)
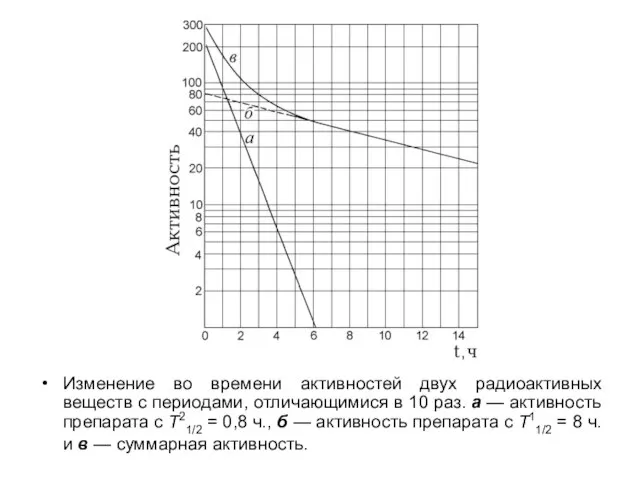
- 8. Изменение во времени активностей двух радиоактивных веществ с периодами, отличающимися в 10 раз. а — активность
- 9. Более сложный и более важный в экологическом отношении случай, когда у нас второй радионуклид образуется при
- 10. Пусть λ2 > λ1. Через интервал времени t, λ2·t > 3, т. е. через ~4 периода
- 11. а — активность дочерней фракции, образующейся из материнской, T1/2 = 0,8 ч.; б — активность материнских
- 12. Особый интерес для радиоэкологии представляет случай λ2 >> λ1 — вековое равновесие (Secular Equilibrium). За время,
- 13. В начале XX в. наибольшей удельной активностью обладал 226Ra (T1/2 = ~1600 лет; 1 г 226Ra
- 14. д
- 15. Несмотря на то, что для характеристики количества радионуклидов или плотностей загрязнений в радиоэкологии используется активность, часто
- 16. Рассмотрим пример. В результате Чернобыльской аварии загрязненность некоторых территорий составила ~1,5·106 Бк·м-2 по радионуклиду 137Cs (T1/2
- 17. Флуктуации На практике в радиоэкологии, когда нет сильного загрязнения, часто возникает следующая ситуация. Допустим, нам нужно
- 18. Промежуточный вывод 1. Для количественного определения загрязнения окружающей среды радионуклидами или их содержания в каком-то объекте
- 19. 2. Что такое Радиоактивность. Термин «радиоактивность» был введен М. Кюри для обозначения спонтанного испускания ионизирующих, проникающих
- 20. 3. Стабильные и нестабильные ядра. Трудности возникают и при попытке дать определения терминам «стабильные нуклиды» и
- 21. 4. Сколько химических элементов естественного происхождения находится в окружающей нас природной среде. Самые тяжелые — свинец
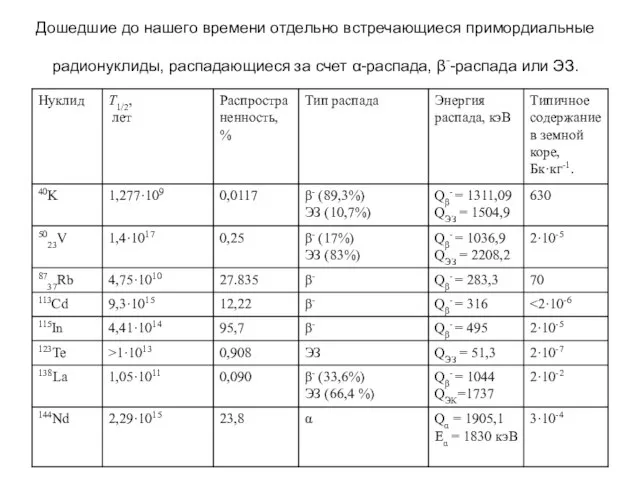
- 22. Дошедшие до нашего времени отдельно встречающиеся примордиальные радионуклиды, распадающиеся за счет α-распада, β--распада или ЭЗ.
- 23. 7·10-8
- 24. Дочерние продукты распада 232Th, 235U и 238U независимо от их периода полураспада постоянно присутствуют в окружающей
- 26. Скачать презентацию
Слайд 2Исторический пример
Несмотря на то, что при каждом акте радиоактивного распада только небольшая
Исторический пример
Несмотря на то, что при каждом акте радиоактивного распада только небольшая

1 г радия, находящийся в замкнутом объеме в равновесии с продуктами своего распада, выделяет в час около 670 Дж тепловой энергии. Иными словами, 1 г такого препарата каждые двое суток выделяет ~3,2·104 Дж энергии, т. е. столько, сколько высвобождается при сгорании ~1 г каменного угля.
В радии не наблюдается никаких химических изменений и кажется, что этот процесс может продолжаться сколь угодно долго. Способность радия и продуктов его распада непрерывно выделять энергию свидетельствовала о том, что само явление радиоактивности связано с выделением значительного количества энергии.
Слайд 3В 1905 г. Э. фон Швейдлер, используя имеющиеся к тому времени экспериментальные
В 1905 г. Э. фон Швейдлер, используя имеющиеся к тому времени экспериментальные

Для достаточно малых временных интервалов эта вероятность пропорциональна только интервалу — λ·Δt.
Коэффициент пропорциональности λ получил название постоянной распада и является характерной величиной для каждого радионуклида.
Вероятность того, что данный радионуклид "проживет" в течение интервала времени Δt равна 1 – λ·Δt, а в течение двух таких интервалов, согласно правилу умножения вероятностей, равна (1 – λ·Δt)2.
Вероятность того, что радионуклид проживет промежуток времени t = n·Δt, равна (1 – λt/n)n. Конечно, это выражение справедливо только для бесконечно малых промежутков времени Δt.
Предел такого выражения при n, стремящемся к бесконечности, хорошо известен из курса математики
lim(1+ x/n)n = ex.
n→∞
Слайд 4Т. о., вероятность того, что данный радионуклид проживет временной интервал t, дается
Т. о., вероятность того, что данный радионуклид проживет временной интервал t, дается

Если в рассматриваемом образце в начале содержалось N0 радионуклидов, то по истечении времени t из первоначального их количества останется
N = N0·e-λt. (*)
Это математическое выражение закона радиоактивного распада, а λ имеет простой смысл: это доля атомов, испытывающих превращения в единицу времени.
Длина отрезка времени должна быть при этом такой, что уменьшение исходного числа радионуклидов за этот промежуток времени должно быть малым по сравнению с исходным их числом N0. Константа распада имеет размерность, обратную времени, а показатель у экспоненты всегда безразмерная величина.
Во всевозможных таблицах радионуклидов приводится, как правило, не величина λ, а период полураспада T1/2. За это время исходное количество радионуклидов N0 уменьшается в два раза
T1/2 = ln2/λ = 0,693/λ.
Значения периодов полураспада для разных радионуклидов находятся в чрезвычайно широких пределах от ~10-7 с до ~1020 лет. Эти значения можно рассматривать как паспортные характеристики радионуклидов, которые неизменны, по крайней мере, за время существования Галактики.
Слайд 5Универсальная зависимость уменьшения количества радионуклидов во времени. За единицу измерения по оси
Универсальная зависимость уменьшения количества радионуклидов во времени. За единицу измерения по оси
Слайд 6Скорость распада, т. е. уменьшение числа радионуклидов в единицу времени –dN/dt, согласно
Скорость распада, т. е. уменьшение числа радионуклидов в единицу времени –dN/dt, согласно

–dN/dt = λ·N. (**)
Какие следствия для радиоэкологии следуют из вышесказанного? Если в окружающую среду в результате аварии попали короткоживущие радионуклиды, например с T1/2 < 1 часа, то маловероятно, чтобы за счет естественных процессов они загрязнили значительную территорию. Более того, через день об их присутствии можно забыть. Чем меньше T1/2, тем более локализовано воздействие радионуклидов на окружающую среду. Однако для населения, находящегося рядом с источником выброса радионуклидов, опасность может быть значительной, особенно в тех случаях, когда радионуклиды находятся в воздушной среде.
Интенсивность излучений, конечно, определяется числом атомов N, но в не меньшей мере она определяется постоянной распада (см. выражение (**)) и типом нуклидов.
Чтобы было удобно сопоставлять воздействия радионуклидов, в радиоэкологии количество радионуклидов того или иного типа выражают не в граммах или молях, а через скорость распада этого количества радионуклидов. Эта величина получила название активность — A. Именно она, с учетом типа радионуклидов, определяет радиационную обстановку в интересующем нас месте.
В научной литературе активность так же, как и массовое число нуклида, обозначают буквой A. Мы будем использовать для них разные шрифты.
Слайд 7Активность определяется следующим соотношением:
A = λ·N = –dN/dt; A = A0·e–λt,
Активность определяется следующим соотношением:
A = λ·N = –dN/dt; A = A0·e–λt,

В радиоэкологии, как правило, приходится иметь дело со смесью радионуклидов. Формально говоря, активность смеси радионуклидов всегда равна сумме активностей отдельных компонент. Однако нужно помнить, что такая характеристика, как суммарная активность, имеет мало смысла при оценках воздействия, так как воздействие определяется не только активностью, но и энергией и схемой распада. В природе не существует двух типов радионуклидов, которые при равной активности оказывали бы равное воздействие. Различия в воздействии двух разных радионуклидов с одинаковой активностью на живую ткань могут составлять от процентов до десятков тысяч раз.
Основные закономерности, связанные с кинетикой распада, проследим на примере рассмотрения смеси только двух типов радионуклидов. Наблюдаемая в этом случае активность равна:
A = A1 + A2 = λ1·N1 + λ2·N2.
Пусть периоды полураспада радионуклидов: T11/2 = 8 ч. и T21/2 = 0,8 ч.. Со временем вклад в суммарную активность более короткоживущего компонента уменьшается и ее зависимость от времени в полулогарифмическом масштабе, переходит в прямую, соответствующую долгоживущему компоненту.
Слайд 8Изменение во времени активностей двух радиоактивных веществ с периодами, отличающимися в 10
Изменение во времени активностей двух радиоактивных веществ с периодами, отличающимися в 10
Слайд 9Более сложный и более важный в экологическом отношении случай, когда у нас
Более сложный и более важный в экологическом отношении случай, когда у нас

Рассмотрим распад материнского вещества и предположим, что в начале измерений количество материнского радионуклида равно N10, а дочернего нет, т. е. N20 = 0.
Образование дочерних ядер происходит с той же скоростью, что и распад материнских — λ1·N1, а распад их происходит со скоростью – λ2·N2. По аналогии с (**), мы можем записать dN2/dt = λ1·N1 – λ2·N2, или, несколько видоизменив, имеем
dN2/dt + λ2·N2 – λ1·N10·(exp(-λ1t) = 0
Решение такого линейного дифференциального уравнения первого порядка хорошо известно и c учетом того, что N20 = 0, записывается в виде
N2 = λ1·N10 [(exp(-λ1t) - (exp(-λ2t)]/(λ2 – λ1) (****)
Основной интерес представляет зависимость количества радионуклидов (или их активности) от соотношения между постоянными распада. Значения постоянных распада λi определяют величины активности в любой из моментов времени при заданном N10.
При анализе распада и накопления радионуклидов обычно выделяют области подвижного равновесия (Transient Equilibrium), когда λ2 > λ1, и отсутствия равновесия, когда λ1 > λ2.
=
Слайд 10Пусть λ2 > λ1. Через интервал времени t, λ2·t > 3, т.
Пусть λ2 > λ1. Через интервал времени t, λ2·t > 3, т.

N2 = N10 ·(exp(-λ1t)·λ1/( λ2 – λ1).
Так как N1 = N10·(exp(-λ1t), то мы получаем:
N1/N2 = (λ2 – λ1)/λ1. ()
Отношение же активностей Ai = λi·Ni этих радионуклидов записывается в виде
A1/A2 = (λ2 – λ1)/λ2, ()
т. е. отношения количеств различных радионуклидов в окружающей среде в общем случае не равно отношению их активностей.
Кинетику распада в случае подвижного равновесия удобно проследить с помощью зависимостей активностей от времени, представленных на рис., где периоды полураспада взяты из предыдущего примера.
Слайд 11а — активность дочерней фракции, образующейся из материнской, T1/2 = 0,8 ч.;
а — активность дочерней фракции, образующейся из материнской, T1/2 = 0,8 ч.;
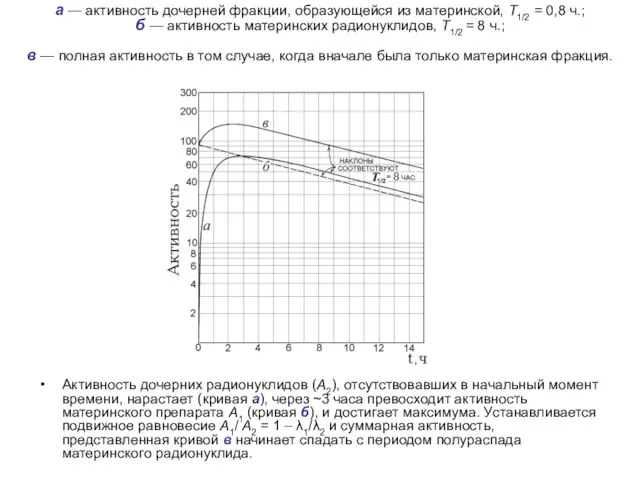
Активность дочерних радионуклидов (A2), отсутствовавших в начальный момент времени, нарастает (кривая а), через ~3 часа превосходит активность материнского препарата A1 (кривая б), и достигает максимума. Устанавливается подвижное равновесие A1/ A2 = 1 – λ1/λ2 и суммарная активность, представленная кривой в начинает спадать с периодом полураспада материнского радионуклида.
Слайд 12Особый интерес для радиоэкологии представляет случай λ2 >> λ1 — вековое равновесие
Особый интерес для радиоэкологии представляет случай λ2 >> λ1 — вековое равновесие

N1/N2 = λ2/ λ1 и A1 = A2 . ()
Такая ситуация справедлива для радиоактивных семейств 238U, 235U и 232Th, определяющих радиоактивность окружающей нас среды. Здесь мы имеем дело с цепочкой из более, чем 10 последовательных распадов. С анализом превращений во всей цепочке или в отдельных ее звеньях приходится сталкиваться при рассмотрении многих задач, связанных с поведением тяжелых естественных радионуклидов в биосфере.
В радиоэкологии хорошо известна и ситуация, когда λ1 > λ2. Это 241Pu, имеющий λ1 = 2,2·10-9 с-1, и распадающийся путем β-распада в более опасный радионуклид 241Am (λ2 = 7,35·10-11 с-1), распадающийся путем α-распада.
Разветвленный распад, т. е. материнский радионуклид может превратиться в разные дочерние. Пусть радионуклид Х распадается путем α-распада с постоянной распада λα в нуклид Б и путем β-распада с постоянной распада λβ в нуклид В. В этом случае количество атомов NX вещества Х уменьшается со скоростью (λα + λβ)·NX, а вещество Б образуется со скоростью λα·NX. Вещество Х, конечно, характеризуется только одним периодом полураспада T1/2 = 0,693/(λα + λβ), а определенно сказать, в какой нуклид превратится после распада радионуклид Х, нельзя.
Слайд 13В начале XX в. наибольшей удельной активностью обладал 226Ra (T1/2 = ~1600
В начале XX в. наибольшей удельной активностью обладал 226Ra (T1/2 = ~1600

0,693·2,664·1021/(1600·3,16·107 с) = 3,657·1010 распадов/с.
Период полураспада 226Ra на протяжении нескольких десятилетий постоянно уточнялся. Поэтому численное значение активности 1 г 226Ra также изменялось, что представляло определенные неудобства. Чтобы избежать этого, было принято, что 1 кюри ≡ 3,7·1010 распадов/с.
В миллионах кюри (МКи) измерялись выбросы при самых крупных радиационных авариях или взрывах атомных бомб. Активность источников, используемых для облучения экосистем или их частей при радиоэкологических исследованиях, измеряли тысячами кюри (кКи). Для исследования миграции веществ в биологических объектах использовали микрокюри (мкКи) необходимых для этого радионуклидов, а при анализе содержания радионуклидов в воде приходилось иметь дело с активностями, кратными 10-12 Ки на литр.
В 1960 г. на XI Генеральной конференции по мерам и весам было принято решение о полном переходе к Международной системе единиц СИ, официальной единицей активности стал беккерель (Бк), который рекомендуется использовать в настоящее время
1 Бк = 1 распад/с = 2,73·10-11 Ки.
В радиоэкологии для записей активностей и доз используют десятичные приставки.
Слайд 15Несмотря на то, что для характеристики количества радионуклидов или плотностей загрязнений в
Несмотря на то, что для характеристики количества радионуклидов или плотностей загрязнений в

Получим выражение для веса 1 Бк любого радионуклида.
По определению 1 Бк это есть 1 распад в секунду, т. е.
1 Бк = –dN/dt = λ·N = (0,693/T1/2)·N .
Активность 1 Бк всегда обусловлена N = 1/λ атомами и 1 Бк вещества, состоящего из радионуклидов с массовым числом А и периодом полураспада T1/2, весит m1 Бк
m1 Бк = (T1/2/0,693)·(A/6,02·1023) = 0,24·10-23 T1/2· A, грамм (*****).
Слайд 16Рассмотрим пример.
В результате Чернобыльской аварии загрязненность некоторых территорий составила ~1,5·106 Бк·м-2
Рассмотрим пример.
В результате Чернобыльской аварии загрязненность некоторых территорий составила ~1,5·106 Бк·м-2

σs ~(1,5·1012 с-1·км-2)·(137г)·(9,54·108 с)/0,693 ·6,02·1023 = 0,46 г·км-2.
Трудно ожидать, чтобы в реальных условиях из атмосферы вещество «вымывалось» так равномерно, чтобы в пределах каждого квадратного километра плотность его была бы постоянной, даже если само вещество хорошо диспергированно. В пределах каждого квадратного километра пробы, взятые в разных местах с площадок размером ~100 см2, как правило будут показывать значительные различия в плотности загрязнений. «Пятнистость» загрязнения территории радионуклидами очень четко проявилась при анализе последствий аварии на ЧАЭС.
Слайд 17Флуктуации
На практике в радиоэкологии, когда нет сильного загрязнения, часто возникает следующая ситуация.
Флуктуации
На практике в радиоэкологии, когда нет сильного загрязнения, часто возникает следующая ситуация.

Допустим, нам нужно откалибровать прибор и для этого определить содержание 137Cs в некотором стандартном образце активностью 1,66 Бк.
Установим время измерения равным 1 мин. и проведем 7 измерений. Мы, вероятно, получим числа типа: 93, 100 95, 103, 107, 92, 97 и т.д.
Только среднее их значение даст величину, близкую к 100 распадам в минуту, т. е. 1,66 Бк.
Иными словами, для достоверного знания активности необходимо достаточно большое количество измерений.
Слайд 18Промежуточный вывод
1. Для количественного определения загрязнения окружающей среды радионуклидами или их содержания
Промежуточный вывод
1. Для количественного определения загрязнения окружающей среды радионуклидами или их содержания

В то же время величина активности должна быть всегда связана с конкретным названием радионуклида.
Становясь на совершенно формальные позиции, отработанное ядерное топливо или отходы производства, представляющие собой смесь радионуклидов, можно характеризовать суммарной их активностью.
Но суммарная активность не будет нести какой-либо конкретной экологической информации, полезной для определения воздействия, так как каждый радионуклид является источником характерной только для него радиации.
Слайд 192. Что такое Радиоактивность. Термин «радиоактивность» был введен М. Кюри для обозначения
2. Что такое Радиоактивность. Термин «радиоактивность» был введен М. Кюри для обозначения

Атомные ядра можно разбить на две группы: нуклоностабильные и нуклононестабильные.
Испускание α- и β-частиц или γ-квантов, происходит в результате ядерных превращений.
Анализируя эти превращения, можно делать упор на два разных аспекта:
1. На то, что мы имеем превращение одного элемента в другой;
2. На то, что мы имеем дело с переходом нестабильного ядра в более стабильное.
Дадим «окончательное» определение радиоактивности, делая акцент на превращении одного химического элемента в другой. Радиоактивность — это самопроизвольное превращение изотопов одного элемента в изотопы другого, происходящее путем испускания элементарных частиц или ядер. Превращения могут происходить как из основного, так и метастабильного состояния материнского нуклида за время T1/2 > 10-7 с, существенно превышающее время жизни возбужденного составного ядра в ядерных реакциях, происходящих за счет сильных взаимодействий.
Слайд 203. Стабильные и нестабильные ядра. Трудности возникают и при попытке дать определения
3. Стабильные и нестабильные ядра. Трудности возникают и при попытке дать определения

Нижнюю временную границу для периода полураспада определить несложно. Так как в поле нашего рассмотрения находятся только нуклоностабильные ядра, то самые быстрые превращения радионуклидов, представляющих интерес для радиоэкологии, происходят за счет электромагнитных взаимодействий и характеризуются T1/2 > 10-7 с.
В ядерной физике достаточно широкое распространение нашло формальное деление радионуклидов на короткоживущие и долгоживущие. Обычно к короткоживущим относят радионуклиды с периодом полураспада Т1/2 < 10 сут.
Определить верхнюю временную границу для T1/2 и отделить таким образом стабильные нуклиды от радионуклидов трудно. Однозначно это сделать, практически, невозможно. Более того, содержание в Земле 232Th и 238U больше, чем некоторых заведомо стабильных элементов.
Мы не имеем оснований соотносить значение T1/2 со временем существования Солнечной системы, Галактики или Вселенной.
Не очень продуктивным является и утверждение, что радионуклидами являются те нуклиды, для которых известен период полураспада. В этом случае многое определяется экспериментальными возможностями.
Слайд 214. Сколько химических элементов естественного происхождения находится в окружающей нас природной среде.
4. Сколько химических элементов естественного происхождения находится в окружающей нас природной среде.

Сколько стабильных изотопов у этих 81 стабильных элементов? 23 элемента моноизотопны. Рекордсменом по числу стабильных изотопов является олово, у которого их десять. В окружающей нас среде находится 268 стабильных изотопов, из которых 157 являются четно-четными. Нечетно-нечетных изотопов четыре и все они находятся в начале периодической системы: 2H, 6Li, 10B и 14N. Четно-нечетных стабильных нуклидов 54, а нечетно-четных — 52. (268-й нуклид – это водород — 1H, который стоит особняком при такой классификации.)
Радионуклиды с периодами полураспада порядка времени существования Солнечной системы или больше были образованы тогда (а частично и до того), когда возникло вещество, из которого сформировалась Солнечная система.
Эти радионуклиды входившие в состав вещества Солнечной системы являются основным источником естественного радиационного фона и получили название примордиальных. (Primordial – изначальный, исконний. Радионуклидов естественного происхождения много. Так, например, изотопы радия, радона или полония являются основными дозообразующими радионуклидами для человека, но они являются дочерними примордиальных. Во многих случаях это различие полезно иметь ввиду.)
Их делят на радионуклиды, образующие радиоактивные семейства (семейства 232Th, 235U и 238U), и отдельно встречающиеся радионуклиды.
Слайд 22Дошедшие до нашего времени отдельно встречающиеся примордиальные радионуклиды, распадающиеся за счет α-распада,
Дошедшие до нашего времени отдельно встречающиеся примордиальные радионуклиды, распадающиеся за счет α-распада,
Слайд 237·10-8
7·10-8
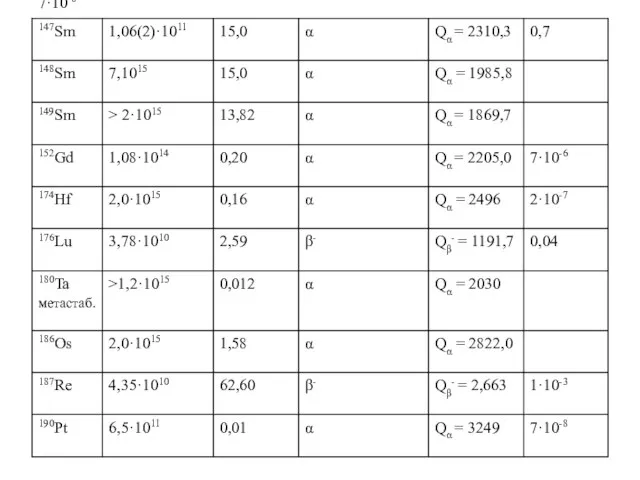
Слайд 24Дочерние продукты распада 232Th, 235U и 238U независимо от их периода полураспада
Дочерние продукты распада 232Th, 235U и 238U независимо от их периода полураспада

Действительно, если принять содержание урана в земной коре равным 1014 тонн, а тория примерно в 5 раз больше, то им сопутствуют ~43 кг франция (в основном 22387Fr от распада 235U) и всего ~22 г астата (в основном 21885At от распада 238U).
«Благодаря» явлению радиоактивности мы оказываемся в состоянии при полной массе земной коры ~2,8·1025 г определить в ней присутствие редкого химического элемента — астата в количестве всего ~22 г, причем с относительной погрешностью, зависящей, в основном, от точности определения содержания 235U и 238U.
На этом пути удалось обнаружить наличие в земной коре еще одного примордиального элемента — плутония. Речь идет об изотопе 244Pu, который концентрируется в редкоземельном минерале бастнасите. Содержание его в земной коре оценивается величиной порядка нескольких грамм.
 Решение задач по кинематике графическим способом
Решение задач по кинематике графическим способом Matech cnc machine
Matech cnc machine Механическое движение. Урок физики в 7 классе
Механическое движение. Урок физики в 7 классе Форма и характеристики электрических сигналов. Анализ
Форма и характеристики электрических сигналов. Анализ Электричество и магнетизм. Электрическое поле в диэлектриках (Лекция 5)
Электричество и магнетизм. Электрическое поле в диэлектриках (Лекция 5) Расчет смесителей
Расчет смесителей Задачи атомной и ядерной физики, астрономии
Задачи атомной и ядерной физики, астрономии Мир в ультрафиолетовых лучах
Мир в ультрафиолетовых лучах Движение тела по окружности с постоянной по модулю скорости
Движение тела по окружности с постоянной по модулю скорости Импульс. Закон сохранения импульса
Импульс. Закон сохранения импульса Физика вокруг нас
Физика вокруг нас Зависимость центростремительной силы от массы, радиуса и угловой скорости
Зависимость центростремительной силы от массы, радиуса и угловой скорости Расчет вакум-насоса
Расчет вакум-насоса Взаимодействие тел
Взаимодействие тел Серво привод с электромеханическим распором
Серво привод с электромеханическим распором Определение температуры. Абсолютная температура
Определение температуры. Абсолютная температура Изменения в технике 2021 модельного года
Изменения в технике 2021 модельного года Индукция магнитного поля
Индукция магнитного поля Закон Ома и удельное сопротивление проводника. Решение задач
Закон Ома и удельное сопротивление проводника. Решение задач Многофункциональная система обслуживания придомовых территорий
Многофункциональная система обслуживания придомовых территорий Биохимическая физика
Биохимическая физика Строение атома
Строение атома Приемы разрешения ТП ГСА
Приемы разрешения ТП ГСА Импульс тела. Закон сохранения импульса тела
Импульс тела. Закон сохранения импульса тела Спектр электромагнитных волн
Спектр электромагнитных волн Кулачковый механизм
Кулачковый механизм Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Презентация Механика Лекция 1
Презентация Механика Лекция 1