Термодинамика высокоэластичной деформации

Способы выражения напряжений и деформаций
Под действием силы Р в образце с поперечным сечением S возникает напряжение f. В Л раз уменьшается поперечное сечение и в Л раз увеличится действующее напряжение.

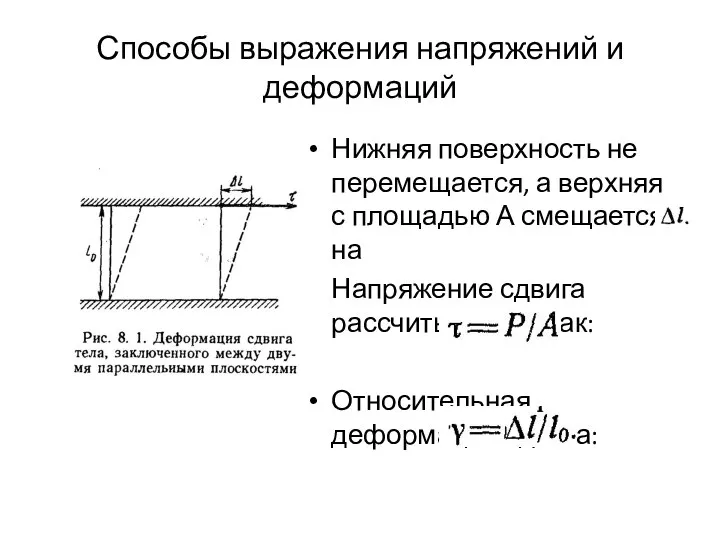
Способы выражения напряжений и деформаций
Нижняя поверхность не перемещается, а верхняя с площадью А смещается на
Напряжение сдвига рассчитывается как:
Относительная деформация сдвига:

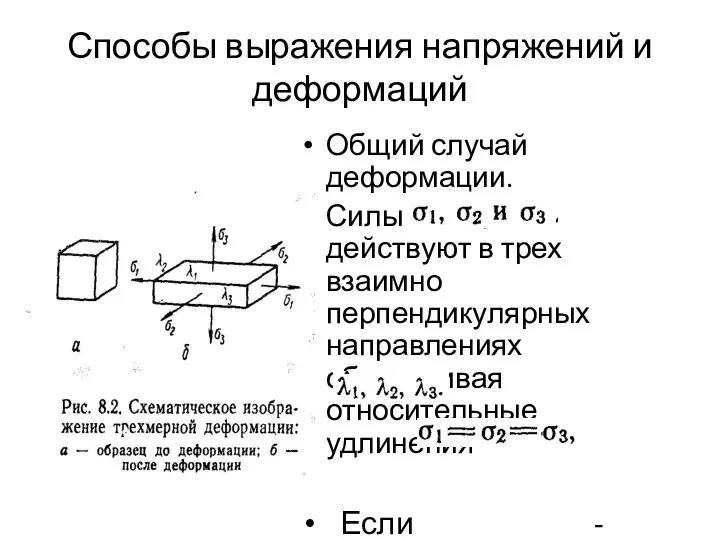
Способы выражения напряжений и деформаций
Общий случай деформации.
Силы действуют в трех взаимно перпендикулярных направлениях обеспечивая относительные удлинения
Если - всестороннее расширение или сжатие.

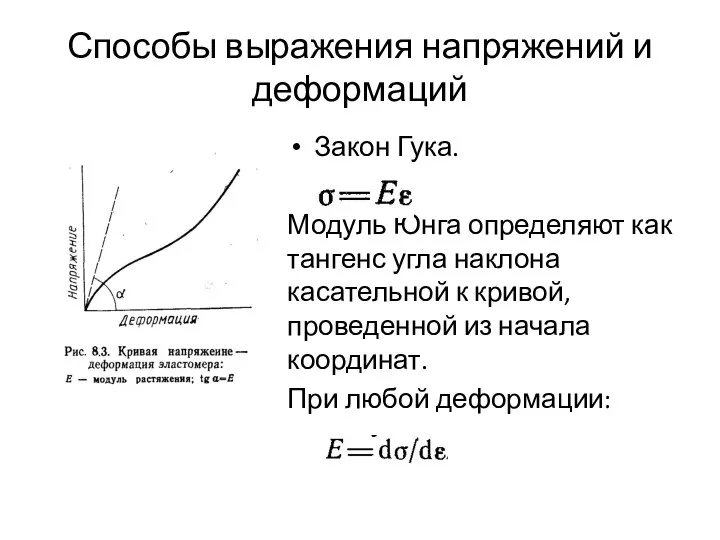
Способы выражения напряжений и деформаций
Закон Гука.
Модуль Юнга определяют как тангенс угла наклона касательной к кривой, проведенной из начала координат.
При любой деформации:

Изменение термодинамических параметров при деформации
Эластомер (полимер в высокоэластичном состоянии) длиной l0 под действием напряжения F удлинится на dl. Исключаем вязкоупругость.
Эластомеры не меняют объема при деформации.
Работа деформации образца обусловлена только действием приложенной силы.

Изменение термодинамических параметров при деформации
По 2 закону термодинамики:
(1)
Внутренняя энергия складывается из теплоты, подведенной к системе, и работы, совершенной над системой.
Деформация образца: (2)
Для равновесного процесса: (3)
Следовательно: (4)

Изменение термодинамических параметров при деформации
Согласно второму закону термодинамики внутренняя энергия системы складывается из свободной и связанной .
(5)
Подставляя (4) в (5), получим:
(6)
При постоянных температуре и объеме образца: (7)

Изменение термодинамических параметров при деформации
Выражение (7) раскрывает физический смысл деформирующей силы: она равна изменению свободной энергии системы в расчете на единицу удлинения.
Определяем из уравнения (5) = -
Подставив в уравнение (7) получим общее выражение для изменения термодинамических параметров эластомера в процессе деформации:
(8)

Изменение термодинамических параметров при деформации
Уравнение (8) можно записать в виде:
Сетчатые эластомеры с малой частотой сетки – при температуре выше Tc ведут себя как идеальные эластомеры ( ) - напряжение, возникающее при деформации обусловлено только изменением энтропии (за счет выпрямления молекулярных клубков при ориентации). Возникновение ориентации приводит к уменьшению энтропии.
(9)

Изменение термодинамических параметров при деформации
При изотермическом сжатии газа (свойства близки к идеальному) давление меняется за счет энтропии:
(10)
Упругость эластомера имеет газовую природу: в идеальном эластомере напряжение при деформации происходит из-за изменения порядка в расположении сегментов, а в идеальном газе из-за изменения порядка в расположении молекул.

Изменение термодинамических параметров при деформации
При малой деформации идеального кристалла (кристаллическая структура не нарушается) напряжение возникает только за счет изменения межатомных расстояний кристаллической решетки, тогда для идеального кристалла:
(11)
Из уравнения (8) можно рассчитать вклад изменения свободной энергии и энтропии в величину напряжения реального эластомера, если известна зависимость напряжения от температуры при разных удлинениях.

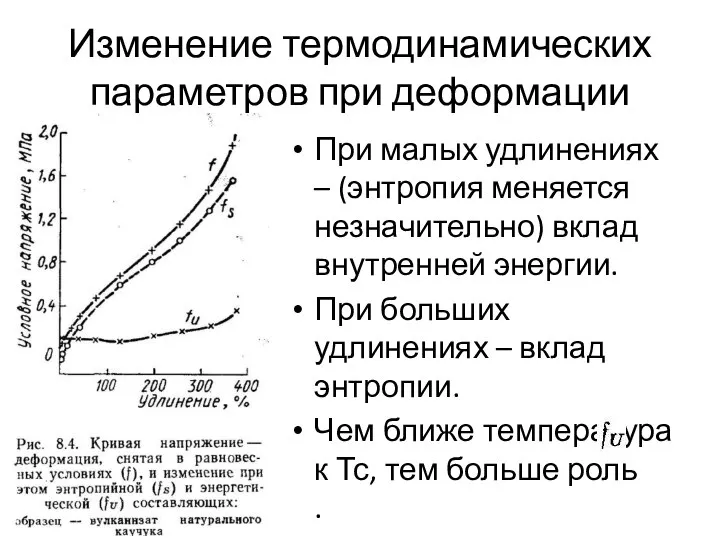
Изменение термодинамических параметров при деформации
При малых удлинениях – (энтропия меняется незначительно) вклад внутренней энергии.
При больших удлинениях – вклад энтропии.
Чем ближе температура к Тс, тем больше роль .

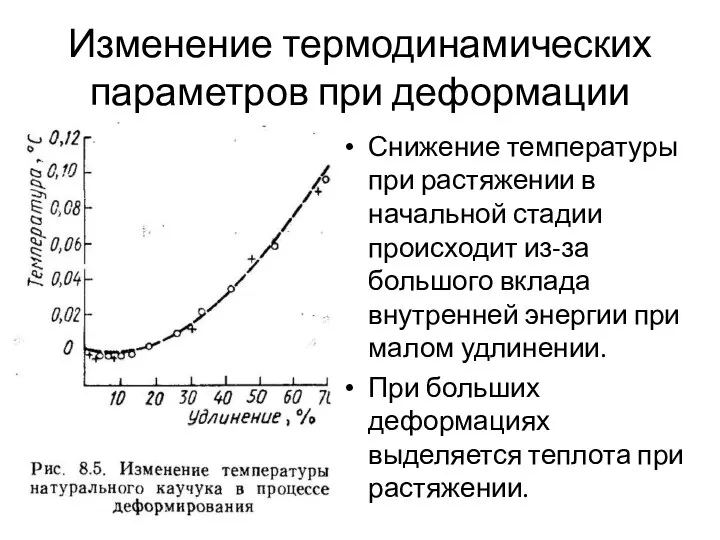
Изменение термодинамических параметров при деформации
Снижение температуры при растяжении в начальной стадии происходит из-за большого вклада внутренней энергии при малом удлинении.
При больших деформациях выделяется теплота при растяжении.

Изменение термодинамических параметров при деформации
В адиабатическом режиме растяжения энтропия системы не меняется – поэтому меняется температура, также как меняется количество теплоты в системе с теплоемкостью в изотермическом процессе:
(12)

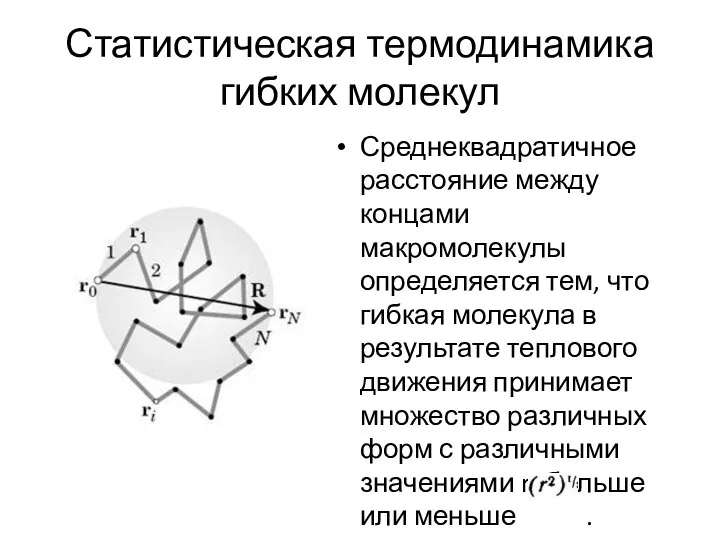
Статистическая термодинамика гибких молекул
Среднеквадратичное расстояние между концами макромолекулы определяется тем, что гибкая молекула в результате теплового движения принимает множество различных форм с различными значениями r (больше или меньше .

Статистическая термодинамика гибких молекул
Считаем, что вращение вокруг простой связи свободно.
При большом числе (n) звеньев C-C в цепи среднеквадратичное расстояние между концами определится как:
(13)
Где l – длина звена, α=180 –ϕ, ϕ – валентный угол.

Статистическая термодинамика гибких молекул
Для молекулы полиэтилена ϕ равен 109,5.
Зная формула (13) упрощается: (14)
Среднеквадратичное расстояние между концами цепи пропорционально корню квадратному из длины цепи, т.е. молекулярной массы.

Статистическая термодинамика гибких молекул
Свободносочлененная цепь – валентный угол не сохраняется, полная свобода вращения каждого последующего звена относительно предыдущего.
Такая цепь более гибкая, и ее размеры меньше, чем у цепи с фиксированным валентным углом. (для полиэтилена в меньше).

Статистическая термодинамика гибких молекул
Для статических расчетов принимают наиболее простую модель. Принимаем, что сегменты жесткие, соединения между ними свободносочлененные.
Подбираем длину сегмента или число сегментов такое, чтобы расстояние было таким же как для реальной молекулы.

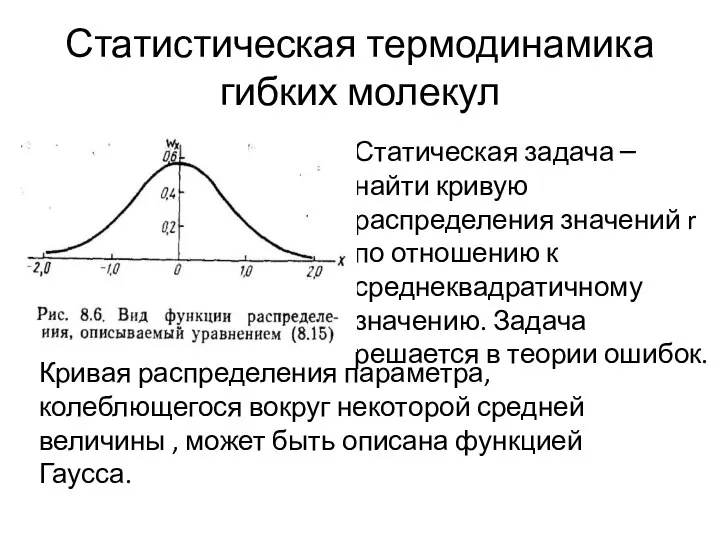
Статистическая термодинамика гибких молекул
Статическая задача – найти кривую распределения значений r по отношению к среднеквадратичному значению. Задача решается в теории ошибок.
Кривая распределения параметра, колеблющегося вокруг некоторой средней величины , может быть описана функцией Гаусса.

Статистическая термодинамика гибких молекул
Пусть каждой длине радиуса-вектора, соединяющего концы макромолекулы, соответствует определенное значение вероятности возникновения данной конформации.
Каждому значению радиуса – вектора r будет соответствовать определенная вероятность Wr. Зависимость Wr oт r описывается функцией Гаусса:
(15)
Где b- константа, принимающая разные значения в зависимости от системы.

Статистическая термодинамика гибких молекул
Для свободносочлененной цепи:
Значение вероятности, расчитанное по формуле (15), относится к единице объема и называется плотностью вероятности.

Статистическая термодинамика гибких молекул
Пусть радиусу-вектору r соответствует плотность вероятности Wr, с увеличением радиуса на dr вероятность новой конформации окажется Wrdr.
Новая величина тем больше, чем больше объем заключенный между сферами r и r+dr.
Объем приближенно равен . Умножим объем на Wr найденный в (15), получим:
(16)

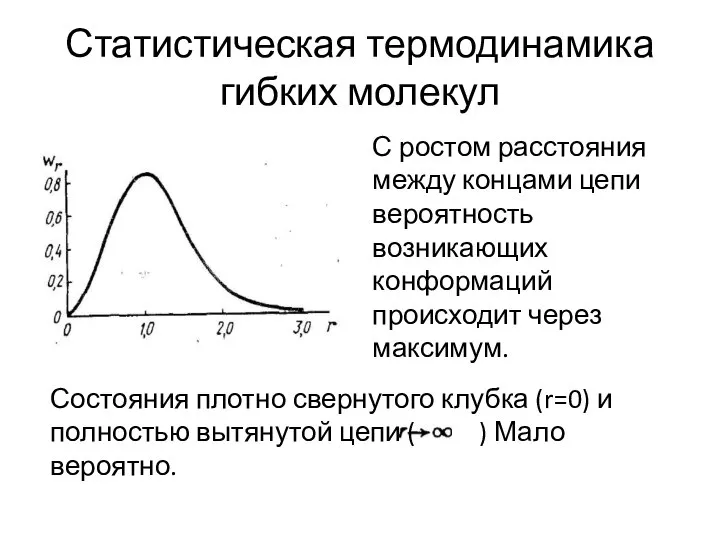
Статистическая термодинамика гибких молекул
С ростом расстояния между концами цепи вероятность возникающих конформаций происходит через максимум.
Состояния плотно свернутого клубка (r=0) и полностью вытянутой цепи ( ) Мало вероятно.

Статистическая термодинамика гибких молекул
Положение максимума определяет наиболее вероятный размер клубка r0:
(17)

Равновесный модуль эластичности
Энтропия системы рассчитывается по формуле Больцмана:
(18)
Подставляя (16) в (18), получим значение энтропии изолированной молекулярной цепи:
(19)
Для идеального эластомера в формулу (9) подставляем (19) и получим:
(20)

Равновесный модуль эластичности
Подставив значение (17) в выражение (20) окончательно получим:
(21)
Уравнение (21) характеризует зависимость напряжения f от относительной деформации r/dr для отдельной макромолекулы.
Уравнение (21) получено только для пространственно- сшитых полимеров (из-за отсутствия вязкотекучей необратимой деформации).

Равновесный модуль эластичности
Модуль эластичности макромолекулы является коэффициентом пропорциональности между напряжением и деформацией: (22)
Модуль эластичности пропорционален абсолютной температуре. В сжатом каучуке сегменты с ростом температуры стремятся вернуть клубок в наиболее вероятное положение.

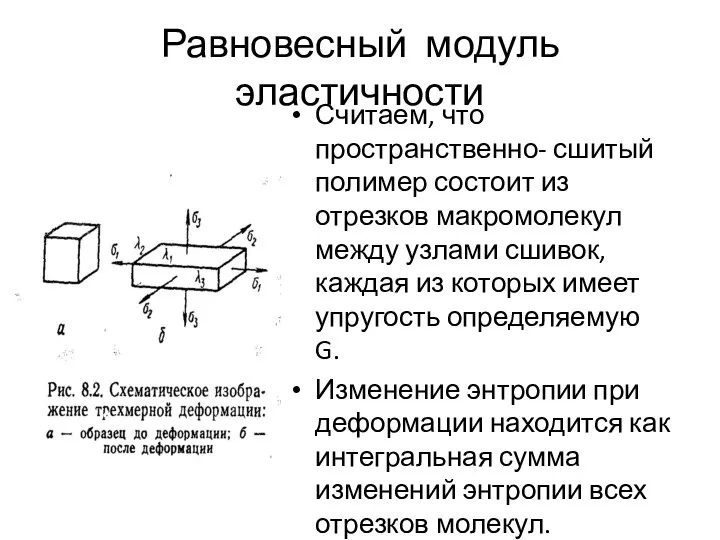
Равновесный модуль эластичности
Считаем, что пространственно- сшитый полимер состоит из отрезков макромолекул между узлами сшивок, каждая из которых имеет упругость определяемую G.
Изменение энтропии при деформации находится как интегральная сумма изменений энтропии всех отрезков молекул.

Равновесный модуль эластичности
Общее изменение энтропии образца, состоящего из N отрезков макромолекул:
(23)
Если внутренняя энергия не меняется и , то по 2 закону термодинамики , тогда работа деформации, равная изменению свободной энергии в единице объема образца с учетом (23) равна:
(24)

Равновесный модуль эластичности
Модуль определен в равновесных условиях, зависит от числа отрезков макромолекул в единице объема и от абсолютной температуры:
(25)
Модули растяжения и сдвига связаны соотношением , поэтому:
(26)

Равновесный модуль эластичности
Частный случай. При одноосном растяжении кубического образца с длиной ребра 1.
Объем образца не меняется, поперечное сечение уменьшается в раз. Каждая сторона уменьшается в , это значит что . Уравнение (24) примет вид:
(27)
Для истинного напряжения:
(28)

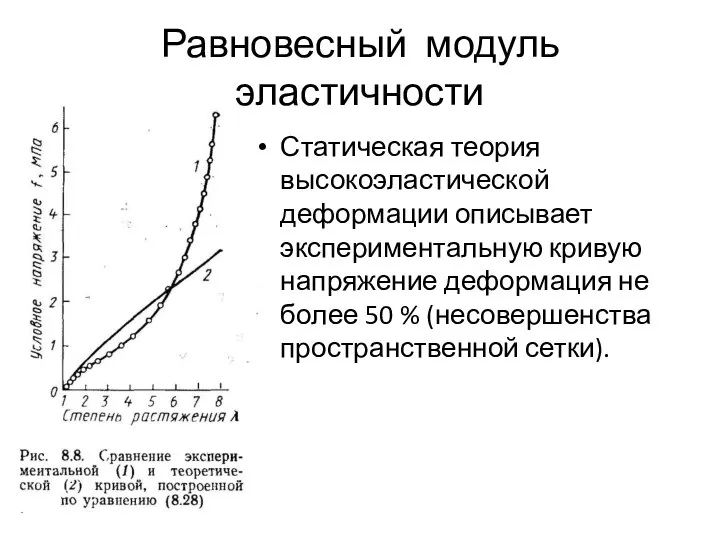
Равновесный модуль эластичности
Статическая теория высокоэластической деформации описывает экспериментальную кривую напряжение деформация не более 50 % (несовершенства пространственной сетки).

Равновесный модуль эластичности
Для экспериментальных данных применима теория Бартенева:
(29)
Теория Муни:
(30)
Сравнивая (30), (27) и (28) получаем: